GUI Final -- Spring 2010

(24 points) Fill in the blanks for each of the following questions:
1. b-spline Which cubic spline does not pass through any of its control points and provides C(0), C(1), and C(2) continuity?
2. interactors The model that divides behaviors into six separate actions called a start action, running action, stop action, abort action, outside action, and back inside action.
3. 4 The number of control points required to define a cubic spline.
4. An interactor is implemented using a set of states and transitions that are collectively called a state machine/finite automata.
5. Bezier Which cubic spline passes through its beginning and ending control points (but not its two intermediate control points) and provides C(0) and C(1) continuity?
6. repaint What Java command allows you to specify a clipping region that should be used by paintComponent?
7. 12 What is the minimum frame rate required to make the human brain think that it is seeing smooth, animated motion?
8. Swing Timer What Java class is it recommended you use if you want to implement an animation?
9. composition The technique to use if you want to inherit an object's implementation, but not its interface.
10. An equation that defines a shape may have either the form F(x,y) = 0, in which case it is called an implicit equation, or it may have the form x(t) = g(t), y(t) = h(t), in which case it is called a parametric equation.
11. convex hull The smallest polygon that will contain all of the control points of a geometric object.
12. If a computer is too slow to provide smooth animation, an animator may create a few highly detailed frames, called key frames, and then have a computer interpolate between the frames using simplifying assumptions, such as linear interpolation or derivatives.
(4 points) For each of the following problems, circle either parametric or implicit to indicate whether the shape's parametric or implicit equation would provide the simplest method for solving the problem (boldfaced answers are the correct answers):
1. parametric implicit Animatatedly moving an object around the boundary of a circle.
2. parametric implicit Finding the distance of a mouse point from a line.
3. parametric implicit Determining whether a mouse point is inside or outside a circle.
4. parametric implicit Finding the nearest point on a cubic spline to a mouse point.
(7 points) Suppose that you have a pre-existing spreadsheet application that runs only on MS Windows. You want to turn the spreadsheet application into a distributed application that will allow a group of people to collaboratively work on the spreadsheet. You also want the distributed application to work with any of the three major OS's (Linux, Windows, Mac). What is the simplest of the 5 distributed models for implementing this distributed application? Why?
The pixel/event distribution model, because it will not require you to modify the spreadsheet application. Instead you can insert software between the application and the input/output system that inserts events from the distributed users into the application's event queue and that captures changes to the application's display and sends the bit changes to each user's machine. This solution will allow the application to appear to work on each of the users' operating systems, while in fact running locally on a Windows box.
(7 points) Suppose that I was implementing a distributed, adversarial, multi-user game. Which of the 5 distributed models would probably be the best choice for implementing this game? Why?
Programmable API: The choices are essentially between the programmable api and the model/data distribution techniques. The pixel/event distribution and graphics package techniques are too slow for an adversarial game, because they require too much network traffic. The important thing about an adversarial game setting is that competitors be on equal footing and that competitors all see the same game state at the same time. The model/data distribution technique fails for both of these reasons: 1) if the game is a game of speed, then a local user will have an unfair advantage over remote users, and 2) it could be devastating to a player to have their game state rolled back by a collaboration server, thus allowing other players whose state was not rolled back to get way ahead of them. The programmable api is the fairest, because even though the game state may change a bit slower for each user, at least each user will be on roughly equal footing and every user will see the same game state at all times.
(5 points) Why does XOR allow me to draw and erase a single object without having to redraw the rest of the display?
When you XOR the same bits twice to the same area of the screen, it returns the screen to its original state. Thus if you use XOR to draw an object twice in the same place, the second draw will erase the object from the screen, leaving the screen in its original state.
(10 points) For each of the following display situations, indicate whether you would use xor, clipping(#), or total redraw to redraw the display. If you would use clipping, indicate how many bounding boxes you would use.
1. xor I am moving a feedback object around the display and nothing else in the display is changing.
2. total redraw I have a boxes-and-arrows display that will typically have about 20 boxes and 50 arrows.
3. clipping(1) I have a circuit diagram that may require anywhere from 10,000-1,000,000 gates and I want to redraw the diagram after moving a collection of 30 adjacent, and closely co-located, gates by 20 pixels to the right. Because the gates moved by such a small amount relative to the size of the moved collection of gates, the difference between the old and new bounding boxes is small, and the two should be merged.
4. I have a tiled gameboard that measures 10000x10000 tiles with characters that move from tile to tile. The tiles do not overlap and the display is large enough for the user to see a 100x100 subset of the tiles. Consider each of the following scenarios:
  1. xor A character moves from one visible tile to a horizontally adjacent and also visible tile
  2. clipping(1) A character moves horizontally by one tile, and in doing so, forces 5 new columns of tile to be scrolled onto the right side of the screen and 5 old columns of tile to be scrolled off the left side of the screen. The entire visible portion of the screen is going to change, not just the 5 leftmost columns and the 5 rightmost columns, so you should use one bounding box that is equal in size to the entire screen.
(10 points) For each of the following scenarios, indicate which of the following interactor types would best handle that scenario:
- Choice interactor
- Rotate interactor
- Move/Resize interactor
- Sketch interactor
- Text edit interactor
- New object interactor
1. Rotate interactor Move the hour hand of a clock.
2. New object interactor or Move/Resize interactor Sweep out a rectangle and select all the objects that intersect this rectangle
3. Choice interactor Select a single object on the display and deselect whatever object was previously selected
4. Choice interactor Implement the up/down arrow buttons in a scroll bar
5. Move interactor Implement the slider box in a scroll bar
(6 points) If you are trying to design an interface that will enhance a user's productivity, will placing several simultaneous, unrelated animations around the display typically improve or diminish a user's productivity? Why?
It will hurt most user's productivity, because their eye will want to constantly move around the screen, scanning each animation in turn. If the user allows their eye to move, that will force context switches which will inhibit the user's productivity. The user may be able to force their eye to stay on one animation or one task, but the cognitive effort required to force their eye to stay on one fixed point of the screen will detract from the cognitive activity that can be applied to the task and hence will inhibit the user's productivity.
(7 points) Suppose I want to animatedly move an object in a straight line from the point (30,50) to the point (110, 200). Show me the equations I should use to do the animation as a function of time t, where t will vary from 0 to 1. x(t) = 30 + (110-30)t = 30 + 80t y(t) = 50 + (200-50)t = 50 + 150t

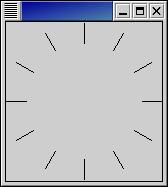
(20 points) Write a Java paintComponent method that uses a Java Graphics2D object and Java2D transforms to draw the following picture of the 12 hours of a clock:

To receive full credit your answer must use only one instance of a Java2D line and must use transforms.

You should make the following assumptions:

The length of the tickmarks is stored in a variable called length.
Either the tickmarks at 3:00 and 9:00 or the tickmarks at 12:00 and 6:00 should touch the side of the panel, depending on which of the two dimensions of the panel is shorter.
The figure is centered in the Java panel.

Do not show me any code other than the paintComponent method. Here is the beginning of the code:

public void paintComponent(Graphics g) {
    super.paintComponent(g);

    // work on a copy of the graphics context
    Graphics2D g2 = (Graphics2D)g.create();
    // set up the dash in its own coordinate system
    Line2D tickmark = new Line2D.Double(0, 0, length, 0);


    // get the width and height of the panel so that I can center the clock
    int width = getWidth();
    int height = getHeight();

    // the innerRadius is the distance of the invisible line from the center
    // of the clock to the beginning of the tick mark
    double innerRadius = Math.min(width, height) / 2 - length;

    // move the clock back to the center--remember that transformations
    // are applied in the reverse order in which they are added to the
    // transform, so this will be the last transform actually applied
    g2.translate(width / 2, height / 2);

    // There are two PI radians in a circle divided by 12 increments
    double rotateIncrement = (2*Math.PI) / 12;

    for (int i = 0; i < 12; i++) {
        g2.rotate(rotateIncrement);

        // translate the line to its proper location
        g2.translate(innerRadius, 0);  
        g2.draw(tickmark);

        // translate the line back to the center so that the rotate
        // transformation works properly in the next step
        g2.translate(-innerRadius, 0);
     }
     
    g2.dispose();
}/b>