




Next: Positive Definite
Up: Generalized Hermitian Eigenvalue Problems
Previous: Jacobi-Davidson Methods G. Sleijpen and
Contents
Index
Stability and Accuracy Assessments
Z. Bai and R. Li
The generalized eigenvalue problem for a Hermitian matrix pair 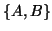 with one of
with one of 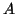 and
and 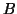 , or some linear combination of
, or some linear combination of 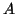 and
and 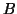 , being
positive definite takes a unique position among all
generalized eigenvalue problems for matrix pairs
because it resembles in many ways the standard Hermitian eigenvalue
problem discussed in Chapter 4.
Matrix pairs as such are called Hermitian definite pairs.
We shall consider separately
, being
positive definite takes a unique position among all
generalized eigenvalue problems for matrix pairs
because it resembles in many ways the standard Hermitian eigenvalue
problem discussed in Chapter 4.
Matrix pairs as such are called Hermitian definite pairs.
We shall consider separately
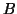 is definite and well-conditioned, meaning that
is definite and well-conditioned, meaning that
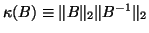 is not too
large.
is not too
large.![[*]](http://www.netlib.org/utk/icons/footnote.png)
- Some combination of
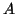 and
and 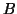 is definite and
well-conditioned.
is definite and
well-conditioned.
In this section, we only review some basic results that
are readily applicable to assess how accurate computed
eigenvalues and eigenvectors may be. We assume
the availability of residual vectors which are usually available
upon the exit of a successful computation. If not, they can be
computed at marginal cost afterwards.
For the treatment of error estimation of computed eigenvalues and
eigenvectors of dense generalized Hermitian eigenproblems,
see Chapter 4 of the LAPACK Users' Guide [12].
Subsections





Next: Positive Definite
Up: Generalized Hermitian Eigenvalue Problems
Previous: Jacobi-Davidson Methods G. Sleijpen and
Contents
Index
Susan Blackford
2000-11-20
![]() with one of
with one of ![]() and
and ![]() , or some linear combination of
, or some linear combination of ![]() and
and ![]() , being
positive definite takes a unique position among all
generalized eigenvalue problems for matrix pairs
because it resembles in many ways the standard Hermitian eigenvalue
problem discussed in Chapter 4.
Matrix pairs as such are called Hermitian definite pairs.
We shall consider separately
, being
positive definite takes a unique position among all
generalized eigenvalue problems for matrix pairs
because it resembles in many ways the standard Hermitian eigenvalue
problem discussed in Chapter 4.
Matrix pairs as such are called Hermitian definite pairs.
We shall consider separately