Perhaps the most successful numerical algorithm for
computing the complete eigensystem of a general square matrix ![]() is the implicitly shifted QR algorithm. One of the keys to the
success of this method is its relationship to the
Schur decomposition
is the implicitly shifted QR algorithm. One of the keys to the
success of this method is its relationship to the
Schur decomposition
The QR algorithm
produces a sequence of unitary similarity transformations
that iteratively reduce ![]() to upper triangular form
(see §7.3).
In other words, it
computes a Schur decomposition. A practical implementation of the
QR algorithm begins
with an initial unitary similarity transformation of
to upper triangular form
(see §7.3).
In other words, it
computes a Schur decomposition. A practical implementation of the
QR algorithm begins
with an initial unitary similarity transformation of ![]() to the condensed
form
to the condensed
form
![]() where
where ![]() is upper Hessenberg (``almost upper triangular'')
and
is upper Hessenberg (``almost upper triangular'')
and ![]() is unitary. Then the following iteration is performed.
is unitary. Then the following iteration is performed.
SHIFTED QR METHOD
factor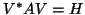
foruntil convergence
select a shift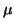
QR-factorize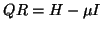
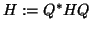
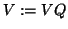
end for
In this scheme, ![]() is unitary and
is unitary and ![]() is upper
triangular (i.e., the QR factorization of
is upper
triangular (i.e., the QR factorization of ![]() ).
It is easy to see that
).
It is easy to see that ![]() is unitarily similar to
is unitarily similar to ![]() throughout the course of this iteration. The iteration is continued until
the subdiagonal elements of
throughout the course of this iteration. The iteration is continued until
the subdiagonal elements of ![]() converge to zero, i.e., until a Schur
decomposition has been (approximately) obtained.
converge to zero, i.e., until a Schur
decomposition has been (approximately) obtained.
If ![]() represents the leading
represents the leading ![]() columns of
columns of ![]() , and
, and ![]() the
leading principal
the
leading principal ![]() submatrix of
submatrix of ![]() in (7.11),
then
in (7.11),
then
We are going to exploit this aspect of the Schur decomposition.
We shall also exploit
the fact that a variant of the QR iteration can be devised that will force
eigenvalues of interest to appear in this leading ![]() block of
block of ![]() as the iteration proceeds.
Our goal will be to develop a truncated form of the QR
method that is suitable for computing a selected set of
as the iteration proceeds.
Our goal will be to develop a truncated form of the QR
method that is suitable for computing a selected set of ![]() eigenvalues
of a large matrix
eigenvalues
of a large matrix ![]() .
We call implicitly restarted Arnoldi method the IRAM.
.
We call implicitly restarted Arnoldi method the IRAM.