The symmetry of ![]() and
and ![]() is purely an algebraic property and is
not sufficient to ensure any of the special
mathematical properties enjoyed by a definite matrix pencil, such
as those discussed in §2.3.
In fact, it can be shown that any real square matrix
is purely an algebraic property and is
not sufficient to ensure any of the special
mathematical properties enjoyed by a definite matrix pencil, such
as those discussed in §2.3.
In fact, it can be shown that any real square matrix ![]() may be written
as
may be written
as ![]() or
or ![]() , where
, where ![]() and
and ![]() are suitable
symmetric matrices; for example, see [353].
are suitable
symmetric matrices; for example, see [353].
The eigenvalues of a definite matrix pencil are all real,
but an indefinite pencil
may have complex eigenvalues. For example, when
In §2.3, we know that
when ![]() is positive definite we can find a matrix of eigenvectors
is positive definite we can find a matrix of eigenvectors
![]() and a diagonal matrix of eigenvalues
and a diagonal matrix of eigenvalues ![]() such that
such that
![]() with
with ![]() . The
. The ![]() inner product
inner product ![]() forms a true
inner product and
forms a true
inner product and ![]() is a norm.
is a norm.
When ![]() is indefinite and nonsingular
and if
is indefinite and nonsingular
and if ![]() is not defective (i.e., no eigenvectors are missing),
we can find a full set of eigenvectors,
is not defective (i.e., no eigenvectors are missing),
we can find a full set of eigenvectors, ![]() . The equation
. The equation
![]() still holds, and the eigenvectors can be chosen so that
still holds, and the eigenvectors can be chosen so that
![]() , where
, where ![]() is a diagonal matrix with
is a diagonal matrix with ![]() and
and ![]() on the diagonal
(note that it is transpose, not conjugate transpose,
even though some vectors can be complex).
The
on the diagonal
(note that it is transpose, not conjugate transpose,
even though some vectors can be complex).
The ![]() inner product
inner product ![]() is an indefinite inner product or
pseudo-inner product, and
is an indefinite inner product or
pseudo-inner product, and ![]() can be used for normalizing purposes. Unlike the positive definite case, there
is a set of vectors having pseudolength zero (as measured by
can be used for normalizing purposes. Unlike the positive definite case, there
is a set of vectors having pseudolength zero (as measured by ![]() ).
In fact, it is possible for an eigenvector
).
In fact, it is possible for an eigenvector ![]() to satisfy
to satisfy
![]() . This implies that the Rayleigh quotient
. This implies that the Rayleigh quotient
The analogy between the definite and the indefinite cases
can be taken further. When ![]() is positive definite,
is positive definite, ![]() is an approximate
eigenvector, and
is an approximate
eigenvector, and ![]() is an approximate eigenvalue, we have the standard
residual bound:
is an approximate eigenvalue, we have the standard
residual bound:
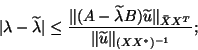
If both ![]() and
and ![]() are singular,
or close to singular, worse problems may occur.
Assume that there is a
nonzero vector
are singular,
or close to singular, worse problems may occur.
Assume that there is a
nonzero vector ![]() such that
such that ![]() ; then any complex number
; then any complex number
![]() is an eigenvalue.
A more general case is illustrated in the example
below:
is an eigenvalue.
A more general case is illustrated in the example
below:
![\begin{displaymath}
A=\left[\begin{array}{ccc}
1 & 0 & 0\\
0 & -1 & 0\\
0 ...
...}
1 & 0 & 1\\
0 & -1 & 1\\
1 & 1 & 0
\end{array}\right].
\end{displaymath}](img2883.png)
In practice, if
we have a singular pencil, ![]() is singular for any
is singular for any ![]() ,
and a good LU factorization routine should give a warning (when used
in (a) and (b) in the following §8.6.2).
Another sign of a singular pencil is that the eigenvalue routine produces
some random eigenvalues at each run on the same problem.
,
and a good LU factorization routine should give a warning (when used
in (a) and (b) in the following §8.6.2).
Another sign of a singular pencil is that the eigenvalue routine produces
some random eigenvalues at each run on the same problem.