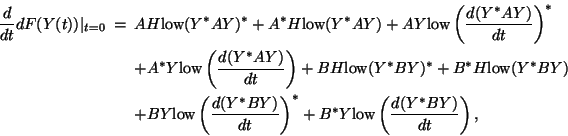Consider two matrices ![]() and
and ![]() which in the absence of error have
the same Schur vectors; i.e., there is a
which in the absence of error have
the same Schur vectors; i.e., there is a
![]() such
that
such
that ![]() and
and ![]() are both block upper triangular
where
are both block upper triangular
where ![]() is the set of
is the set of ![]() by
by ![]() orthogonal matrices.
Now suppose that
orthogonal matrices.
Now suppose that ![]() and
and ![]() are somewhat noisy from measurement errors or
some other kind of lossy filtering.
In that case the
are somewhat noisy from measurement errors or
some other kind of lossy filtering.
In that case the ![]() that upper triangularizes
that upper triangularizes ![]() might not
upper triangularize
might not
upper triangularize ![]() as well. How does one find the best
as well. How does one find the best ![]() ?
?
This is a problem that was presented to us by Schilders
[396], who phrased it as a least squares minimization of
![]() , where
, where
![]() is a mask returning the block lower triangular part of
is a mask returning the block lower triangular part of ![]() ,
where
,
where ![]() is broken up into
is broken up into ![]() blocks.
blocks.
For this problem the differential is a bit tricky and its derivation instructive:
![\begin{eqnarray*}
\tr(V^* dF(Y)) &=& \tr( \mbox{low}(Y^*AY)^*\mbox{low}(Y^*AV + ...
... \\
[1.5pt]
&& + BY\mbox{low}(Y^*BY)^*+B^*Y\mbox{low}(Y^*BY),
\end{eqnarray*}](img3460.png)
With second derivatives given by