CS302 Lecture Notes

CS302 Lecture Notes - Network Flow

Lecture 1: Augmenting Paths, Minimum Cuts, A Pathelogical Example

James S. Plank
Original Notes: April 2, 2008.
Major Overhaul: November, 2014.
Directory: /home/plank/cs302/Notes/Netflow-All

Reference Material

The best description that I have found of the basics of network flow come from a topcoder tutorial, which is available here. I used to make this the required reading for Network Flow, but I have now written my own lecture notes. Still, reading this is a great way to reinforce your knowledge.

There is more material in the following Wikipedia pages. As with a lot of Wikipedia, the presentation is too dry and mathematical, so I don't require that you read it, but I provide links to it anyway:

The Problem

You have a directed graph with non-negative edge weights. The weights of the edges are called capacities. The easiest way to think of them is as pipes that hold water, and each edge capacity represents the volume of water that can flow through the pipe per unit time. Nodes are junctions between multiple pipes.

There are two special nodes, called the source and the sink You assume that there is an infinite source of water at the source. The Network Flow problem is as follows: What is the maximum volume of water that can flow from the source to the sink per unit time? No edge can hold more flow than its capacity, and the amount of flow going into a node has to equal the amount of flow going out of a node.

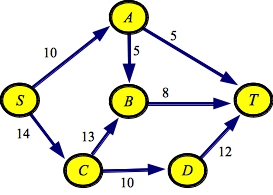
Here's an example graph, with source S and sink T (in this and other pictures, you can click on the pictures, and get the full size picture):

It's not hard to eyeball this graph, and determine that the maximum flow is 23. Here's a graph that shows this flow, subject to the above rules:

A Related Problem: The Minimum Cut

A cut of a graph is a collection of edges that disconnects the source and the sink. A minimum cut is a cut with the smallest total capacity. If the maximum flow through a network is f, then the minimum cut has a total capacity of f. For example, in the above graph, the edges AT, BT and CD compose a minimum cut. I'll show you an algorithm for determining the minimum cut later in this lecture.

Why do we care about this problem?

Network flow problems arise in a variety of ways, some expected and some unexpected. Many logistical applications map clearly to network flow (think about this the next time you try to exit Neyland Stadium after a UT game). Many surprising applications also arise -- you'll see this in your lab.

A Tempting, but Incorrect Solution to Network Flow

Our solution to this problem is going to take the following form: We are going to find a path through the graph that has some flow. Then we are going to remove the flow from the graph and try again. How we "remove the flow" will be the important part of the solution. Before I show you that, let's try a naive approach: Every time we find a path through the graph, we remove the maximum flow through that path from the graph.

Let's try this on the example above. Below, I'll show three pictures: The first removes five units of flow from the path S-A-T, then eight units of flow from the path S-C-B-T, and finally six units of flow from the path S-C-D-T:

Remove 5 units of flow from S-A-T:

Remove 8 units of flow from S-C-B-T:

Remove 6 units of flow from S-C-D-T:

You'll note that the source is no longer connected to the sink, so we can't find any more paths with flow. But we've only found 19 units of flow, and not 23. In other words, our algorithm doesn't work.

The Correct Solution - The Ford-Fulkerson (Augmenting Paths) Algorithm

The problem with our solution is how we removed the flow from the graph. The correct way to do this is called the ``Ford-Fulkerson'' algorithm, and sometimes it is referred to as simply an ``Augmenting Path'' algorithm. The algorithm works as follows:

We are going to maintain three graphs -- a copy of the original graph, a ``flow'' graph, which keeps track of the flow that we discover through the graph, and a ``residual'' graph, which keeps of track of the potential flow that is left in the graph.
The flow graph starts empty, and the residual graph starts out equaling the original.
At each step, we start by finding a path from the source to the sink in the residual graph, that has some flow. If we can't find such a path, we're done.
We add the flow along the path to the flow graph. If there is already flow in the reverse direction, you subtract from that flow first, before adding additional flow to the graph.
We subtract the flow along the path in the residual graph.
We traverse the path backward, from the sink to the source, adding the flow along that path in the backward direction. I typically call this ``adding reverse flow.''

Let's go back to our example above. Below is the starting state of the flow graph and the residual graph:

Flow Graph

Residual Graph

Like before, we start with the path S-A-T. It has a flow of 5. So, we'll add that path to the flow graph, subtract the flow from S-A-T, and also add ``reverse'' flow along the path T-A-S. Here is the result. I'm drawing the ``reverse'' flow in red, since this flow is usually the one that confuses students.

Flow Graph

Residual Graph

Also like before, let's choose our next path to be S-C-B-T, with a flow of 8. We'll add it to the flow graph, subtract it from the residual, and add the reverse flow to the residual:

Flow Graph

Residual Graph

Also like before, let's choose our third path to be S-C-D-T, with a flow of 6. We'll add it to the flow graph, subtract it from the residual, and add the reverse flow to the residual:

Flow Graph

Residual Graph

You'll recall that this is the point at which we were stuck above. However, the reverse edges have now given us another path through the graph: S-A-B-C-D-T, with a flow of four. Let's process those:

Flow Graph

Residual Graph

Now, there's no way to get from the source to the sink in the residual graph. Therefore, our final network flow is 23 units.

Again, we call this the ``Ford-Fulkerson'' algorithm. You'll note that it does not specify how we find the augmenting paths. That will be an important problem that we will address later.

Using the Residual Graph to find the Minimum Cut

To find the minimum cut, you first find all of the nodes that are reachable from the source in the residual graph. Lets color those nodes red, and all of the other nodes green, both in the residual graph and in the original graph:

Residual Graph

Original Graph

The minimum cut is composed of all edges in the original graph, from the red set to the green set. These are highlighted in orange above: AT, BT and CD.

A pathological example of why you need a smart path-finding algorithm

This is a classic example of why you need to have a smart algorithm for finding each augmenting path. Behold the following graph:

It's pretty easy to eyeball this graph and see that it has a maximum flow of 1000. The two paths are S->A->T and S->B->T. However, if you try to determine the maximum flow using augmenting paths, and you choose the wrong path at each step, it will take 1000 iterations of the algorithm. To illustrate, suppose that the first path you choose is S->A->B->T with a flow of one. When you process this path through the residual graph, you end up with the following:

At the next iteration, suppose you choose the path S->B->A->T, again with a flow of one. The residual looks as follows:

You continue in that vein. The pictures below show how you choose S->A->B->T again, and then S->B->A->T, again:

Each time, you add one unit of flow, which means that this will take 1000 iterations. Although this example is unlikely to happen in practice, it demonstrates a need for a smart determination of paths.