 |
It addresses the problem of set similarity. In other words, you have two sets of elements. How similar are they? The metric of similarity is the Jaccard similarity coefficient. This is a very natural metric, defined as follows:
| Jaccard similarity of sets A and B equals |A ∩ B| / |A ∪ B|. |
Think about this for a minute. If two sets are identical, then their Jaccard similarity is one. If they are completely disjoint, then their Jaccard similarity is zero. If set A is twice the size of set B and contains set B completely, then the two sets' Jaccard similarity is 0.5. The same is true if the two sets are the same size, and share exactly two thirds of their elements.
If we like Jaccard similarity as a metric, then think about how you can calculate it. In this discussion, let's assume that A and B are the same size. A straightforward way is to store all of the values of A in a C++ set, and then look up each value of B. That will let you calculate |A ∩ B| and |A ∪ B|, and then you can calculate the Jaccard similarity. What's the running time of that? Our favorite: O(n log(n)), where |A| = |B| = n. The space complexity is O(n), because the size of a tree is proportional to the number of nodes.
If the elements of A and B are large, we can hash them. Since O(n log(n)) is pretty fast, why would we need to improve it? Well, for the same reason as a Bloom Filter -- when they get really big, you start running out of time and space. So a heuristic is nice.
Think about an example. If A and B are identical, then their minimum hashes will clearly be the same. If they are disjoint, and we assume no hash collisions (which I'm going to assume for the remainder of this writeup), then their minimum hashes will clearly be different. Let's take the example where A contains B and is twice its size. Then it is pretty intuitive that the minimum hash of B has a 50% chance of being the minimum hash of A. That's nice.
How about the fourth example -- A and B are the same size and contain 2/3 the same elements. In that case, their Jaccard similarity is 0.5. Let's look at an example:
There are four total elements, and when we hash them, each of the four has an equal probability (0.25) of being the minimum. When 1 or 4 is the minimum, then the two sets will have different minimum hashes. When 2 or 3 is the minimum, then the two sets will have the same minimum hashes. It works!
It's not hard to prove in general -- there are |A ∪ B| total elements, so there are |A ∪ B| total hashes. The minimum hash is a random element chosen from the |A ∪ B| hashes, so it has a probability of:
of being part of the intersection of the two sets. Again -- elegant.
Unfortunately, in order to approximate a probability from a sample drawn from that probability, we need a lot of samples. So, with this version of MinHash, you calculate k different hashes of each value of A and B. For each hash, you compare the minimum values, and from that you approximate the probability. The running time of this is O(nk) so if k is small, then this will be a win. It is also O(1) in terms of space, which is attractive. However, Wikipedia tells us that the error in this technique is 1/sqrt(k). So, for 10% error, you need 100 hash functions. For 1% error, you need 10,000 hash functions. Yick. That's friggin expensive, and if that's all there were to MinHash, I'd simply go with the O(n log(n)) algorithm. Or maybe even use a Bloom Filter! But, there's more, so keep reading.
This version of MinHash has an additional desirable property -- as k approaches n, the accuracy approaches 1, and when k ≥ n, the accuracy is one. That is not true for the k-hash function version of MinHash.
What about the false positives? Believe it or not, they can help you and not hurt you! Let's consider an example that we're going to see below. Two very large sets have 90% of their elements in common. Their Jaccard similarity is thus 90/110 = 0.818182. Suppose we use a Bloom filter where m = 10n and k = 7. Our predicted false positive rate will be 0.0082 (please see the Bloom Filter lecture notes for an explanation).
How does that impact the error of the Jaccard similarity calculation? Let's do a concrete example where A and B both contain 1,000,000 elements, with 900,000 of them being shared. We have put all of the elements of A into the Bloom Filter. Now we test every eleemnt of B. In that test, 900,000 of the elements will return a true positive. 820 of the remaining 100,000 elements will return a false positive. The remaining 99,180 elements will return a true negative. We can leverage the fact that we can estimate the false positive rate to calculate the true Jaccard similarity:
| Technique | Time Complexity | Space Complexity | Accuracy |
| Direct calculation using sets | O(m2n log(n)) | O(mn) | Perfect |
| Direct calculation using sorted vectors | O(mn log(n) + m2n) | O(mn) | Perfect |
| MinHash with k hash functions | O(mnk + m2k) | O(mk) | Error is 1/sqrt(k) |
| MinHash with one hash function | O(mn log(k) + m2k) | O(mk) | Error is 1/sqrt(k) |
| Bloom Filters | O(mnk + m2n) | O(mn) | Error is really small. |
I'm going to project that for this problem, you'll quantify solutions as follows:
For each paper, I added every word of the paper's title, that was 5 letters or longer, to the professor's set. I didn't do anything smart, like remove plurals. I simply used the words (lower case, of course). So, for example, I had words like "erasure" "checkpointing" and "neuromorphic" that are indicative of my research career. I also had words like "approach", "impact" and "effect", which are less distinctive. The words for each professor is in the directory Words:
All of these data sets are relatively small. Here's a histogram, including Miller, Yaakobi and Tarjan:
 |
So, I calculated the Jaccard similarity for each pair of professors in the data set using a shell script (see below). And from that, I generated a heat map for similarity:
 |
You can see some similar pairs of professors there: Me and Dr. Beck, Dr. (F) Li and Dr. Tomsovic, Dr. Costinett and Dr. Tolbert, and Dr. Islam and Dr. McFarlane. You can also see that Drs. Jantz, Schuard and Day are not overly similar to anyone, because they don't have very many publications yet.
UNIX> wc Names/* 1000000 1000000 16098423 Names/01.txt 1000000 1000000 16089116 Names/02.txt 1000000 1000000 16079936 Names/03.txt 3000000 3000000 48267475 total UNIX>Each has a million unique names. 90% of the names in 01.txt are in 02.txt, and 90% of the names in 02.txt are in 03.txt. This will be a good stress-test for the programs.
Here's the bottom line of my implementations:
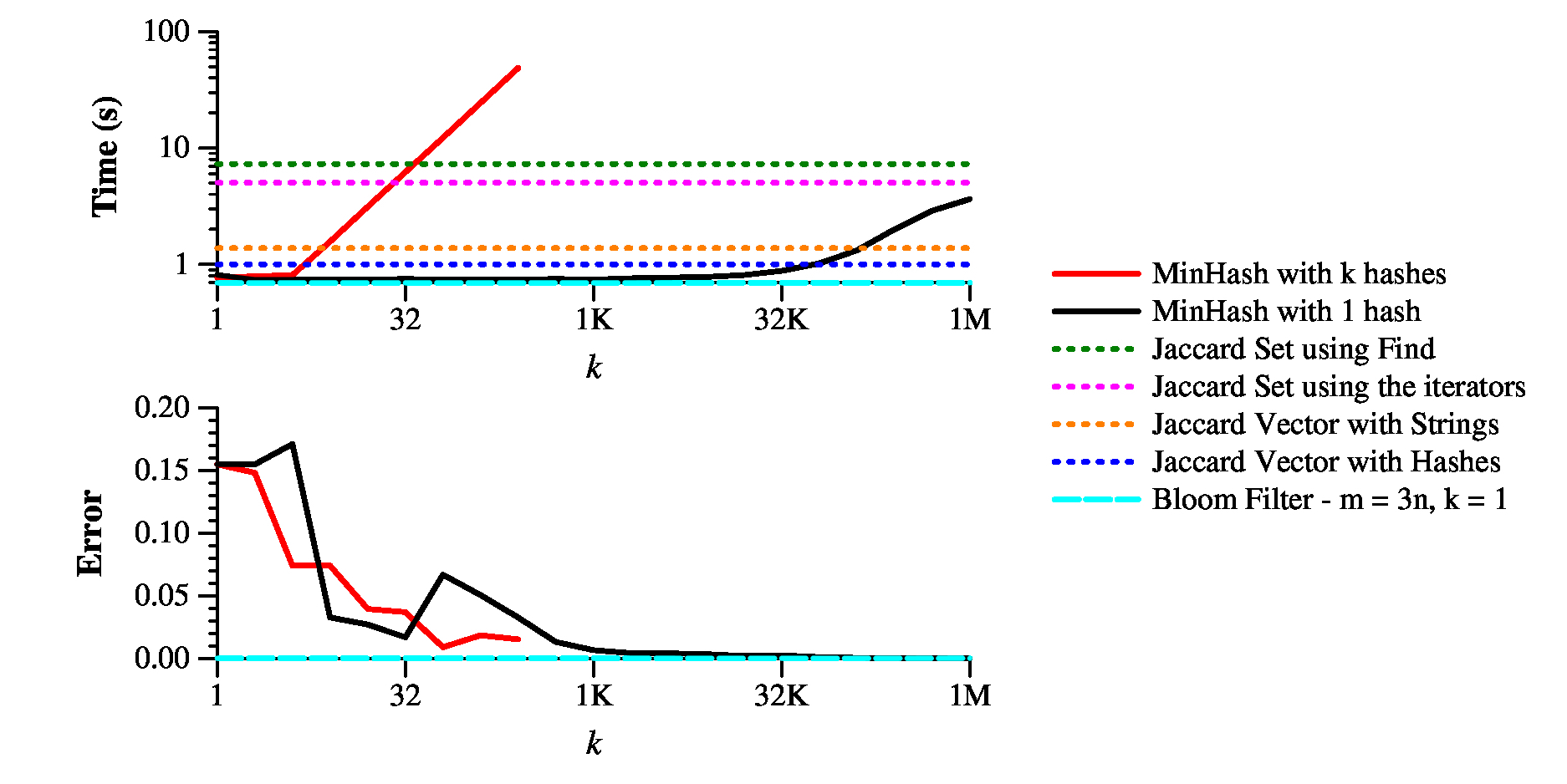 |
As you can see, you can make the direct calculation of Jaccard similarity pretty fast; however, the 1-hash version of MinHash is significantly faster up to k=10K or so, which gets you under 1% error. The k-hash version of MinHash is completely useless.
What about the Bloom Filter? Its performance depends on the settings of k and m. When you use the "recommended" settings of m = 10n and k=7, you get speed that is on par with "Jaccard Vector With Strings." In other words, not useful. On the flip side, the error is incredibly low -- 0.00026. Remember, the false positive rate is not the error, but it is leveraged to predict false positive and hone the error.
So, maybe we can get away with smaller values of m and k. Below is a graph where I plot time and error for various settings of m and k:
 |
As you can see, the performance of pretty much all values of m are similar when k ≤ 4. Why would that be? Well, we can get all four hashes from one call to MD5(). The error is incredibly low -- you'd need k=1,000,000 for min-hash to get that low, and that's the number of items in the sets!
For that reason, in the overall performance graph above, I use m = 3n and k = 1.
Conclusion: Bloom Filters 1, Min-Hash 0.
if [ $# -ne 2 ]; then
echo 'usage: sh minhash.sh f1 f2' >&2
exit 1
fi
total=`cat $1 $2 | wc | awk '{ print $1 }'`
union=`cat $1 $2 | sort -u | wc | awk '{ print $1 }'`
intersection=`echo $total $union | awk '{ print $1-$2 }'`
jaccard=`echo $intersection $union | awk '{ print $1 / $2 }'`
echo "Total: $total"
echo "Union: $union"
echo "Intersection: $intersection"
echo "Jaccard: $jaccard"
|
It's not too slow on the professorial words files (this is on my 2.2 GHz Macbook Pro):
UNIX> time sh minhash.sh Words/01-Plank.txt Words/02-Abidi.txt Total: 552 Union: 511 Intersection: 41 Jaccard: 0.0802348 0.014u 0.015s 0:00.02 100.0% 0+0k 0+0io 0pf+0w UNIX>But it's pretty brutal on the larger files:
UNIX> time sh minhash.sh Names/01.txt Names/02.txt Total: 2000000 Union: 1100000 Intersection: 900000 Jaccard: 0.818182 43.121u 0.227s 0:43.27 100.1% 0+0k 0+9io 0pf+0w UNIX>On the flip side, this gives us a way to verify that our other implementations are correct. Let's go ahead and make two files:
UNIX> time sh make-verify.sh Words/* Miller.txt Yaakobi.txt Tarjan.txt > Words-Verify.txt 27.107u 30.734s 0:35.39 163.4% 0+0k 0+4io 0pf+0w UNIX> time sh make-verify.sh Names/* > Names-Verify.txt 391.009u 1.973s 6:32.34 100.1% 0+0k 0+112io 0pf+0w UNIX>We can see the five professors who are most similar to me:
UNIX> grep '^Words.01' Words-Verify.txt | sort -nr -k 3 | head -n 5 Words/01-Plank.txt Words/01-Plank.txt 1.000000 Words/01-Plank.txt Words/03-Beck.txt 0.267717 Words/01-Plank.txt Miller.txt 0.160633 Words/01-Plank.txt Words/16-Huang.txt 0.138614 Words/01-Plank.txt Words/06-Cao.txt 0.129754 UNIX>That does not surprise me at all (I've written quite a few papers with Dr. Beck).
UNIX> g++ -o calc-error calc-error.cpp UNIX> calc-error Words-Verify.txt Words-Verify.txt 0.00000000 UNIX> calc-error Names-Verify.txt Names-Verify.txt 0.00000000 UNIX>
UNIX> time control Names/* 0.411u 0.012s 0:00.42 100.0% 0+0k 0+0io 0pf+0w UNIX>
for (i = 0; i < sets.size(); i++) {
for (j = 0; j < sets.size(); j++) {
Total = sets[i].size() + sets[j].size();
Intersection = 0;
for (lit = sets[j].begin(); lit != sets[j].end(); lit++) {
if (sets[i].find(*lit) != sets[i].end()) Intersection++;
}
Union = Total - Intersection;
printf("%-30s %-30s %.6lf\n", argv[i+1], argv[j+1], Intersection / Union);
}
}
}
|
I compile it with -O3, and while it is smoking fast on the small data set, it's pretty slow on the large one. You'll see that I verify it against the shell script, and I get zero error, as anticipated.
UNIX> time jaccard-set-lazy Words/* Miller.txt Yaakobi.txt Tarjan.txt > tmp.txt 0.062u 0.001s 0:00.06 100.0% 0+0k 0+3io 0pf+0w UNIX> calc-error Words-Verify.txt tmp.txt 0.000000 UNIX> time jaccard-set-lazy Names/* > tmp.txt 7.696u 0.120s 0:07.82 99.8% 0+0k 0+3io 0pf+0w UNIX> calc-error Names-Verify.txt tmp.txt 0.000000 UNIX>
for (i = 0; i < sets.size(); i++) {
for (j = 0; j < sets.size(); j++) {
Total = sets[i].size() + sets[j].size();
Intersection = 0;
liti = sets[i].begin();
litj = sets[j].begin();
while (liti != sets[i].end() && litj != sets[j].end()) {
if (*liti == *litj) {
Intersection++;
liti++;
litj++;
} else if (*liti < *litj) {
liti++;
} else {
litj++;
}
}
Union = Total - Intersection;
printf("%-30s %-30s %.6lf\n", argv[i+1], argv[j+1], Intersection / Union);
}
}
|
This speeds us up a little:
UNIX> time jaccard-set-linear Names/* > tmp.txt 5.436u 0.116s 0:05.56 99.6% 0+0k 0+0io 0pf+0w UNIX> calc-error Names-Verify.txt tmp.txt 0.000000 UNIX>Instead of using a set, we can read the lines into vectors and sort them. While that has the same big-O complexity as the set implementation, it should be more time and space efficient. The code is in jaccard-sort.cpp, and it's really straightforward:
/* Sort the vectors. */
for (i = 0; i < sets.size(); i++) sort(sets[i].begin(), sets[i].end());
/* For each pair of sets, calculate the Jaccard similarity directly. */
for (i = 0; i < sets.size(); i++) {
for (j = 0; j < sets.size(); j++) {
Total = sets[i].size() + sets[j].size();
Intersection = 0;
ip = 0;
jp = 0;
while (ip < sets[i].size() && jp < sets[j].size()) {
if (sets[i][ip] == sets[j][jp]) {
Intersection++;
ip++;
jp++;
} else if (sets[i][ip] < sets[j][jp]) {
ip++;
} else {
jp++;
}
}
Union = Total - Intersection;
printf("%-30s %-30s %.6lf\n", argv[i+1], argv[j+1], Intersection / Union);
}
}
}
|
It also is more than twice as fast:
UNIX> time jaccard-sort Names/* > tmp.txt 1.782u 0.054s 0:01.84 99.4% 0+0k 0+3io 0pf+0w UNIX> calc-error Names-Verify.txt tmp.txt 0.000000 UNIX>
while (getline(f, s)) {
MD5((const unsigned char *) s.c_str(), s.size(), md5_buf);
memcpy(&ull, md5_buf, sizeof(unsigned long long));
sets[i-1].push_back(ull);
}
f.close();
}
|
The rest of the code is identical. That shaves 21% off the running time:
UNIX> time jaccard-sort-hash Names/* > tmp.txt 1.408u 0.025s 0:01.43 99.3% 0+0k 0+0io 0pf+0w UNIX> calc-error Names-Verify.txt tmp.txt 0.000000 UNIX>
What we're going to do is figure out how many bytes of hashes we need, and allocate room, padded to a multiple of 16. Then, for each chunk of 16 bytes, we are going to calculate an MD5 hash, where we XOR a number from 0 to 216-1 with the first two bytes of the string. After calculating each hash, we'll XOR with the number again, which will turn the two bytes back to their original values. This will generate up to 220 bytes of hashes, which should be enough. We are going to make sure that our strings have at least two characters, so that this works.
For each data set, we'll maintain a similar region of hashes, and we'll use memcmp() to makes sure that we maintain the minimum hash for each of the k hashes. We're going to have the number of bytes in each hash be a variable on the command line. That way, we can use two-byte hashes when the number of elements of the set is small, and three or four-byte hashes when it's bigger.
Let's look at some code, and print some state. My code is in min-hash-k.cpp. Here are the important variable declarations:
int main(int argc, char **argv)
{
vector <string> files; // Filenames
vector <unsigned char *> min_hashes; // The minimum hashes for each file.
int k; // The number of hashes
int bbh; // Bytes per hash
int hash_buf_size; // Size of the hash buffers (k*bbh) padded to 16
unsigned int ff; // An integer that holds 0xffffffff
unsigned char *hash; // Where we calculate the hashes for each string.
|
First, we calculate how big the hash buffers should be, and then we allocate a buffer for hash and a vector of hash buffers for each file. We initialize the file buffers to all f's, and print them out:
/* Calculate the number of bytes for all of the hashes, and allocate a
hash buffer for temporary use, and a hash buffer for each data set
to hold the minimum hashes for each data set. Set each byte of
these buffers to 0xff, which is their maximum value, regardless of the
size of the hash. */
hash_buf_size = k * bbh;
if (hash_buf_size % 16 != 0) hash_buf_size += (16 - hash_buf_size % 16);
ff = 0xffffffff;
hash = (unsigned char *) malloc(hash_buf_size);
min_hashes.resize(files.size());
for (i = 0; i < min_hashes.size(); i++) {
min_hashes[i] = (unsigned char *) malloc(hash_buf_size);
for (j = 0; j < hash_buf_size; j += sizeof(int)) {
memcpy(min_hashes[i]+j, &ff, sizeof(int));
}
}
/* Error check code #1: Print out the initial values of all the hashes,
which should all be ff's */
for (i = 0; i < min_hashes.size(); i++) {
printf("%20s ", files[i].c_str());
for (j = 0; j < k * bbh; j++) printf("%02x", min_hashes[i][j]);
printf("\n");
}
|
Let's test this on the three files in Names, using 6 for k ahd 3 for bbh. We need 18 bytes for the hash regions, which, when padded to 16 is 32 bytes:
UNIX> min-hash-k 6 3 Names/*.txt
Names/01.txt ffffffffffffffffffffffffffffffffffff
Names/02.txt ffffffffffffffffffffffffffffffffffff
Names/03.txt ffffffffffffffffffffffffffffffffffff
UNIX> echo ffffffffffffffffffffffffffffffffffff | wc
1 1 37
UNIX>
That last command verifies that we have 18 bytes in the hash buf -- each byte is two
hex digits, and the echo command adds a newline, so 37 characters is the correct
number of characters.
Next, here is the code that reads in each string, calculates the hashes, and then compares the k hashes to the min_hashes, setting min_hashes when the hashes are smaller. This also has the code that xor's the first two bytes of the string, so that you can generate up to 216 different MD5 hashes:
/* Read the data sets. For each value, you're going to calculate the k hashes
and then update the minimum hashes for the data set. */
for (findex = 0; findex < files.size(); findex++) {
f.clear();
f.open(files[findex].c_str());
if (f.fail()) { perror(files[findex].c_str()); exit(1); }
while (getline(f, s)) {
if (s.size() < 2) {
fprintf(stderr, "File %s - can't have one-character strings.\n", files[findex].c_str());
exit(1);
}
/* Here is where we calculate the hash_buf_size bytes of hashes. */
j = 0;
sz = s.size();
for (i = 0; i < hash_buf_size; i += 16) {
s[0] ^= (j & 0xff);
s[1] ^= (j >> 8);
MD5((unsigned char *) s.c_str(), sz, hash+i);
s[0] ^= (j & 0xff);
s[1] ^= (j >> 8);
j++;
}
/* And here is where we compare each unit of bbh bytes with the unit in min_hashes,
and if it's smaller, we set the bbh bytes of min_hashes to the bytes in hash: */
j = 0;
for (i = 0; i < k * bbh; i += bbh) {
if (memcmp(hash+i, min_hashes[findex]+i, bbh) < 0) {
memcpy(min_hashes[findex]+i, hash+i, bbh);
}
}
/* Error check code #2: Print the hashes and the min hashes. */
printf("%-20s %-20s\n", files[findex].c_str(), s.c_str());
printf(" hash: ");
for (i = 0; i < k*bbh; i++) printf("%s%02x", (i%bbh == 0) ? " " : "", hash[i]);
printf("\n minh: ");
for (i = 0; i < k*bbh; i++) printf("%s%02x", (i%bbh == 0) ? " " : "", min_hashes[findex][i]);
printf("\n");
}
f.close();
}
|
Let's test -- I'm going to create a small file with three words, and then take a look at the output when k is 3 and bbh is 2:
UNIX> ( echo Give ; echo Him ; echo Six ) > junk.txt UNIX> cat junk.txt Give Him Six UNIX> min-hash-k 3 2 junk.txt junk.txt Give hash: 2f35 5d9f a7ac minh: 2f35 5d9f a7ac junk.txt Him hash: b582 f0dd d1c3 minh: 2f35 5d9f a7ac junk.txt Six hash: e6fb c0b9 673f minh: 2f35 5d9f 673f UNIX>As you can see, with the string "Give", all three hashes were set to the hashes of "Give". that's because they were all initialized to 0xffff. With "Him", the three hashes were all bigger than the hashes for "Give", so min_hash was unchanged. With "Six", the last hash, 0x673f, was smaller than 0xa7ac, so the third hash of min_hash was changed.
Let's do a second test where we have to calculate a second hash, just to make sure that it's different from the first:
UNIX> min-hash-k 2 16 junk.txt junk.txt Give hash: 2f355d9fa7accc561d3edc335de2fbcf e5d9de39f7ca1ba2637e5640af3ae8aa minh: 2f355d9fa7accc561d3edc335de2fbcf e5d9de39f7ca1ba2637e5640af3ae8aa junk.txt Him hash: b582f0ddd1c3852810de9cb577293351 07ec74942cd2e4040c9c6c62cfdfaa4f minh: 2f355d9fa7accc561d3edc335de2fbcf 07ec74942cd2e4040c9c6c62cfdfaa4f junk.txt Six hash: e6fbc0b9673f8c86726688d7607fc8f5 bd717113c3cafa1681fe96b05c8b3645 minh: 2f355d9fa7accc561d3edc335de2fbcf 07ec74942cd2e4040c9c6c62cfdfaa4f UNIX>And, let's do a final test where we generate over 256 hashes, to make sure that our XOR code is working on the second byte as well. To do that, we'll use k equal to 258 and bbh equal to 16 again. We'll grep for "hash" to isolate the lines that have the hash values, and then we'll put those lines into a temporary file:
UNIX> min-hash-k 258 16 junk.txt | grep hash > tmp.txtNext, let's use awk to print out all of the hash values, one per line:
UNIX> awk '{ for (i=2; i <= NF; i++) print $i }' < tmp.txt | head
2f355d9fa7accc561d3edc335de2fbcf
e5d9de39f7ca1ba2637e5640af3ae8aa
ee759d6725400149983a4b7ba847130f
096f6d7168640882498c00b9142932e7
3501ace2a69bb89b3981554306a60a57
a5ebcbceb6e1ec0356db8e4b7faf5d94
e37b483220e5802754d870863327567d
b7f4c393b08b1866b8409e3f169fdc89
7a3c17bf9a2d9b42123cc229ecb04bce
4276d507cb57cf5eedac31e10cbe3f54
UNIX>
Finally, let's count the unique hash values with sort -u. The answer should
be 258*3 = 774.
UNIX> awk '{ for (i=2; i <= NF; i++) print $i }' < tmp.txt | sort -u | wc
774 774 25542
UNIX>
Ok -- I'm happy. Now that we have min_hashes set for every data file, we simply
compare them. Here's the code for that. Do you see how nice memcmp() and memcpy()
have been to use?
/* Error check #3: Let's print out the min hashes, so that we can double-check. */
for (findex = 0; findex < files.size(); findex++) {
printf("%-10s ", files[findex].c_str());
for (i = 0; i < k*bbh; i++) printf("%s%02x", (i%bbh == 0) ? " " : "", min_hashes[findex][i]);
printf("\n");
}
/* For each pair of files, compare the hashes. */
for (i = 0; i < files.size(); i++) {
for (j = 0; j < files.size(); j++) {
Intersection = 0;
for (l = 0; l < k*bbh; l += bbh) {
if (memcmp(min_hashes[i]+l, min_hashes[j]+l, bbh) == 0) Intersection++;
}
printf("%-30s %-30s %.6lf\n", files[i].c_str(), files[j].c_str(), Intersection / (double) k);
}
}
exit(0);
}
|
As always, there's a temptation to simply let this code rip on our bigger data sets, but let's do a small test first, to make sure that everything makes sense. Here, I'm going to make three files with three words each. The first two share two words, and the second two share one word. The first and third share zero words:
UNIX> rm -f junk*.txt UNIX> ( echo Give ; echo Him ; echo Six ) > junk1.txt UNIX> ( echo Give ; echo Him ; echo Ten ) > junk2.txt UNIX> ( echo Eight ; echo Nine ; echo Ten ) > junk3.txt UNIX> min-hash-k 5 4 junk1.txt junk2.txt junk3.txt junk1.txt 2f355d9f 673f8c86 10de9cb5 5de2fbcf 07ec7494 junk2.txt 2f355d9f 38dca5ef 10de9cb5 5de2fbcf 07ec7494 junk3.txt 24db1121 38dca5ef 172c33cf 3def2f3f 08cd928e junk1.txt junk1.txt 1.000000 junk1.txt junk2.txt 0.800000 junk1.txt junk3.txt 0.000000 junk2.txt junk1.txt 0.800000 junk2.txt junk2.txt 1.000000 junk2.txt junk3.txt 0.200000 junk3.txt junk1.txt 0.000000 junk3.txt junk2.txt 0.200000 junk3.txt junk3.txt 1.000000 UNIX>You can verify easily by looking at the hashes, that junk1.txt and junk2.txt share hashes 0, 2, 3 and 4. junk2.txt and junk3.txt share hash 1. And junk1.txt and junk3.txt share nothing. The output looks good! We'll comment out our error checking code, and do a little testing on our two data sets. Let's start with the Names data set, because it's easier to look at the output.
UNIX> time min-hash-k 10 4 Names/*.txt Names/01.txt 00002300 000021a5 000000bd 000002f9 000008a4 00001488 000017f6 000008c9 00000dc5 00000dc4 Names/02.txt 00002300 00000126 000000bd 000002f9 000008a4 00001488 000017f6 00000628 00000dc5 00000dc4 Names/03.txt 00002300 00000126 000000bd 000002f9 000008a4 00001488 000017f6 00000628 00000dc5 00000dc4 Names/01.txt Names/01.txt 1.000000 Names/01.txt Names/02.txt 0.800000 Names/01.txt Names/03.txt 0.800000 Names/02.txt Names/01.txt 0.800000 Names/02.txt Names/02.txt 1.000000 Names/02.txt Names/03.txt 1.000000 Names/03.txt Names/01.txt 0.800000 Names/03.txt Names/02.txt 1.000000 Names/03.txt Names/03.txt 1.000000 2.837u 0.021s 0:02.86 99.6% 0+0k 2+0io 0pf+0w UNIX>I forgot to comment out the error checking code, but that's ok, because it's a good sanity check. Does that look buggy to you? It scared me at first, because every hash started with 0000. However, think about it -- you have 1,000,000 words. What are the chances that one will start with 0000? The answer to that is 1 - (65535/65536)1,000,000. You can calculate that one by hand:
UNIX> echo "" | awk '{ l=1.0; for (i = 0; i < 1000000; i++) { l *= (65535/65536); print l}}' | head
0.999985
0.999969
0.999954
0.999939
0.999924
0.999908
0.999893
0.999878
0.999863
0.999847
UNIX> echo "" | awk '{ l=1.0; for (i = 0; i < 1000000; i++) { l *= (65535/65536); print l}}' | tail
2.36157e-07
2.36154e-07
2.3615e-07
2.36146e-07
2.36143e-07
2.36139e-07
2.36136e-07
2.36132e-07
2.36128e-07
2.36125e-07
UNIX>
Yes, the chances are really high that all of the numbers start with 0000. Ok, back to
the test:
UNIX> cat Names-Verify.txt Names/01.txt Names/01.txt 1.000000 Names/01.txt Names/02.txt 0.818182 Names/01.txt Names/03.txt 0.666667 Names/02.txt Names/01.txt 0.818182 Names/02.txt Names/02.txt 1.000000 Names/02.txt Names/03.txt 0.818182 Names/03.txt Names/01.txt 0.666667 Names/03.txt Names/02.txt 0.818182 Names/03.txt Names/03.txt 1.000000 UNIX> time min-hash-k 10 4 Names/*.txt > junk.txt 2.933u 0.015s 0:02.95 99.6% 0+0k 0+2io 0pf+0w UNIX> cat junk.txt Names/01.txt Names/01.txt 1.000000 Names/01.txt Names/02.txt 0.800000 Names/01.txt Names/03.txt 0.800000 Names/02.txt Names/01.txt 0.800000 Names/02.txt Names/02.txt 1.000000 Names/02.txt Names/03.txt 1.000000 Names/03.txt Names/01.txt 0.800000 Names/03.txt Names/02.txt 1.000000 Names/03.txt Names/03.txt 1.000000 UNIX> calc-error Names-Verify.txt junk.txt 0.074074 UNIX> time min-hash-k 100 4 Names/*.txt > junk.txt 20.184u 0.017s 0:20.20 99.9% 0+0k 0+4io 0pf+0w UNIX> cat junk.txt Names/01.txt Names/01.txt 1.000000 Names/01.txt Names/02.txt 0.870000 Names/01.txt Names/03.txt 0.710000 Names/02.txt Names/01.txt 0.870000 Names/02.txt Names/02.txt 1.000000 Names/02.txt Names/03.txt 0.820000 Names/03.txt Names/01.txt 0.710000 Names/03.txt Names/02.txt 0.820000 Names/03.txt Names/03.txt 1.000000 UNIX> calc-error Names-Verify.txt junk.txt 0.021549 UNIX> time min-hash-k 1000 4 Names/*.txt > junk.txt 197.086u 0.038s 3:17.12 99.9% 0+0k 0+2io 0pf+0w UNIX> calc-error Names-Verify.txt junk.txt 0.011326 UNIX>Well, my conclusion from this is that this version of min-hash, much like bubble-sort, is almost irresponsible to teach. It makes sense -- for this data set, log(n) is 20, so setting k to 1000 is going to be a clear loser time-wise. And all for an accuracy lower than 99 percent? This is terrible. As you'll see below, the one-hash version of min-hash is very nice, so this version, with all of its yucky coding, is destined for the trash heap. So it goes.
for (findex = 0; findex < files.size(); findex++) {
f.clear();
f.open(files[findex].c_str());
if (f.fail()) { perror(files[findex].c_str()); exit(1); }
while (getline(f, s)) {
MD5((unsigned char *) s.c_str(), s.size(), hash);
memcpy((unsigned char *) &ll, hash, sizeof(long long));
/* Error check code 1: Print out the hashes. */
printf("%-20s 0x%016llx\n", s.c_str(), ll);
if (min_hashes[findex].size() < k) {
min_hashes[findex].insert(ll);
} else {
liti = min_hashes[findex].begin();
if (ll > *liti) {
min_hashes[findex].insert(ll);
if (min_hashes[findex].size() > k) min_hashes[findex].erase(liti);
}
}
}
}
/* Error check code #2: Print out the min hashes. */
for (findex = 0; findex != files.size(); findex++) {
printf("%s\n", files[findex].c_str());
for (liti = min_hashes[findex].begin(); liti != min_hashes[findex].end(); liti++) {
printf(" 0x%016llx\n", *liti);
}
}
|
Here's my error checking code. First, I set k to ten, so that it keeps all of the hashes:
UNIX> ( echo Give ; echo Him ; echo Six ; echo Touchdown ; echo Tennessee ) > junk1.txt UNIX> min-hash-1 10 junk1.txt Give 0x56ccaca79f5d352f Him 0x2885c3d1ddf082b5 Six 0x868c3f67b9c0fbe6 Touchdown 0x8a3287e254ab0f3b Tennessee 0x5265f51b083bc5a5 junk1.txt 0x2885c3d1ddf082b5 0x5265f51b083bc5a5 0x56ccaca79f5d352f 0x868c3f67b9c0fbe6 0x8a3287e254ab0f3b UNIX>And next I set k to two, and keep the two largest hashes:
UNIX> min-hash-1 2 junk1.txt Give 0x56ccaca79f5d352f Him 0x2885c3d1ddf082b5 Six 0x868c3f67b9c0fbe6 Touchdown 0x8a3287e254ab0f3b Tennessee 0x5265f51b083bc5a5 junk1.txt 0x868c3f67b9c0fbe6 0x8a3287e254ab0f3b UNIX>Now, I'll calculate the Jaccard similarity of the set, just like I did above in jaccard-set-linear.cpp. First, test for correctness:
UNIX> min-hash-1 10000000 Names/* > junk.txt UNIX> calc-error Names-Verify.txt junk.txt 0.000000 UNIX>And let's time it and check accuracy.
UNIX> time min-hash-1 10 Names/* > junk.txt 1.162u 0.011s 0:01.17 100.0% 0+0k 0+1io 0pf+0w UNIX> calc-error Names-Verify.txt junk.txt 0.062160 UNIX> time min-hash-1 100 Names/* > junk.txt 1.231u 0.012s 0:01.24 100.0% 0+0k 0+0io 0pf+0w UNIX> calc-error Names-Verify.txt junk.txt 0.054892 UNIX> time min-hash-1 1000 Names/* > junk.txt 1.242u 0.013s 0:01.25 100.0% 0+0k 0+1io 0pf+0w UNIX> calc-error Names-Verify.txt junk.txt 0.006717 UNIX> time min-hash-1 10000 Names/* > junk.txt 1.218u 0.013s 0:01.23 99.1% 0+0k 0+3io 0pf+0w UNIX> calc-error Names-Verify.txt junk.txt 0.003341 UNIX>