 |
people = [[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]] answer = [[5,0], [7,0], [5,2], [6,1], [4,4], [7.1]]This is the only order where the (hi,ni) make sense.
people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]] answer = [[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]Again, this is the only order where the (hi,ni) make sense.
I mused a bit, and thought about doing the O(n log n) implementation, but it seemed bug-prone, and the success rate was 72%. Surely 72% of the programmers weren't implementing their own O(n log n) data structure.
So I wrote up the O(n2) solution, and not only was it fast enough, but it was faster than 86% of the programmers. What? Usually my solutions are faster than 5%, and I think they're pretty efficient.
At that point, I couldn't help myself -- I implemented the O(n log n) solution, and indeed it was bug prone, but since I knew it would be, I was able to iron out the kinks before moving it to leetcode. And then -- faster than 96% of the solutions! How rewarding!
As it turns out, as O(n2) solutions go, mine was fast. When I did the problem again in May, 2023, with only my sketchy notes to help me, I came up with a much slower O(n2) solution -- faster than 13% and smaller than 35%.
So let's go over them. You should write up Solution 2 below, or if you're feeling really ambitious, Solution 3.
people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]] answer = [[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]Our O(n2) solution is straightforward: Consider the shortest person. In Example 2, that's the person of height 1, where 4 people of height ≥ 4 are in front of the person. That person must be in array index 4. So let's put it there -- here's our return value. We know the vector must have 6 entries -- so we'll create it. However, we'll only resize rv[i] when we set its answer.
Here's the return value after inserting [1,4]:
Value: ----- ----- ----- ----- [1,4] ----- Index: 0 1 2 3 4 5 |
We continue iteratvely -- find the person with the next smallest height: [2,2]. That person has to go into index 2:
Value: ----- ----- [2,2] ----- [1,4] ----- Index: 0 1 2 3 4 5 |
The next person is [3,2]. Well, index 2 is taken, but since person 3 has a greater height than person 2, we can ignore person two. Essentially, we renumber the vector to not include "taken" values:
Value: ----- ----- [2,2] ----- [1,4] ----- Index: 0 1 2 3 |
So now we can insert [3,2] into entry 2:
Value: ----- ----- [2,2] [3,2] [1,4] ----- Index: 0 1 2 |
And so on, until you get the answer:
Value: [4,0] [5,0] [2,2] [3,2] [1,4] [6,0] |
When I finished with a person, I set his/her height to 1,000,001, which made looking for the "next" person easier.
So that solves the case when all people have different heights. What about people with the same height? If you think about it, when you look for people with the smallest height, you can simply break ties in favor of those whose ni values are greater. Consider the first example:
people = [[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]] answer = [[5,0], [7,0], [5,2], [6,1], [4,4], [7.1]] |
We'll start by placing [4,4]:
----- ----- ----- ----- [4,4] ----- 0 1 2 3 4 |
Now, we see two people with heights of 5. We break ties in favor of higher ni, so we place [5,2]:
----- ----- [5,2] ----- [4,4] ----- 0 1 2 3 |
And then [5,0]:
[5,0] ----- [5,2] ----- [4,4] -----
0 1 2
|
And so on.
map <int, set <int> > M; |
I ran through the array and inserted people into the map. The key was the hi value and then I inserted the ni into the set. This allows me to handle people with the same height all in one pass.
Consider the first example. Here's my map:
4: { 4 }
5: { 0, 2 }
6: { 1 }
7: { 0, 1 }
|
Instead of taking 6 passes through the vector, I'm only taking four:
Pass 1: ----- ----- ----- ----- [4,4] -----
0 1 2 3 4
|
Only taking 4 passes is helpful to the running time, but, even more importantly, after creating the map, I take O(1) to find the smallest height, rather than O(n). That's why this one was fast.
Implementing this in O(n2) time is straightforward. Each time you want to put something into the return value, you can figure out the proper entry by starting from the beginning of the return value, and counting the empty entries until you get to the place where each value should go. Since you are potentially traversing the entire array each time, it is O(n2).
You can go ahead and implement this, but read the final implementation.
void initialize(int n); // Create a return vector with n empty slots. int find(int i); // Return the index of the ith empty slot void fill(int i); // Index i is empty. Set it as non-empty.When all of the entries are "filled", you can get the final return value.
So, with example 1, we would do the following:
- Initialize(6) - considering [4,4]: find(4) = 4. Put [4,4] into rv[4]. Then call fill(4). - considering [5,2]: find(2) = 2. Put [5,2] into rv[2]. Then call fill(2). - considering [5,0]: find(0) = 0. Put [5,0] into rv[0]. Then call fill(0). - considering [6,1]: find(1) = 3. Put [6,1] into rv[3]. Then call fill(3). - considering [7,1]: find(1) = 5. Put [7,1] into rv[5]. Then call fill(5). - considering [7,0]: find(0) = 1. Put [7,0] into rv[1]. Then call fill(1).At this point, you're done and:
rv = [ [5,0] [7,0] [5,2] [6,1] [4,4] [7,1] ] |
So, if you can implement find() and fill() in log(n) time, then your solution will be O(n log n).
The problem is that I don't see a way to implement find() and fill() with STL data structures. So I rolled my own. I defined a binary tree with the following fields:
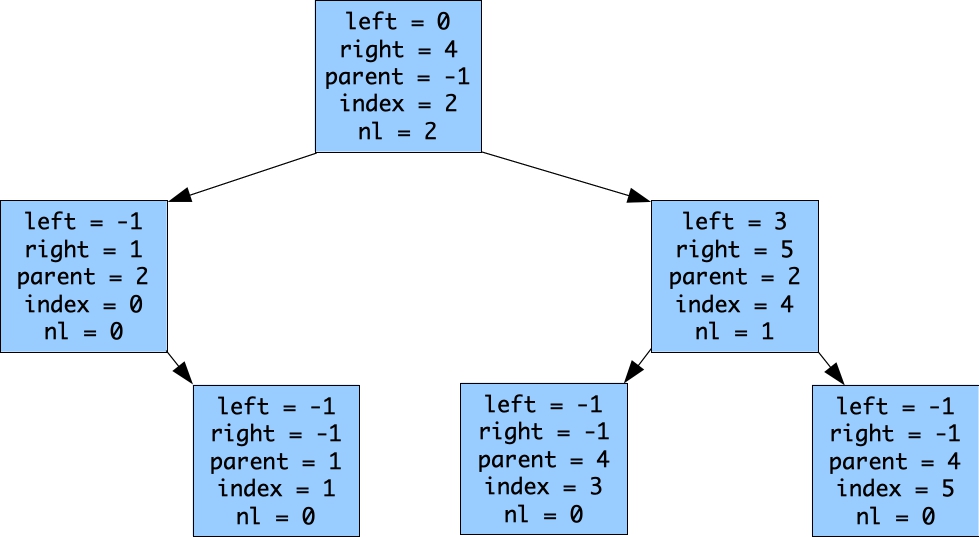
- left = root of left subtree - right = root of right subtree - parent = parent of the node - index = index of the return value if unused. -1 otherwise. - nl = number of unused indices in the left subtreeWith this tree structure, you can implement find() and fill() in log time. Let's use example 1 to illustrate. When I initialize, here's my tree:
 |
The first thing I do is find(4), which returns 4. How do you do that? Use the nl fields and chase tree pointers. After we fill in entry 4 of the return value, we call fill(4), which says that entry 4 is no longer empty. When you're done, here's the tree:
 |
I've drawn the node in yellow to show that it's no longer empty. Nothing else has changed. Now, we call find(2), which will return 2. We then call fill(2), and when that's done, here's the state:
 |
We now call find(0). That will return 0, and we then call fill(0). When that's done, here's the data structure:
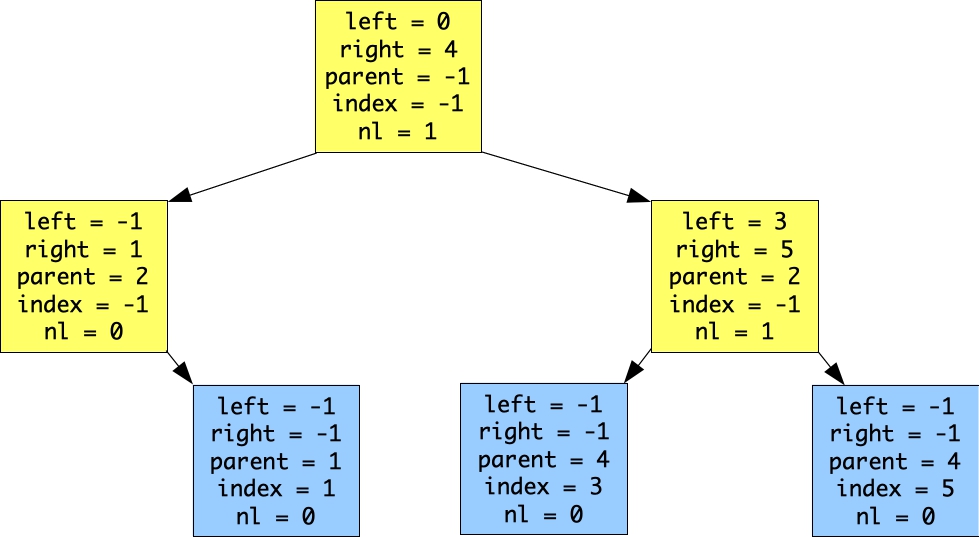 |
Note how nl in the root node has changed - that's part of the job of fill() -- to travel up to the root, updating nl if necessary.
The next call is find(1), which returns the node whose index is 3. When we call fill(3), our tree becomes:
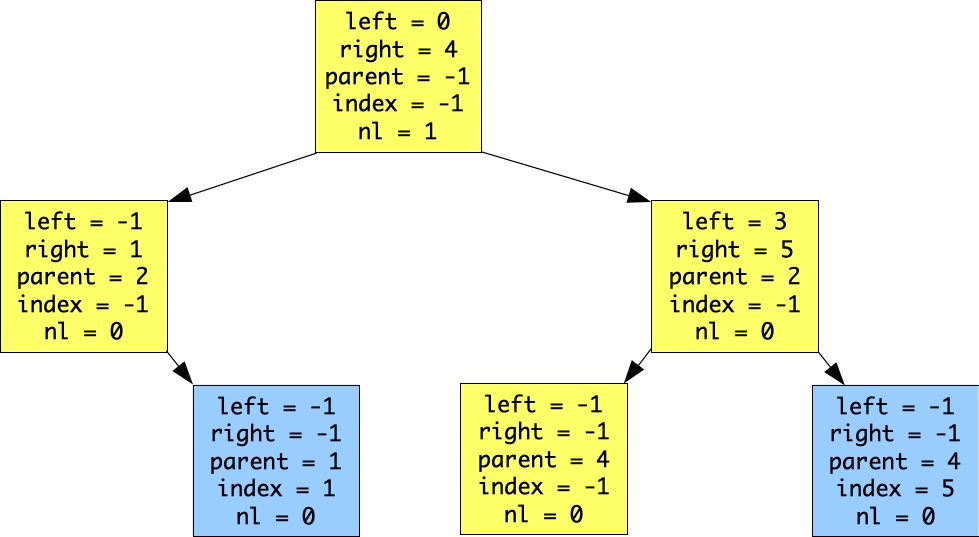 |
Ok -- hopefully that gives you enough help to finish the O(n log n) solution. As I said above, it was faster than 96% of the other correct submissions.