Dining Philosophers

The book (again, chapter 6) has an excellent description of dining philosophers. I'll be a little more sketchy.

The problem is defined as follows: There are 5 philosophers sitting at a round table. Between each adjacent pair of philosophers is a chopstick. In other words, there are five chopsticks. Each philosopher does two things: think and eat. The philosopher thinks for a while, and then stops thinking and becomes hungry. When the philosopher becomes hungry, he/she cannot eat until he/she owns the chopsticks to his/her left and right. When the philosopher is done eating he/she puts down the chopsticks and begins thinking again.

Of course, the definition of this problem always leads me to ask a few questions:

1. If these philosophers are so smart, shouldn't they be worried about communicable diseases?
2. Why chopsticks? For some reason I envision philosophers liking soup.
3. Evidently conversing isn't in here -- why do they need to be at the same table? I'm not sure if I'd enjoy having a philosopher philosophize while I'm eating. But then again, I'm not a philosopher.
4. Shouldn't bathing be in the equation somewhere?

The challenge in the dining philosophers problem is to design a protocol so that the philosophers do not deadlock (i.e. every philosopher has a chopstick), and so that no philosopher starves (i.e. when a philosopher is hungry, he/she eventually gets the chopsticks). Additionally, our protocol should try to be as efficient as possible -- in other words, we should try to minimize the time that philosophers spent waiting to eat.

(In case you're bored, here is that last paragraph in the inimitable words of professor Wolski: ``Since these are either unwashed, stubborn and deeply committed philosophers or unwashed, clueless, and basically helpless philosophers, there is a possibility for deadlock. In particular, if all philosophers simultaneously grab the chopstick on their left and then reach for the chopstick on their right (waiting until one is available) before eating, they will all starve. The challenge in the dining philosophers problem is to design a protocol so that the philosophers do not deadlock (i.e. the entire set of philosophers does not stop and wait indefinitely), and so that no philosopher starves (i.e. every philosopher eventually gets his/her hands on a pair of chopsticks).'')

Dining Philosophers Testbed with pthreads

The driver is in dphil_skeleton.c (here's dphil.h too). It works as follows. First it calls initialize_v(), which is a procedure that is undefined. It expects a (void *) in return. This pointer will be passed to all procedures as part of the Phil_struct struct, and the user should initialize it however he/she likes.

Next, the driver does a few other things, and finally forks off the philosopher threads (the total number of philosophers is a command line argument). After doing so, the main thread sleeps for ten seconds, and prints out information about how long each philosopher has been blocked, waiting to eat. This is so that you can make some assessment of how good the protocols are at letting philosophers eat.

Now, the philosophers basically go through the following steps.

while(1) {
  think for a random number of seconds
  pickup(p);
  eat for a random number of seconds
  putdown(p);
}

Each solution to this problem must implement initialize_v(), pickup() and putdown() to manage the chopsticks. Pickup() and putdown() should be written so that no philosopher starves (i.e. wants to eat, but never gets a chopstick), and so that deadlock doesn't occur (a subset of the above, because it would mean that all philosophers starve...) It should also attempt to try to minimize the amount of time that the philosopher's spend waiting for chopsticks.

Solutions to the dining philosophers

Here are descriptions of the solution programs:

Solution #1 -- No solution

UNIX> dphil_1 5 10
  0 Total blocktime:     0 :     0     0     0     0     0
  0 Philosopher 0 thinking for 2 seconds
  0 Philosopher 1 thinking for 7 seconds
  0 Philosopher 2 thinking for 3 seconds
  0 Philosopher 3 thinking for 5 seconds
  0 Philosopher 4 thinking for 8 seconds
  3 Philosopher 0 no longer thinking -- calling pickup()
  4 Philosopher 0 eating for 5 seconds
  5 Philosopher 2 no longer thinking -- calling pickup()
  5 Philosopher 2 eating for 10 seconds
  9 Philosopher 3 no longer thinking -- calling pickup()
  9 Philosopher 3 eating for 7 seconds

I include this as a solution because it shows how you link everything up with dphil_skeleton.c. In lab 2, the problems both have skeletons like dphil_skeleton.c and null solutions like dphil_1.c, just to show you how to link things together.

Solution #2 -- A mutex for each chopstick

This is prone to deadlock, although on this system you really won't ever see it because of the granularity of timeslicing between threads. The only time that this solution is a problem is if a philosopher's thread gets preempted between picking up the first and the second mutex. That doesn't really ever happen here, so it looks like it works just fine.

dp_2_out.txt, you'll see the output of running dphil_2 5 10 for 2100 seconds. There's no deadlock, but as you'll see later, the threads spend more time blocked than they should. I'll let you think about why. Here is the last line of the file:

Solution #3 -- Showing how you get deadlock with solution #2

UNIX> dphil_3 5 3
  0 Total blocktime:     0 :     0     0     0     0     0 
  0 Philosopher 0 thinking for 3 seconds
  0 Philosopher 1 thinking for 1 second
  0 Philosopher 2 thinking for 1 second
  0 Philosopher 3 thinking for 1 second
  0 Philosopher 4 thinking for 2 seconds
  1 Philosopher 3 no longer thinking -- calling pickup()
  1 Philosopher 2 no longer thinking -- calling pickup()
  1 Philosopher 1 no longer thinking -- calling pickup()
  2 Philosopher 4 no longer thinking -- calling pickup()
  3 Philosopher 0 no longer thinking -- calling pickup()
 10 Total blocktime:    42 :     7     9     9     9     8 
 20 Total blocktime:    92 :    17    19    19    19    18 
  ...

Solution #4 -- An asymmetrical solution

There are two problems with this solution. The first is minor. This solution can exhibit starvation depending on how the thread system is implemented. For example, suppose philosopher A is waiting for a chopstick. Eventually, the owner of the chopstick (philosopher B) will eat and put the chopstick down, but there's no guarantee that philosopher A will get it if philosopher B wants to eat again before philosopher A's thread is rescheduled. Given our thread system and the randomness in the sleep() calls, that does not appear to be a problem, but it could well be on a different system with different parameters.

The more major problem is that the philosophers are not equally weighted here. If you look at dp_4_out.txt, you'll see the output of running dphil_4 5 10 for 2100 seconds. The interesting thing here is the block-times. You'll note that philosopher #4 blocks for much less time than the rest. Why? The reason is kind of subtle. Suppose all the philosophers want to eat at the same time. Philosophers 0 and 1 will have to fight for their first chopstick, as will philosophers 2 and 3. However, philosopher 4 will always get his first chopstick. This phenomenon (which is really more complex than that, but that's the basis of it) gives philosopher 4 an advantage over the others, meaning he eats more. Thus, if you are looking to give all the philosophers equal weight, you can't use this solution.

Solution #5 -- The book's solution

The basic premise behind the solution is this: When a philosopher wants to eat, he/she checks both chopsticks. If they are free, then he/she eats. Otherwise, he/she waits on a condition variable. Whenever a philosopher finishes eating, he/she checks to see if his neighbors want to eat and are waiting. If so, then he/she calls signal on their condition variables so that they can recheck the chopsticks and eat if possible.

This is coded up in dphil_5.c. You'll note that we don't keep track of the chopsticks explicitly. Instead, we keep track of the philosophers' states.

A problem with this solution is starvation. For example, trace through dp_5_starve.txt. As you see, after a few seconds, philosophers 0 and 2 get to eat, then 1 and 3, and then 0 and 2 again and so on. Philosopher 4 never gets to eat, because there is never a time when 0 and 3 are both not eating.

In an example with a higher sleep time (dp_5_out.txt), starvation is not a problem, and you'll see that all the threads block for roughly the same amount. Moreover, the total blocking time is similar to dphil_4. Thus, this is a decent solution. It's only problem is that you can get starvation in certain pathological cases.

2100 Total blocktime:  3127 :   577   630   601   709   610

In dphil_5_book.c, I've coded up the book's solution exactly. I think my solution is more readable. If you want some threads practice, make sure you understand how they are functionally equivalent.

Solution #6 -- Preventing starvation

• A guarantee from the thread system that threads will be unblocked from monitors and condition variables in the same order that they are blocked. In such a case, solution #4 will work fine, since a blocked philosopher will then be guaranteed to get a chopstick once it is released. Of course, this doesn't solve the problem that philosopher 4 gets to eat more than the rest, but it does prevent starvation.

• To do it yourself. In other words, you must guarantee that no philosopher may starve. For example, suppose you maintain a queue of philosophers. When a philosopher is hungry, he/she gets put onto the tail of the queue. A philosopher may eat only if he/she is at the head of the queue, and if the chopsticks are free.

Solution #6 dphil_6.c implements this. When a philosopher calls pickup(), if the queue is empty, the chopsticks are checked, and if they are in use, the philosopher is put on the queue. If they are not in use, the philosopher is allowed to eat, and pickup() returns. Note how this checking must be performed in a monitor. When putdown() is called, the chopsticks are released, and then test_queue() is called, which checks the head of the queue to see if the philosopher there can eat. If so, that philosopher is unblocked, and then he/she can eat.

Try the program out to see that it works. Moreover, note that there are times when a philosopher can call pickup() and the sticks can be available, but the philosopher blocks. This is because the queue isn't empty. Thus, the solution may not allow philosophers to eat as much as they would like, but it does prevent starvation. Think about ways that you could prevent starvation, but also allow less blocking time for philosophers.

dp_6_out.txt shows the output of dphil6 5. Note how the total block time here is much higher than dphil_4 and dphil_5. This is because a philosopher might block even though the chopsticks are free, because another philosopher is hungry and on the queue.

2100 Total blocktime:  4441 :   884   887   912   857   901

Solution #7 -- A better try?

So, take a look at dp_7_out.txt.

 2091 Total blocktime:  4231 :   823   848   879   876   805

• 0 eating, 1 waiting, 3 wants to eat (others thinking)
• 0 eating, 4 waiting, 2 wants to eat (others thinking)
• 1 eating, 0 waiting, 3 wants to eat (others thinking)
• 1 eating, 2 waiting, 4 wants to eat (others thinking)
• 2 eating, 1 waiting, 4 wants to eat (others thinking)
• 2 eating, 3 waiting, 0 wants to eat (others thinking)
• 3 eating, 2 waiting, 0 wants to eat (others thinking)
• 3 eating, 4 waiting, 1 wants to eat (others thinking)
• 4 eating, 3 waiting, 1 wants to eat (others thinking)
• 4 eating, 0 waiting, 2 wants to eat (others thinking)

If, however, you increase the number of philosophers to, say, 15, the difference between the two becomes much more drastic. Try running dphil_6 15 10 and dphil_7 15 10 each for a while iterations and compare the total blocked time. Here, waiting philosophers using the dphil_6 algorithm have many more than two in the queue before them, and thus block for a long time. You can see the difference in the performance.

 Dphil_6: 2091 Total blocktime: 19075 :  ...

 Dphil_7: 2100 Total blocktime: 12119 :   ...  

Solution #8 -- The best try

The solution is in dphil_8.c. This looks a lot like dphil_7, but if the chopsticks are available, then it will take them unless one of its neighbors has been waiting for ms*5 or more seconds.

If you call dphil_8 5 1, you'll see that it does not starve any one philosopher as dphil_5 5 1 does. Moreover, if you call dphil_8 5 10, you'll see that its performance overall is good, like dphil_4 and dphil_5, not bad like dphil_7. (The output is in dp_8_out.txt.)

2100 Total blocktime:  2859 :   575   602   538   595   549

Summary of the data

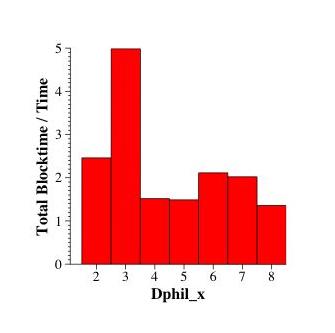
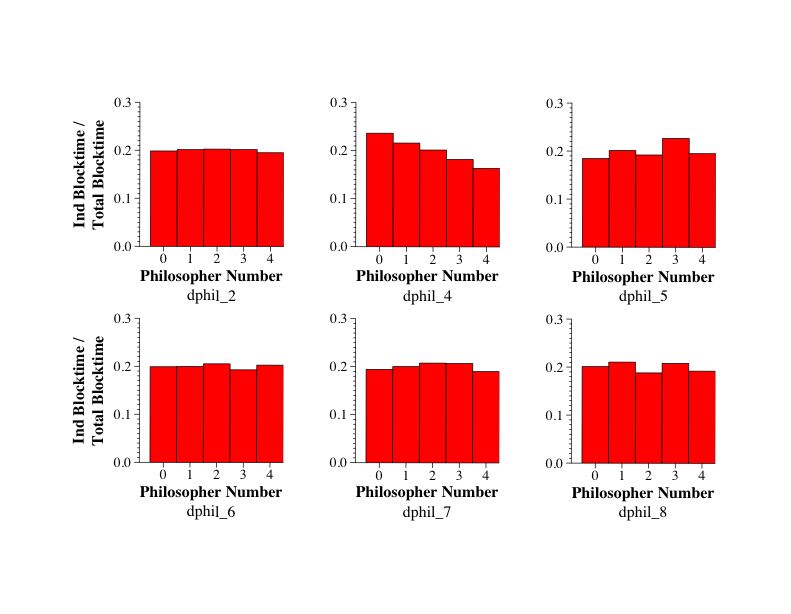
So, what are the lessons?

• First, when multiple threads or processes access multiple resources exclusively, you must worry about deadlock.

• Second, you must worry about starvation, and the only way to prevent starvation is to enforce that all threads/processes get unblocked every now and then. This can be using a global queue, as in solution #6, or some other ordering strategy, as in solutions #7 and #8. Sometimes you have to be less aggressive about preventing starvation (as in solution #8) in order to get both good performance, and no starvation.

• Third, often you have to worry about treating all threads equally, so that no one thread gets more resources than the others due to your synchronization protocol. This was the problem with the asymmetric solution (#4).