





 |
 |
 |
 |
 |
 |
 |
This chapter presents two ADTs: Queues and Priority Queues. In real life a queue is a line of customers waiting for service of some kind. In most cases, the first customer in line is the next customer to be served. There are exceptions, though. For example, at airports customers whose flight is leaving imminently are sometimes taken from the middle of the queue. Also, at supermarkets a polite customer might let someone with only a few items go first.
The rule that determines who goes next is called a queueing discipline. The simplest queueing discipline is called FIFO, for "first-in-first-out." The most general queueing discipline is priority queueing, in which each customer is assigned a priority, and the customer with the highest priority goes first, regardless of the order of arrival. The reason I say this is the most general discipline is that the priority can be based on anything: what time a flight leaves, how many groceries the customer has, or how important the customer is. Of course, not all queueing disciplines are "fair," but fairness is in the eye of the beholder.
The Queue ADT and the Priority Queue ADT have the same set of operations and their interfaces are the same. The difference is in the semantics of the operations: a Queue uses the FIFO policy, and a Priority Queue (as the name suggests) uses the priority queueing policy. Both queue and priority_queue classes are provided in the C++ standard libraries, but with a different interface from the example classes I will develop here.
As with most ADTs, there are a number of ways to implement queues Since a queue is a collection of items, we can use any of the basic mechanisms for storing collections: arrays, lists, or vectors. Our choice among them will be based in part on their performance—how long it takes to perform the operations we want to perform—and partly on ease of implementation.
The queue ADT is defined by the following operations:
To demonstrate a queue implementation, I will take advantage of the LinkedList class from Chapter 18. Also, I will assume that we have a class named Customer that defines all the information about each customer, and the operations we can perform on customers.
As far as our implementation goes, it does not matter what kind of object is in the Queue, so we can make it generic. Here is what the implementation looks like.
template <class ITEMTYPE>A queue object contains a single instance variable, which is the list that implements it. For each of the other methods, all we have to do is invoke one of the methods from the LinkedList class.
An implementation like this is called a veneer. In real life, veneer is a thin coating of good quality wood used in furniture-making to hide lower quality wood underneath. Computer scientists use this metaphor to describe a small piece of code that hides the details of an implementation and provides a simpler, or more standard, interface.
This example demonstrates one of the nice things about a veneer, which is that it is easy to implement, and one of the dangers of using a veneer, which is the performance hazard!
Normally when we invoke a method we are not concerned with the details of its implementation. But there is one "detail" we might want to know—the performance characteristics of the method. How long does it take, as a function of the number of items in the list?
First let's look at removeFirst.
ITEMTYPE removeFirst () {There are no loops or function calls here, so that suggests that the run time of this method is the same every time. Such a method is called a constant time operation. In reality, the method might be slightly faster when the list is empty, since it skips the body of the conditional, but that difference is not significant.
The performance of push_back is very different.
void push_back (ITEMTYPE item) {The first conditional handles the special case of adding a new node to an empty list. In this case, again, the run time does not depend on the length of the list. In the general case, though, we have to traverse the list to find the last element so we can make it refer to the new node.
This traversal takes time proportional to the length of the list. Since the run time is a linear function of the length, we would say that this method is linear time. Compared to constant time, that's very bad.
We would like an implementation of the Queue ADT that can perform all operations in constant time. One way to accomplish that is to implement a linked queue, which is similar to a linked list in the sense that it is made up of zero or more linked Node objects. The difference is that the queue maintains a reference to both the first and the last node, as shown in the figure:
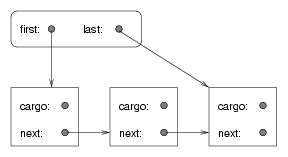
Here's what a linked Queue implementation looks like:
template <class ITEMTYPE>So far it is straightforward. In an empty queue, both first and last are null. To check whether a list is empty, we only have to check one of them.
insert is a little more complicated because we have to deal with several special cases.
void insert (ITEMTYPE item) {The first condition checks to make sure that last refers to a node; if it does then we have to make it refer to the new node.
The second condition deals with the special case where the list was initially empty. In this case both first and last refer to the new node.
remove also deals with several special cases.
ITEMTYPE remove () {The first condition checks whether there were any nodes in the queue. If so, we have to copy the next node into first. The second condition deals with the special case that the list is now empty, in which case we have to make last null.
As an exercise, draw diagrams showing both operations in both the normal case and in the special cases, and convince yourself that they are correct.
Clearly, this implementation is more complicated than the veneer implementation, and it is more difficult to demonstrate that it is correct. The advantage is that we have achieved the goal: both insert and remove are constant time.
Another common implementation of a queue is a circular buffer. "Buffer" is a general name for a temporary storage location, although it often refers to an array, as it does in this case. What it means to say a buffer is "circular" should become clear in a minute.
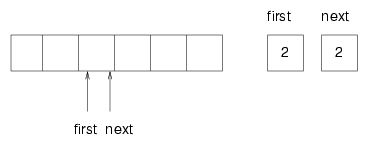
The implementation of a circular buffer is similar to the array implementation of a stack, as in Section 19.7. The queue items are stored in an array, and we use indices to keep track of where we are in the array. In the stack implementation, there was a single index that pointed to the next available space. In the queue implementation, there are two indices: first points to the space in the array that contains the first customer in line and next points to the next available space.
The following figure shows a queue with two items (represented by dots):
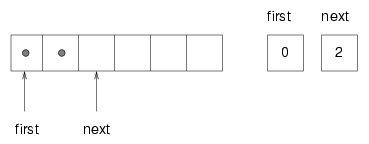
There are two ways to think of the variables first and last. Literally, they are integers, and their values are shown in boxes on the right. Abstractly, though, they are indices of the array, and so they are often drawn as arrows pointing to locations in the array. The arrow representation is convenient, but you should remember that the indices are not references; they are just integers.
Here is an incomplete array implementation of a queue:
template <class ITEMTYPE>The instance variables and the constructor are straightforward, although again we have the problem that we have to choose an arbitrary size for the array. Later we will solve that problem, as we did with the stack, by resizing the array if it gets full.
The implementation of empty is a little surprising. You might have thought that first == 0 would indicate an empty queue, but that neglects the fact that the head of the queue is not necessarily at the beginning of the array. Instead, we know that the queue is empty if head equals next, in which case there are no items left. Once we see the implementation of insert and remove, that situation will more more sense.
void insert (ITEMTYPE item) {insert looks very much like push in Section 19.7; it puts the new item in the next available space and then increments the index.
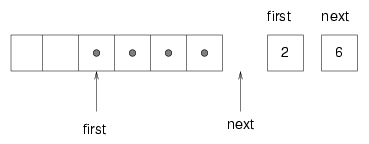
remove is similar. It takes the first item from the queue and then increments first so it refers to the new head of the queue. The following figure shows what the queue looks like after both items have been removed:
It is always true that next points to an available space. If first catches up with next and points to the same space, then first is referring to an "empty" location, and the queue is empty. I put "empty" in quotation marks because it is possible that the location that first points to actually contains a value (we do nothing to ensure that empty locations are initialized); on the other hand, since we know the queue is empty, we will never read this location, so we can think of it, abstractly, as empty.
The next problem with this implementation is that eventually it will run out of space. When we add an item we increment next and when we remove an item we increment first, but we never decrement either. What happens when we get to the end of the array?
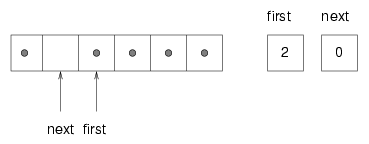
The following figure shows the queue after we add four more items:
The array is now full. There is no "next available space," so there is nowhere for next to point. One possibility is that we could resize the array, as we did with the stack implementation. But in that case the array would keep getting bigger regardless of how many items were actually in queue. A better solution is to wrap around to the beginning of the array and reuse the spaces there. This "wrap around" is the reason this implementation is called a circular buffer.
One way to wrap the index around is to add a special case whenever we increment an index:
next++;A fancy alternative is to use the modulus operator:
next = (next + 1) % array.size();Either way, we have one last problem to solve. How do we know if the queue is really full, meaning that we cannot insert another item? The following figure shows what the queue looks like when it is "full":
There is still one empty space in the array, but the queue is full because if we insert another item, then we have to increment next such that next == first, and in that case it would appear that the queue was empty!
To avoid that, we sacrifice one space in the array. So how can we tell if the queue is full?
if ((next + 1) % array.size() == first)And what should we do if the array is full? In that case resizing the array is probably the only option.
As an exercise, put together all the code from this section and write an implementation of a queue using a circular buffer that resizes itself when necessary.
The Priority Queue ADT has the same interface as the Queue ADT, but different semantics. The interface is:
The semantic difference is that the item that is removed from the queue is not necessarily the first one that was added. Rather, it is whatever item in the queue has the highest priority. What the priorities are, and how they compare to each other, are not specified by the Priority Queue implementation. It depends on what the items are that are in the queue.
For example, if the items in the queue have names, we might choose them in alphabetical order. If they are bowling scores, we might choose from highest to lowest, but if they are golf scores, we would go from lowest to highest.
So we face a new problem. We would like an implementation of Priority Queue that is generic—it should work with any kind of object—but at the same time the code that implements Priority Queue needs to have the ability to compare the objects it contains.
We have seen a way to implement generic data structures using Node, but that does not solve this problem, because there is no way to compare Node unless we know what type the cargo is. So basically, to implement a priority queue, we will have to create compare functions that will compare the cargo of the nodes.
In the implementation of the Priority Queue, every time we specify the type of the items in the queue, we specify the type of the cargo. For example, the instance variables are an array of Node and an integer:
template <class ITEMTYPE>As usual, index is the index of the next available location in the array. The instance variables are declared private so that other classes cannot have direct access to them.
The constructor and empty are similar to what we have seen before. I chose the initial size for the array arbitrarily.
public:insert is similar to push:
void insert (ITEMTYPE item) {I omitted the implementation of resize. The only substantial method in the class is remove, which has to traverse the array to find and remove the largest item:
ITEMTYPE remove () {As we traverse the array, maxIndex keeps track of the index of the largest element we have seen so far. What it means to be the "largest" is determined by >.
As an example of something with an unusual definition of "highest" priority, we'll use golfers:
class Golfer {The class definition and the constructors are pretty much the same as always.
Since priority queues require some comparisons, we'll have to overload the > operator. So let's write one:
bool operator > (Golfer g1, Golfer g2) {Finally, we can create some golfers:
Golfer tiger = Golfer ("Tiger Woods", 61);And put them in the queue:
PriorityQueue<Golfer> pq;When we pull them out:
while (!pq.empty ()) {They appear in descending order (for golfers):
Tiger Woods 61Ok, so now that we've got a priority queue done for golfers… FORE!!!
Revised 2008-12-11.
 |
 |
 |
 |
 |
 |
 |