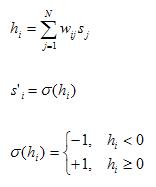Project 3 — Hopfield Net
COSC 420 portion
Randomly initialize 50 vectors, each with 100 elements, where each
element is 1 or -1.
Then loop through each of these p patterns (vectors) and do the
following:
1. Imprint patterns 1 through p (p above loops from 1 to 50).
This is where you compute the various weights associated with the
neurons, which you will use to calculate the net input (local field)
in a later step. The formula for computing the weights is given by:

This will calculate the weight associated with neurons i and j,
where i and j each range from 1 to 100 (or 0 to 99, depending on
your array indexing scheme). So each weight represents a pair of
neurons. This implies you will have a 100x100 array of weights. The
index k loops through each of the patterns 1 through p. The si
and sj represent the state values (1 or -1) for neurons i
and j, respectively. So you will take the product of the state
values of neurons i and j for pattern k, and sum over the p
imprinted patterns. Then simply divide this number by the number of
neurons N (100). This assumes that i and j are not equal. If i and j
are equal, then just assign the corresponding weight to 0. This is
what is meant by no self-coupling, a neuron does not have a weight
associated with itself.
2. Test the p imprinted patterns for stability. Here is where
you will determine the number and fraction of imprints that are
stable (or unstable). For each of the p patterns, do:
a. Set the neural net (100 element array) to that pattern.
b. For each of the 100 neurons, first compute its new state value
using the following formulas:
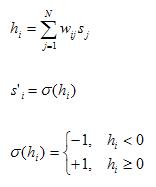
The first formula computes the local field of the neuron. The
variable j iterates through each neuron of the neural net (100
element array), and multiplies the neuron's state value with its
associated weight matrix value. The variable i represents the
current neuron being considered at the beginning of step b, so we
are interested in row i of the weight matrix.
The other two formulas determine the next state of the current
neuron, -1 if its local field h is negative, and +1 if its local
field h is nonnegative.
After getting the neuron's new state, compare it to the neuron's
current state (the values you assigned to the neural net in step a).
If any of the 100 elements of the neural net differ from its
corresponding new state value, then that imprinted pattern that was
assigned to the neural net is NOT stable. Otherwise, if each element
matches its new state based on the local field computation, then
that imprinted pattern IS stable.
c. Keep a counter of how many of these imprinted patterns is stable
for each value p. You can keep track of each counter with an array
of 50 elements (one for each p).
d. To compute the probability of stable imprints for each p, just
divide the number of stable imprints for that p by that number p. To
get the probability of UNstable imprints for that p, subtract the
probability of stable imprints for that p from 1.
3. Generate data for the following two graphs:
a. The fraction of unstable imprints as a function of the number of
imprints (p=1 to 50)

b. The number of stable imprints as a function of the number of
imprints (p=1 to 50)
You can just write the data to a .csv file, and then use Excel to
create the graphs. Your program does not have to produce the graphs
themselves, just the data for the graphs. The data will consist of
the number p, the number of stable imprints for that p, and the
fraction of unstable imprints for that p. Again, p ranges from 1 to
50.
Repeat steps 1 and 2 several times, each time testing a different
set of 50 random patterns (vectors). Average your data over all of
these iterations.
COSC 427/527 portion:
In addition to the undergrad portion, estimate the size of the
basins of attraction for each imprinted pattern of each value of p.
In the part above where you test for stability of each of the p
imprinted patterns, add the following:
1. If the pattern is unstable, set its basin size to 0.
2. If the pattern is stable, do:
a. Generate a permutation of the numbers 1 to 100 by creating an
array of the numbers 1 to 100 in random order. This list of numbers
will indicate which bits of the pattern to flip and in which order
to flip them. You will only need to consider the first 50 elements
of this permutation since the maximum basin size is 50.
b. Letting i be the loop variable, go through each of the first 50
elements in the permutation array and:
i. Initialize the neural network to the current pattern of the p
imprinted patterns.
ii. Flip the states of the positions of the neural network given by
the first i permutation array elements. That is, change a 1 to a -1
and a -1 to a 1 in these i positions of the neural network.
iii. Go through 10 iterations of updating the neural network. Change
each network element according to sigma of its local field h.
iv. Check to see if the network is equal to the current imprinted
pattern after these 10 iterations.
c. The first iteration of the permutation array (as given by i)
where the network does not converge to the current imprinted pattern
is the number that estimates the size of the basin of attraction for
that imprinted pattern. It is equivalent to the number of bits in
the pattern you need to flip until the network does not converge to
that pattern. If the network converges for all 50 iterations of the
permutation array (that is, it never doesn't converge), then let the
size of the basin of attraction for that pattern be 50, since that
is the maximum size of a basin of attraction.
Try the above a-c for several different permutations and average the
results.
3. Increment the counter of the array keeping track of the basin
sizes. You might have a two dimensional array where the first
dimension indicates the number of imprinted patterns, and the second
dimension gives the size of the basin of attraction. This will keep
track of a histogram of basin sizes for each value p.
4. Produce a graph of the histograms for various values of p
(even values of p should be enough) as in the following:
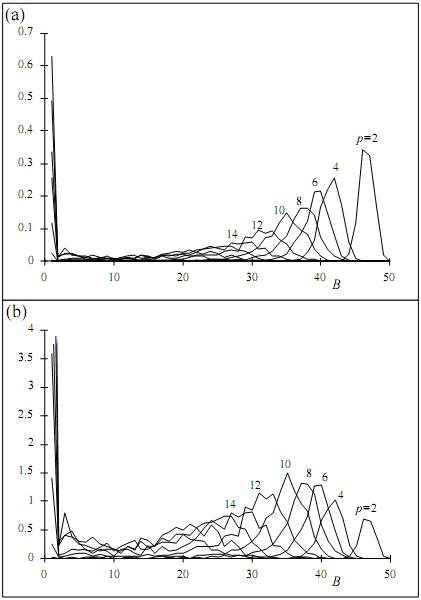
For normalizing the data, keep in mind the number of permutations
you try, and the number of different sets of 50 patterns you try.