 |
- Node - Edge - Binary - Complete - Parent - Child - Ancestor - Descendent - Root - Leaf - Internal - External - Height of node or tree - Depth of node - Degree
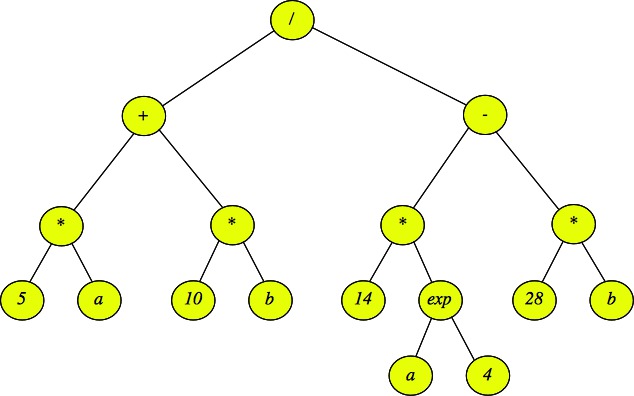
Trees are often a very natural way to represent hierarchies. For example, the mathematical expression:
 |
Using tree terminology, the external, (or leaf) nodes are either variables or values, and the internal nodes are operators.
Pre-OrderTo visit a node:
Example on the above tree: Print "/" Print "+" Print "*" Print "5" Print "a" Print "*" Print "10" Print "b" Print "-" Print "*" Print "14" Print "exp" Print "a" Print "4" Print "*" Print "28" Print "b" |
Post-OrderTo visit a node:
Example on the above tree: Print "5" Print "a" Print "*" Print "10" Print "b" Print "*" Print "+" Print "14" Print "a" Print "4" Print "exp" Print "*" Print "28" Print "b" Print "*" Print "-" Print "/" |
In-Order (Binary only)To visit a node:
Example on the above tree: Print "5" Print "*" Print "a" Print "+" Print "10" Print "*" Print "b" Print "/" Print "14" Print "*" Print "a" Print "exp" Print "4" Print "-" Print "28" Print "*" Print "b" |
Example Question: "Which of the above traversals would allow you to evaluate the expression of the above tree?"
Answer: A post-order traversal -- for each operator in an internal node, you need to first evaluate each of its children before you can perform the operation. For example, you need to evaluate the left subtree of "/" and then the right subtree before you divide the two answers to get the final evaluation of the expression.
In class, I'll go over http://web.eecs.utk.edu/~jplank/topcoder-writeups/Leetcode/Minimum-Fuel-Cost-Capital/index.html, which is a Leetcode problem featuring a postorder traversal, and http://web.eecs.utk.edu/~jplank/topcoder-writeups/Leetcode/Sum-Root-To-Leaf-Numbers/index.html, which is a Leetcode problem featuring a preorder traversal.
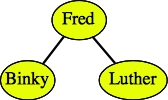
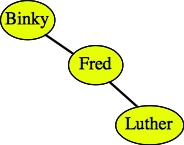
Here are some examples of binary search trees that hold strings:
 |
 |
 |
 |
As demonstrated by the second two trees above, there can be more than one binary search tree that corresponds to the same data.
Here are two examples of trees that are not binary search trees:
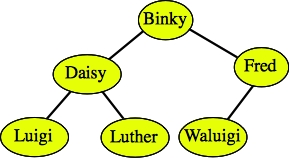 Daisy, Luigi and Luther are all greater than Binky. |
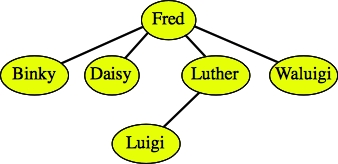 The tree is not binary. |
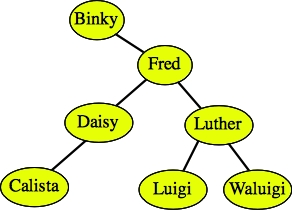
Binary search trees have nice properties. For example, you can sort the data by performing an in-order traversal. You can also find a piece of data simply by traversing a single path from the root to the data, or to where the data would be. For example, in the tree:
 |
If I want to find Luigi, what I do is start at the root of the tree, and compare it to Luigi. If it equals Luigi, then I'm done. If not, and Luigi is less than the node's value, then I recursively continue the process on the tree's left child. If Luigi is greater than the node's value, then I instead recursively continue the process on the tree's right child. If I ever get to a point where the node has no child for me to search on, I can conclude that the value is not in the tree.
Continuing the example of finding Luigi, I would:
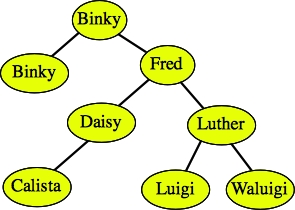
For example, suppose that we want to insert Calista into the above tree. We try to find the string as we did above. We fail at Daisy's left child, which doesn't exist. Therefore, we create a node for Calista and insert it as Daisy's left child:
 |
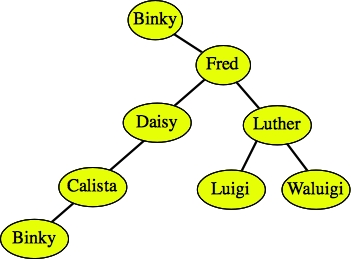
To insert duplicate values, do the same procedure, only if you find the value, you continue searching either on the left or the right child, as if you didn't find the key. For example, if you wanted to insert Binky into the tree again, you would either put it as Binky's left child or Calista's left child:
 |
 |
Deletion is the trickiest. To delete a node, you must consider three cases. Let's consider the tree below as an example:
 |
Case 1: The node has no children (it's a leaf node). You can simply delete it. I won't draw an example, but you should see very easily that deleting Calista, Luigi or Waluigi just removes them from the tree.
Case 2: The node has just one child. To delete the node, replace it with that child. I draw two examples below:
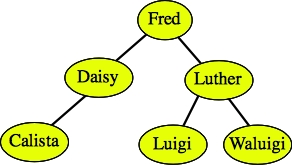 After deleting Binky. |
 After deleting Daisy. |
Case 3: The node has two children. In this case, you find the node in the tree whose value is the greatest value less than (or equal to) the node's value. That will be the rightmost node in the subtree rooted by the left child. That node will not have a right child. First, delete it. Then use it to replace the node that you are deleting.
Alternatively, you can replace it with the leftmost node in the tree rooted by the node's right child. Both will work.
For example, let's delete Fred from the tree below:
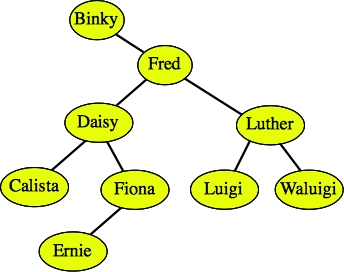 |
Since Fred has two children, we find the rightmost node in the tree rooted by Fred's left child. That is the node Fiona. We first delete Fiona:
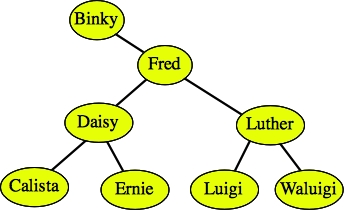 |
And then we replace Fred with Fiona:
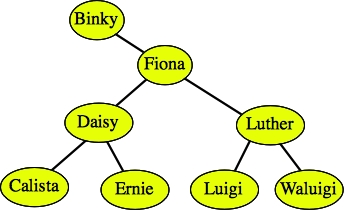 |
A second example is easier, but sometimes confusing -- suppose we want to delete Luther. Since Luther has two children, we find the rightmost node in the tree rooted by Luther's left child. Since there is only one node in that tree, that's the one we delete: Luigi. We then replace Luther with Luigi:
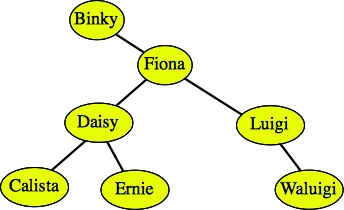 |
#include <vector>
#include <string>
namespace CS202 {
/* These are the nodes of a tree. The keys are strings, and the vals are generic pointers.
Please see the lecture notes for a more thorough explanation of what a (void *) is. */
class BSTNode {
friend class BSTree;
protected:
BSTNode *left;
BSTNode *right;
BSTNode *parent;
std::string key;
void *val;
};
class BSTree {
public:
/* Constructor, copy constructor, assignment overlead, destructor.
I am only implementing the constructor and destructor here in the notes.
You will implement the other two in your lab. */
BSTree();
BSTree(const BSTree &t);
BSTree& operator= (const BSTree &t);
~BSTree();
void Clear(); // Turns the tree into an empty tree.
void Print() const; // These are obvious.
size_t Size() const;
bool Empty() const;
bool Insert(const std::string &key, void *val); // Insert the key and val. Returns success (duplicates are not allowed.
void *Find(const std::string &key) const; // Return the val associated with the key. Returns NULL if key not found.
bool Delete(const std::string &key); // Delete the node with the key. Returns whether there was such a node.
std::vector <std::string> Ordered_Keys() const; // Return a vector of sorted keys
std::vector <void *> Ordered_Vals() const; // Return a vector of the vals, sorted by the keys.
/* You'll write these as part of your lab. */
int Depth(const std::string &key) const; // Distance from a node to the root. Returns -1 if the key is not in the tree.
int Height() const; // Returns the depth of the node with maximum depth, plus one.
protected:
BSTNode *sentinel; // Like the dlists, there is a sentinel. Its right points to the root.
size_t size; // Size of the tree
void recursive_inorder_print(int level, const BSTNode *n) const; // A helper for Print()
void recursive_destroy(BSTNode *n); // A helper for Clear()
void make_val_vector(const BSTNode *n, std::vector<void *> &v) const; // A helper for Ordered_Vals()
/* You'll write these as part of your lab. */
int recursive_find_height(const BSTNode *n) const; // A helper for Height()
void make_key_vector(const BSTNode *n, std::vector<std::string> &v) const; // A helper for Ordered_Keys()
BSTNode *make_balanced_tree(const std::vector<std::string> &sorted_keys, // A helper for the copy constructor and assignment overload.
const std::vector<void *> &vals,
size_t first_index,
size_t num_indices) const;
};
};
|
First off, you'll note I'm using a "namespace". It's about time that I introduce you to namespaces. They are pretty simple -- when you define a class (or struct), global variable, or procedure within a namespace, then when someone else wants to use it, they need to either:
BSTree *t1, *t2, *tmp; |
If I didn't put the "using" statement in there, I'd have to declare the pointers as:
CS202::BSTree *t1, *t2, *tmp; |
Namespaces are nice because they help you avoid conflicts in naming. I won't go crazy with them, but I do think they are something you should see and know about at this point in your programming careers.
Now, the BSTree API is a little like the Dlist API in the previous lecture, with some extra bells and whistles. Let's first go over the methods:
Person *p; |
And suppose you want to insert the key "Fred" and the val p into a tree t. Then you would do it as follows:
t.Insert("Fred", (void *) p);
|
The "(void *) p" part tells the compiler "I know you want a (void *) and I'm giving you a (Person *). It's all good." If you don't put the "(void *)" in, the compiler will yell at you.
I use the (void *) for flexibility -- it allows me to store any pointer in the val field. The STL does the same thing using templates, and it is superior to a (void *) in most respects. I will teach you templates later in the class. Using a (void *) is an "old school" C trick, which I'm using here for convenience.
Insert() returns whether the key was inserted. We're going to disallow inserting duplicate keys, so Insert() will return false if it gets a duplicate key.
p = (Person *) Find("Fred");
|
If the key is not found, then Find() returns NULL. Does that mean that you can't store NULL in the tree? You tell me.
There is a testing program in bstree_test.cpp. It's a standard command line tool for managing a tree of Persons:
class Person {
public:
string name;
string phone;
string ssn;
void Print() const;
};
|
You run it with a prompt on the command line ("-" for no prompt), and it accepts lines of commands on standard input. You can see the commands when you enter a question mark:
UNIX> echo '?' | bin/bstree_tester usage: bstree_tester prompt(- for empty) -- commands on stdin. commands: INSERT name phone ssn - Insert the person into the tree. FIND name - Find the person and print them out. DELETE person - Delete the person. PRINT - Print the keys using the Print() method. EMPTY - Print whether the tree is empty. SIZE - Print the tree's size. HEIGHT - Print the tree's height. DEPTH name - Print the depth of the node whose key is name (-1 if not there). KEYS - Print the keys using the Ordered_Keys() method. VALS - Print the vals using the Ordered_Vals() method. PRINT_COPY - Call the copy constructor and call its Print() method. REBALANCE - Turn the tree into a balanced tree by calling the assignment overload. CLEAR - Clear the tree back to an empty tree. DESTROY - Call the destructor and remake an empty tree. QUIT - Quit. ? - Print commands. UNIX>Here I'll show some INSERT, FIND, DELETE, KEYS and VALS commands:
UNIX> bin/bstree_tester 'BST>' BST> INSERT Jim-Plank 865-123-4567 111-11-1111 # I'll insert three people BST> INSERT Harvey-Plank 026-631-5520 826-96-9094 BST> INSERT Abba 462-055-3150 827-30-6292 BST> FIND Abba # Find returns the Person, which we print. Abba 462-055-3150 827-30-6292 BST> KEYS # KEYS returns a vector of sorted keys, which we print Abba Harvey-Plank Jim-Plank BST> VALS # VALS returns the vals pointers, in the order of the keys. Abba 462-055-3150 827-30-6292 # bstree_tester.cpp prints these vals. Harvey-Plank 026-631-5520 826-96-9094 Jim-Plank 865-123-4567 111-11-1111 BST> FIND Fred # FIND returns NULL when you can't find something. Not found. # bstree_tester.cpp prints "Not found." when this happpens. BST> DELETE Abba # Here, we delete "Abba". BST> VALS Harvey-Plank 026-631-5520 826-96-9094 Jim-Plank 865-123-4567 111-11-1111 BST> FIND Abba Not found. BST> QUIT UNIX>Take a look at how the code that inserts people into the tree. Each line of input is put into the vector sv of the individual words on a line. This shows how we cast to a (void *) when we call Insert():
/* With the INSERT command, we create a Person, and then insert it into the tree with
the name as its key, and a pointer to the person (cast as a (void *)) as its val. */
} else if (sv[0] == "INSERT") {
if (sv.size() != 4) {
cout << "usage: INSERT name phone ssn" << endl;
} else {
p = new Person;
p->name = sv[1];
p->phone = sv[2];
p->ssn = sv[3];
if (!t1->Insert(p->name, (void *) p)) { /* Here's where we cast to a (void *) */
cout << "Insert " << p->name << " failed." << endl;
delete p;
}
}
|
And below, I show how Find() returns a (void *), but it is cast to a (Person *) for printing.
/* The Find() method returns a (void *), so I must typecast it to a (Person *) */
} else if (sv[0] == "FIND") {
if (sv.size() != 2) {
cout << "usage: FIND key" << endl;
} else {
p = (Person *) t1->Find(sv[1]); /* Here is where we typecast the (void *) to a (Person *). */
if (p == NULL) {
cout << "Not found.\n";
} else {
p->Print();
}
}
|
And finally, take a look at how src/bstree_tester.cpp gets all of the vals in the tree by calling Ordered_Vals(). This is an array of (void *)'s, so each of these must be typecast to a (Person *) to print:
/* The VALS command calls Ordered_Vals() to get a vector of (void *)'s.
We typecast each to a (Person *) and then print the person. */
} else if (sv[0] == "VALS") {
vals = t1->Ordered_Vals();
for (i = 0; i < vals.size(); i++) {
p = (Person *) vals[i];
p->Print();
}
|
UNIX> bin/bstree_tester '--------->'
---------> INSERT Binky 944-867-2246 165-79-8849
---------> INSERT Fred 026-631-5520 826-96-9094
---------> INSERT Luther 462-055-3150 827-30-6292
---------> INSERT Waluigi 193-149-4333 106-62-2934
---------> INSERT Daisy 257-554-8530 481-12-6340
---------> INSERT Luigi 018-992-9715 512-23-5507
---------> INSERT Ernie 808-602-6582 702-11-9340
---------> INSERT Calista 457-440-4397 076-91-9105
---------> PRINT # This is the same tree as above
Waluigi
Luther
Luigi
Fred
Ernie
Daisy
Calista
Binky
---------> INSERT Alvin 345-654-3434 242-55-4444
---------> PRINT # Alvin will be inserted as Binky's left child.
Waluigi
Luther
Luigi
Fred
Ernie
Daisy
Calista
Binky
Alvin
---------> DELETE Luigi # Luigi has no children, so deleting him is easy
---------> PRINT
Waluigi
Luther
Fred
Ernie
Daisy
Calista
Binky
Alvin
---------> DELETE Luther # Luther has one child, so we replace him with his child (Waluigi)
---------> PRINT
Waluigi
Fred
Ernie
Daisy
Calista
Binky
Alvin
---------> DELETE Fred # Fred has two children, so we find the node with the
---------> PRINT # greatest key in his left subtree, which is Ernie,
Waluigi # replace Fred's key and val with Ernie's key and val,
Ernie # and delete Ernie.
Daisy
Calista
Binky
Alvin
---------> DEPTH Binky # Binky is the root, which has a depth of 0
0
---------> DEPTH Daisy # Daisy is two edges from the root.
2
---------> DEPTH Calista # And Caliste is three.
3
---------> HEIGHT # Calista has the greatest depth in the tree, so the
4 # height of the tree is Calista's depth plus one.
---------> QUIT
UNIX>
class BSTNode {
friend class BSTree;
protected:
BSTNode *left;
BSTNode *right;
BSTNode *parent;
string key;
void *val;
};
|
Besides storing a key and a val, each BSTNode contains a pointer to its left child, right child and parent. As with the Dlist, we are going to have a sentinel node that simplifies the code. The only part of the sentinel that we're going to use is its right pointer. That is going to point to the root of the tree. Rather than point to NULL, pointers that should point to nothing will point to the sentinel. Thus, when we create the following tree:
UNIX> bstree_test - INSERT Fred 026-631-5520 826-96-9094 INSERT Binky 944-867-2246 165-79-8849 INSERT Luigi 462-055-3150 827-30-6292 QUIT UNIX>It is going to have the following representation:
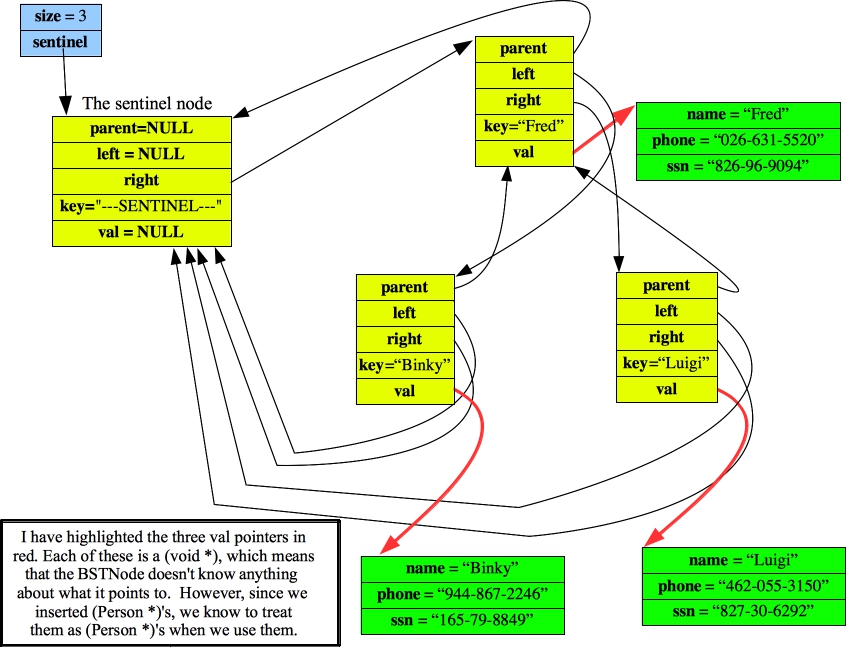 |
The constructor, size() and Empty() are straightforward as usual. The empty tree has sentinel->right point to sentinel:
BSTree::BSTree()
{
sentinel = new BSTNode;
sentinel->parent = NULL;
sentinel->left = NULL;
sentinel->right = sentinel;
sentinel->key = "---SENTINEL---"; // This helps with debugging.
sentinel->val = NULL;
size = 0;
}
|
bool BSTree::Size() const
{
return size;
}
|
bool BSTree::Empty() const
{
return (size == 0);
}
|
The implementation of Find() is a simple while loop that either finds the key or returns NULL when the sentinel has been reached:
/* This is a standard search on a binary search tree. */
void *BSTree::Find(const string &key) const
{
BSTNode *n;
n = sentinel->right;
while (1) {
if (n == sentinel) return NULL;
if (key == n->key) return n->val;
n = (key < n->key) ? n->left : n->right;
}
}
|
Insert() starts similarly to Find(). If it actually finds the key, then it returns false. Otherwise, the important thing is finding the parent of the newly created node. Once the parent is found, the new node is created, its left and right pointers are set to be the sentinel, and its parent pointer is set to be its parent. At this point, all of its pointers are correct -- the only thing that needs to be fixed is the parent -- the new node is either the parent's left or right child. Once that is figured out, the pointer is set, and we return true:
bool BSTree::Insert(const string &key, void *val)
{
BSTNode *parent;
BSTNode *n;
parent = sentinel;
n = sentinel->right;
/* Find where the key should go. If you find the key, return false. */
while (n != sentinel) {
if (n->key == key) return false;
parent = n;
n = (key < n->key) ? n->left : n->right;
}
/* At this point, parent is the node that will be the parent of the new node.
Create the new node, and hook it in. */
n = new BSTNode;
n->key = key;
n->val = val;
n->parent = parent;
n->left = sentinel;
n->right = sentinel;
/* Use the correct pointer in the parent to point to the new node. */
if (parent == sentinel) {
sentinel->right = n;
} else if (key < parent->key) {
parent->left = n;
} else {
parent->right = n;
}
/* Increment the size and return success. */
size++;
return true;
}
|
The tough code is Delete(). The first thing that we have to do is find the node. Once we do, we consider the three cases that are described above. If the node has no left child, then we replace the node with its right child. The way we "replace" the node is we set the parent's link to that node to equal the right child. Otherwise, if the node has no right child, then we replace it with its left child.
Those are the easy cases. The hard case is when the node has two children. In that case, we find the maximum node whose key is less than the node's key (There are no duplicates, which simplifies matters). This node is in the variable mlc. We recursively delete mlc, and then replace n's key and val with mlc's key and val:
bool BSTree::Delete(const string &key)
{
BSTNode *n, *parent, *mlc;
string tmpkey;
void *tmpval;
/* Try to find the key -- if you can't, return false. */
n = sentinel->right;
while (n != sentinel && key != n->key) {
n = (key < n->key) ? n->left : n->right;
}
if (n == sentinel) return false;
/* We go through three cases for deletion. */
parent = n->parent;
/* Case 1 - I have no left child. Replace me with my right child.
Note that this handles the case of having no children, too. */
if (n->left == sentinel) {
if (n == parent->left) {
parent->left = n->right;
} else {
parent->right = n->right;
}
if (n->right != sentinel) n->right->parent = parent;
delete n;
size--;
/* Case 2 - I have no right child. Replace me with my left child. */
} else if (n->right == sentinel) {
if (n == parent->left) {
parent->left = n->left;
} else {
parent->right = n->left;
}
n->left->parent = parent;
delete n;
size--;
/* If I have two children, then find the node "before" me in the tree.
That node will have no right child, so I can recursively delete it.
When I'm done, I'll replace the key and val of n with the key and
val of the deleted node. You'll note that the recursive call
updates the size, so you don't have to do it here. */
} else {
for (mlc = n->left; mlc->right != sentinel; mlc = mlc->right) ;
tmpkey = mlc->key;
tmpval = mlc->val;
Delete(tmpkey);
n->key = tmpkey;
n->val = tmpval;
}
return true;
}
|
We need to be really careful making that recursive call. If we set n->key equal to tmpkey before making the recursive call, we'd delete the wrong node. Also, since the recursive call deletes mlc, we can't use it following the recursive call -- this is why we stored mlc->key and mlc->val in tmpkey and tmpval. Finally, since the recursive call decreases the size, we don't do it here.
The last calls are the traversals. We do these recursively with protected methods (we don't want to let others make these calls -- they are just for us). Start with Print() -- it calls recursive_inorder_print() on the root of the tree (in sentinel->right). Recursive_inorder_print() does an in-order traversal in reverse order -- it calls itself recursively on its right child, then it prints the node, and finally it calls recursively on its left child. It always stops when it reaches the sentinel.
/* Print() simply calls recursive_inorder_print() on the root node of the tree. */
void BSTree::Print() const
{
recursive_inorder_print(0, sentinel->right);
}
/* This does an inorder traversal in reverse order. The "Action" is printing "level" spaces,
and then the key. You increment the level by two when you make recursive calls. */
void BSTree::recursive_inorder_print(int level, const BSTNode *n) const
{
if (n == sentinel) return;
recursive_inorder_print(level+2, n->right);
printf("%*s%s\n", level, "", n->key.c_str());
recursive_inorder_print(level+2, n->left);
}
|
The other two recursive traversals are Ordered_Vals and Clear(). The first performs an in-order traversal, pushing vals onto a vector, while the second performs a post-order traversal, deleting nodes of the tree. The post-order traversal is necessary, because we can't use n->left or n->right after we've deleted n. Granted, we could store them in temporary pointers, delete n and then recursively delete the temporary pointers, but the post-order traversal is easier.
/* This simply calls make_val_vector() on the root.
That creates the vector rv, so return it. */
vector <void *> BSTree::Ordered_Vals() const
{
vector <void *> rv;
make_val_vector(sentinel->right, rv);
return rv;
}
/* This does an inorder traversal, which of course visits the nodes
in sorted order of the keys. The "action" is pushing the val onto the vector.
That means that the vals get pushed in the correct order. */
void BSTree::make_val_vector(const BSTNode *n, vector<void *> &v) const
{
if (n == sentinel) return;
make_val_vector(n->left, v);
v.push_back(n->val);
make_val_vector(n->right, v);
}
/* Clear simply calls recursive_destroy on the root of the tree.
That deletes all of the nodes but the sentinel. It then sets
the root of the tree to the sentinel and the size to 0. */
void BSTree::Clear()
{
recursive_destroy(sentinel->right);
sentinel->right = sentinel;
size = 0;
}
/* Recursive destroy deletes all of the nodes of a tree.
It does this with a postorder traversal -- deleting the
children before deleting the node. */
void BSTree::recursive_destroy(BSTNode *n)
{
if (n == sentinel) return;
recursive_destroy(n->left);
recursive_destroy(n->right);
delete n;
}
/* The destructor calls Clear(), which deletes all of the tree but
the sentinel node. Therefore, it must also delete the sentinel node. */
BSTree::~BSTree()
{
Clear();
delete sentinel;
}
|
A final comment on the destructor. Should it also delete the val's? The answer is no -- it's good form only to delete what you create with new. What if the user of this data structure didn't create the val's with new, or what if the user is holding them in a second data structure? Then it would be really bad form for the destructor to delete it!
The assignment overload and copy constructor are necessary. The reason is that without them, you'd simply copy the size and the sentinel pointer, and now you'd have two trees pointing to the same sentinel. When one of them calls its destructor, then the second one will be pointing to deleted memory - a disaster!
With this data structure, we are making the assignment overload and copy constructor special. Not only do they make a copy of the tree, but they make the new copy balanced. The reason is that it will improve the performance of subsequent Insert(), Find() and Delete() operations. Let's take an example -- in src/bstree_tester.cpp, the PRINT_COPY command calls a procedure called print_copy() with the tree as a parameter. This will call the copy constructor, so that print_copy() gets a copy of the original tree. This copy will be balanced (the original tree will remain unchanged) -- read the inline comments:
UNIX> bin/bstree_tester '--------->' # We insert 0 through 6 in order,
---------> INSERT 0 0 0 # which means that our tree is a big line.
---------> INSERT 1 0 0
---------> INSERT 2 0 0
---------> INSERT 3 0 0
---------> INSERT 4 0 0
---------> INSERT 5 0 0
---------> INSERT 6 0 0
---------> PRINT
6
5
4
3
2
1
0
---------> PRINT_COPY # PRINT_COPY calls the copy constructor,
6 # which creates a balanced version of the tree.
5 # Since 3 is the middle key, it becomes the root
4 # of the tree. Its left subtree has the values
3 # 0, 1 and 2. Since 1 is the middle of these,
2 # it is the root of the subtree. Similarly, the
1 # right subtree has the values 4, 5, and 6, so
0 # 5 is the root of the subtree.
---------> PRINT
6 # I'm doing this to show you that the original
5 # tree is unmodified. Only the copy was balanced.
4
3
2
1
0
---------> QUIT
UNIX>
The assignment overload also balances. In
src/bstree_tester.cpp, the command "REBALANCE"
calls the assignment overload and sets the main tree pointer to be this new tree.
That way, it balances the tree. I'm going to show that below. Also, make note of the
fact that when a tree has an even number of elements, then there are two potential "middle"
elements. The code here chooses the higher of the two elements. I'll show that below.
Your code will have to do this:
UNIX> bin/bstree_tester '--------->'
---------> INSERT 0 0 0 # I make a big line again, this time with 8 elements
---------> INSERT 1 0 0
---------> INSERT 2 0 0
---------> INSERT 3 0 0
---------> INSERT 4 0 0
---------> INSERT 5 0 0
---------> INSERT 6 0 0
---------> INSERT 7 0 0
---------> PRINT
7
6
5
4
3
2
1
0
---------> REBALANCE
---------> PRINT
7
6
5
4 # Since there are 8 elements in the tree, there are two potential middles. We choose the larger: 4
3
2 # This subtree has four elements, so there are two potential middles. We choose the larger: 2
1 # This subtree has two elements, so there are two potential middles. We choose the larger: 1
0
---------> QUIT
UNIX>
I'll give an example. Suppose the keys are "0" through "6" as above. Then here are the calls to make_balanced_tree():
For general trees, you should know the following things: