 |
These will be specified by strings, one per die, that contain the letters on the die. We won't constrain dice to have six sides -- we'll assume that a die may have any number of sides, and that the length of the string defines the number of sides on a die.
For example, let's assume that the above dice only have three sides each -- the sides that you can see. Then, the file Dice1.txt defines the four dice pictured:
ENG SAA PRR EAE |
Now, you are also given a list of words, and your job is to spell the words on the dice so that each letter of the word is on a different die. For example, "RAGE" may be spelled using 'R' from the "PRR" die, 'A' from the "SAA" die, 'G' from the "ENG" die and 'E' from the "EAE" die. Similarly, "SEEP" may be spelled with 'S' from the "SAA" die, 'E' from the "EAE" die, 'E' from the "ENG" die and 'P' from the "PRR" die. However, you cannot spell "PEEN", even though all the letters are there, because you would have to use the "ENG" die for both the 'E' and 'N'.
Your job is to write the program worddice, called as follows:
worddice dice-file word-list |
The dice file is a list of dice as above. Each die may have any number of letters, and within a file, the dice may all have differing numbers of letters. The word list is a file that contains words. For each word in the word list file, your program should print out:
- If the word cannot be spelled: "Cannot spell word".
- If the word can be spelled: The order of the dice used to spell out the word, then the word. The dice are numbered starting with zero.
UNIX> cat Dice1.txt ENG SAA PRR EAE UNIX> cat Words1.txt RAGE SEEP ERR PEEN GASP UNIX> worddice Dice1.txt Words1.txt 2,1,0,3: RAGE 1,0,3,2: SEEP Cannot spell ERR Cannot spell PEEN 0,3,1,2: GASP UNIX>
Organizing the program
This is an example of a bipartite matching. For each word, set up a graph that matches dice to letters of the words. For example, here are the above dice with the word "RAGE":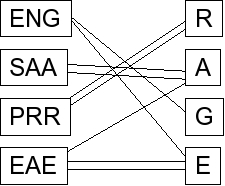 |
I've included double-edges for the duplicate letters. Your program can eliminate these if you want, since duplicate letters don't help you at all and just make your program run slower. My program does that. You want to find a matching of this graph that is composed of edges that connect two nodes, where no edge is incident to the same node.
To do this, you convert the graph into one in which network flow will solve the problem: a source node connected to each die, and a sink node connected to each letter of the word:
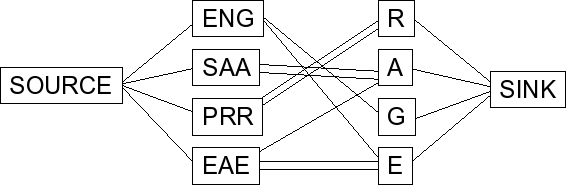 |
Finding the maximum flow will discover the matching if it exists. Here is the flow/matching in this example:
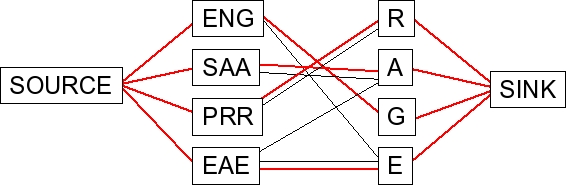 |
Your program should use the Edmonds-Karp algorithm to determine maximum flow. The fact that all edges have weight one makes this easier.
My program is slow for two reasons. First, I create and destroy the graph with each word. It would be faster if I never deleted the source and dice nodes/edges. Second, when I create the edges to each letter of the word, I use the Find() method on the dice strings. That is inefficient as I could instead have a 256-element array for each die which has a 1 for each letter set in the die. That would speed things up. However, I'm not doing it for lack of time. Maybe next semester. That said, your program should not run more slowly than mine.
The first step -- reading the input and creating the graphs
The program readorig was my first step -- reading the input, creating the network flow graph, and printing it out. Note, my program does not have duplicate edges.UNIX> readorig Dice1.txt Words1.txt Node 0: SOURCE Edges to 1 2 3 4 Node 1: ENG Edges to 7 8 Node 2: SAA Edges to 6 Node 3: PRR Edges to 5 Node 4: EAE Edges to 6 8 Node 5: R Edges to 9 Node 6: A Edges to 9 Node 7: G Edges to 9 Node 8: E Edges to 9 Node 9: SINK Edges to Node 0: SOURCE Edges to 1 2 3 4 Node 1: ENG Edges to 6 7 Node 2: SAA Edges to 5 Node 3: PRR Edges to 8 Node 4: EAE Edges to 6 7 Node 5: S Edges to 9 Node 6: E Edges to 9 Node 7: E Edges to 9 Node 8: P Edges to 9 Node 9: SINK Edges to Node 0: SOURCE Edges to 1 2 3 4 Node 1: ENG Edges to 5 Node 2: SAA Edges to Node 3: PRR Edges to 6 7 Node 4: EAE Edges to 5 Node 5: E Edges to 8 Node 6: R Edges to 8 Node 7: R Edges to 8 Node 8: SINK Edges to Node 0: SOURCE Edges to 1 2 3 4 Node 1: ENG Edges to 6 7 8 Node 2: SAA Edges to Node 3: PRR Edges to 5 Node 4: EAE Edges to 6 7 Node 5: P Edges to 9 Node 6: E Edges to 9 Node 7: E Edges to 9 Node 8: N Edges to 9 Node 9: SINK Edges to Node 0: SOURCE Edges to 1 2 3 4 Node 1: ENG Edges to 5 Node 2: SAA Edges to 6 7 Node 3: PRR Edges to 8 Node 4: EAE Edges to 6 Node 5: G Edges to 9 Node 6: A Edges to 9 Node 7: S Edges to 9 Node 8: P Edges to 9 Node 9: SINK Edges to UNIX>
Examples
I have a few example files besides the above:Dice2.txt and Words2.txt are small files to test variable-sized dice:
UNIX> cat Dice2.txt E PITED FOGCEF UNIX> cat Words2.txt DOG PIG CAT DO TEE FEE UNIX> worddice Dice2.txt Words2.txt Cannot spell DOG Cannot spell PIG Cannot spell CAT 1,2: DO 1,0,2: TEE 2,0,1: FEE UNIX>
Dice3.txt is a file with six randomly generated six-sided dice, and Words3.txt contains all words from the Unix dictionary that have six letters.
UNIX> cat Dice3.txt IBTLCP DUAQEM DXLOTN WMIVQA NDCLOT JKCEMR UNIX> head Words3.txt AARHUS ABACUS ABATER ABBOTT ABDUCT ABJECT ABLATE ABLAZE ABOARD ABOUND UNIX> worddice Dice3.txt Words3.txt | head Cannot spell AARHUS Cannot spell ABACUS Cannot spell ABATER Cannot spell ABBOTT 3,0,2,1,5,4: ABDUCT 3,0,5,1,4,2: ABJECT 1,0,2,3,4,5: ABLATE Cannot spell ABLAZE 1,0,2,3,5,4: ABOARD Cannot spell ABOUND UNIX>
Dice4.txt is a file with eight randomly generated dice with between three and seven sides. Words4.txt contains all words from the Unix dictionary that have eight letters. As worddice shows, there are fewer successful spellings in this example:
UNIX> cat Dice4.txt FJZ BSYQ WYUTI SHTXVU PRAFYBH LWQCEI ENLJB BTJO UNIX> head Words4.txt ABDICATE ABERDEEN ABERRANT ABERRATE ABETTING ABEYANCE ABHORRED ABLUTION ABNORMAL ABORNING UNIX> worddice Dice4.txt Words4.txt | head Cannot spell ABDICATE Cannot spell ABERDEEN Cannot spell ABERRANT Cannot spell ABERRATE Cannot spell ABETTING Cannot spell ABEYANCE Cannot spell ABHORRED Cannot spell ABLUTION Cannot spell ABNORMAL Cannot spell ABORNING UNIX> worddice Dice4.txt Words4.txt | grep ':' | head 7,6,4,2,3,5,0,1: BEAUTIFY 1,6,7,2,0,5,3,4: BLOWFISH 7,5,3,6,0,2,1,4: BLUEFISH 6,7,4,1,2,0,3,5: BOASTFUL 5,0,4,3,1,2,7,6: EFFUSION 0,4,6,2,5,7,3,1: FABULOUS 0,6,4,7,5,2,3,1: FEROCITY 0,5,1,7,2,3,4,6: FESTIVAL 0,2,6,4,7,3,5,1: FIBROSIS 0,6,4,2,3,5,1,7: FLAUTIST UNIX>
Dice5.txt is a file with twenty randomly generated 5-sided dice and Words5.txt contains all words from the Unix dictionary:
UNIX> wc Dice5.txt
20 20 120 Dice5.txt
UNIX> head -n 5 Dice5.txt
CWOZP
YFLBV
VNJGT
PUISB
MCGNQ
UNIX> wc Words5.txt
24854 24853 205394 Words5.txt
UNIX> head -n 5 Words5.txt
AAA
AAAS
AARHUS
AARON
AAU
UNIX> time worddice Dice5.txt Words5.txt > /dev/null
20.827u 0.100s 0:21.07 99.2% 0+0k 0+0io 0pf+0w
UNIX>
It takes a little time, doesn't it? (These timings are from 2008: This is on my MacBook Pro with a 2.16 Ghz processor.
The Linux box in my office (much older) takes roughly twice as long. The cetus lab
machines take 32 seconds).
Let's see if using compiler optimization helps:
UNIX> g++ -O -o worddice worddice.cpp UNIX> time worddice Dice5.txt Words5.txt > /dev/null 2.736u 0.050s 0:02.80 99.2% 0+0k 0+1io 0pf+0w UNIX>Wow. The optimized version is in the lab directory and takes 2.85 seconds on the cetus machines.
We can use our mastery of Unix tools like sed, awk and grep to answer some questions. For example, how many words can be spelled, and how many cannot:
UNIX> worddice Dice5.txt Words5.txt | grep ':' | wc
24400 48800 623204
UNIX> worddice Dice5.txt Words5.txt | grep Cannot | wc
453 1359 10819
UNIX>
Quite a high success ratio -- 24400/24953 = 97.8 percent. What's the largest
word that you can spell:
UNIX> worddice Dice5.txt Words5.txt | grep ':' | sed 's/,/ /g' | awk '{ print NF }' | sort -u
10
11
12
13
14
15
16
17
18
19
4
5
6
7
8
9
UNIX> worddice Dice5.txt Words5.txt | grep ':' | sed 's/,/ /g' | awk '{ if (NF == 19) print $NF }'
DIETHYLSTILBESTROL
ELECTROCARDIOGRAPH
UNIX>
What's the smallest word that you can't spell:
UNIX> worddice Dice5.txt Words5.txt | grep Cannot | awk '{ print $NF }' | sed 's/./x/g' | sort -u
xxx
xxxx
xxxxx
xxxxxx
xxxxxxx
xxxxxxxx
xxxxxxxxx
xxxxxxxxxx
xxxxxxxxxxx
xxxxxxxxxxxx
xxxxxxxxxxxxx
xxxxxxxxxxxxxx
xxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxx
UNIX> worddice Dice5.txt Words5.txt | grep Cannot | awk '{ print $NF }' | grep '^...$'
AAA
UNIX>