 |
I'm going to give you the descriptions of the programs first, and then after all the descriptions, I'll give hints on how to turn the problem into a solution.
As an extra twist, Maui says that after each roll, he can offer them a certain amount of prize money for them to quit. Perhaps each roll will be represented by a model wearing glittery clothes. He hasn't figured out those details yet. Regardless, he would like to be able to know the probability of success at each phase of the game so that he may set odds. That's where you come in.
Maui wants you to write a program called dond.cpp that will be called with three parameters:
UNIX> dond s t last-roll |
If last-roll is -1, then the program should print the probability of a contestant rolling an s-sided die t times succesfully. Otherwise, it should assume that the contestant has last rolled the value in last-roll, and we now want the probability of rolling the die t more times successfully.
Your program's output should match mine, which does error-check the command line parameters. The solution is a straightforward dynamic program with memoization if you want to structure it that way. You can also ditch the recursion and make it a straightforward iterative program. My solution was dynamic, because it required less thinking.
I won't give any hints or help here -- if you want some help, read the help at the end of this file.
For the grading, your program's output needs to match mine exactly on legal input.
 |
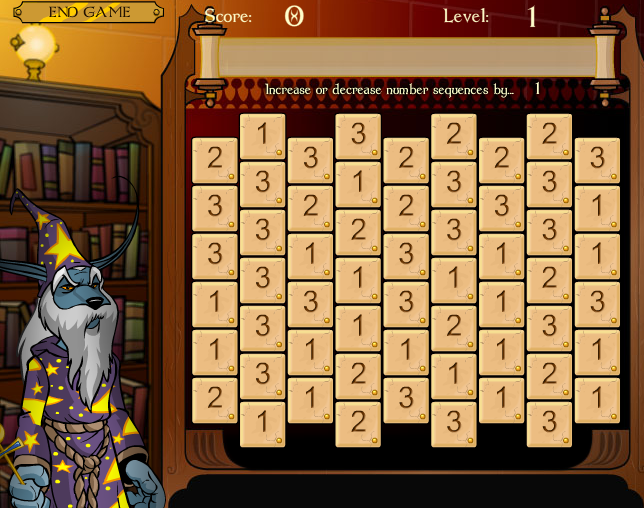
Your job is to score points by discovering long paths in the game board, where a path consists of adjacent squares whose numbers differ by one. So, for example, the following board shows a path of seven squares.
 |
In the Neopets game, that dog wizard tells you that your path is ok. In our lab, there is no dog wizard. Sorry.
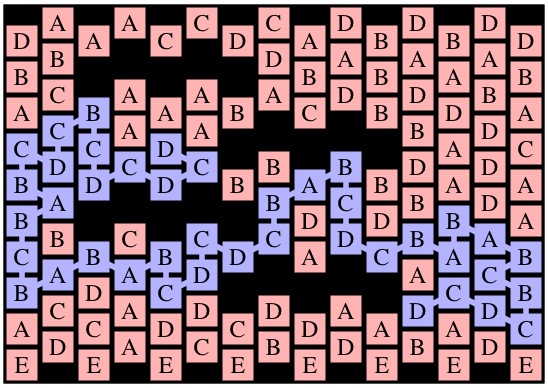
In the lab, we will define a grid with an input file, like example.txt, which represents the grid above:
213322223 332123331 331231121 133131123 131211121 231231121 -1-2-3-3- |
The format of the input file is words, where each word must contain the same number of letters. The first word contains the top "row" of the grid; however the rows are skewed so that even columns are a half a square lower than odd columns (zero-indexing, of course). You may specify that a cell is empty with a hyphen.
All rows must have the same number of cells. Any cell may be blank. Cells are not restricted to have numbers -- letters are fine too, although we use ASCII values to determine whether two cells may be in a path together.
I have some example input files in the lab directory, plus a program spellgen that generates random input files, and a program spellscreen that converts an input file into a jgraph file so that you can look at it (pipe the output through jgraph -P to get a Postscript picture). Spellscreen also does error checking for correctness. Your program does not have to do so.
Some example inputs are below:
easy-ones.txt
1111 1111 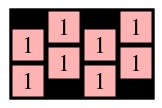 |
easy-3x4.txt
ABBB BBAB -B-A 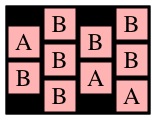 |
example.txt
213322223 332123331 331231121 133131123 131211121 231231121 -1-2-3-3- 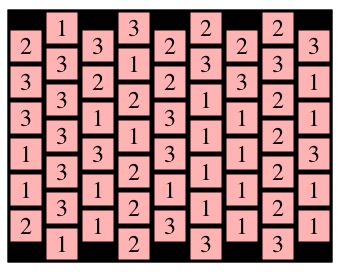 |
10x15.txt
DAAACCDCADBDBDD BB-----DBABAAAB ACBAAABACDBDDBA CCCADA-----BADC BDDCDCBBABBDADA BA-----BDCDBBDA CBBCBCDCADCBAAB BADACD-----ACCB ACCADDCDDAADADC EDEAECEBEDEBEDE  |
04x27.txt
yxxxzzyzxywywyywwxzxywywxwx xxwxzwxxxwxzywyywxzzzxyxxzz ywwxyzwyyzyzwwxwwyxyxwxxzwy zzywxywzyyxwxwxyzxyzxwxwyzx  |
We will index cells by (row,column), where row zero is at the top and column zero is at the left. Thus, the cell at (0,0) in 10x15.txt is D, the cell (0,1) is A and the cell at (1,0) is B.
Formally, two cells are adjacent if:
 0 0 |
 0 1 0 0 1 1 1 2 1 3 2 3 |
 4 6 5 7 4 8 4 7 3 6 3 7 2 6 2 7 1 6 0 6 1 5 0 4 1 3 1 2 2 2 2 3 3 3 4 3 4 2 5 3 5 2 6 3 5 4 |
 3 4 4 5 4 4 4 3 4 2 3 2 2 2 3 1 4 1 3 0 4 0 5 1 5 0 6 0 7 0 7 1 6 2 7 3 6 4 7 4 7 5 6 5 6 6 6 7 5 7 4 8 4 9 5 9 6 9 6 10 6 11 6 12 5 12 6 13 6 14 7 13 7 14 8 14 8 13 7 12 8 11 |
 0 17 0 16 1 17 2 17 3 17 3 18 2 18 2 19 1 19 0 20 1 21 2 21 2 20 3 21 2 22 3 23 2 23 1 22 1 23 0 23 0 24 0 25 0 26 |
You are to write two programs. The first is easier than the second. The first is called spellpath. It should read a grid on standard input and print out the length of the longest path through the grid:
UNIX> spellpath < easy-ones.txt 1 UNIX> spellpath < easy-3x4.txt 6 UNIX> spellpath < example.txt 23 UNIX> spellpath < 10x15.txt 41 UNIX> spellpath < 04x27.txt 23 UNIX>Spellpath should be a dynamic program, which does not have to use memoization. This means that it doesn't have to be too fast. If you want help, see below.
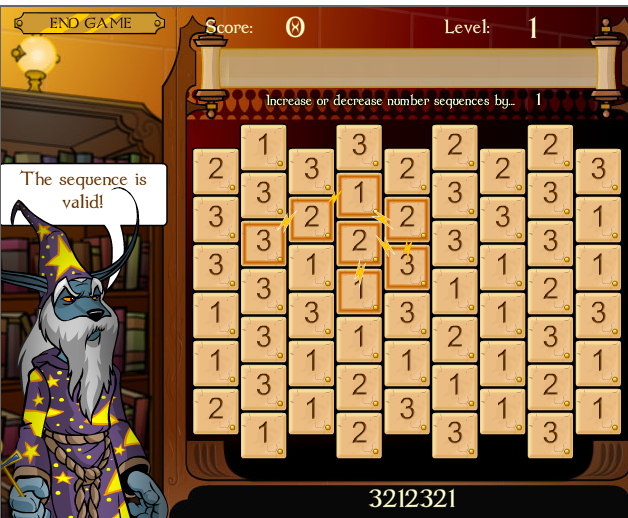
The second program, called spellseeker needs to output the path. It should do so by first outputting the grid, then the word "PATH", and then the path itself. Your output does not have to match mine, but the path must be a legal longest path. You can check for validity with the program spellchecker. So, for example:
UNIX> spellseeker < easy-ones.txt 1111 1111 PATH 0 0 UNIX> spellseeker < easy-3x4.txt ABBB BBAB -B-A PATH 0 1 0 0 1 1 1 2 1 3 2 3 UNIX> spellseeker < easy-3x4.txt | spellchecker OK - Pathlength = 6 UNIX>Spellseeker should be a dynamic program that uses memoization to make it fast. The gradescript will test for speed, and if your program takes more than a second longer than mine, it will kill your program and count it as wrong. As with spellpath, if you want some help, read the help below.
UNIX> dond 6 1 -1 1 UNIX> dond 6 1 0 0.666667 UNIX> dond 6 1 1 0.5 UNIX> dond 6 1 2 0.5 UNIX> dond 6 1 3 0.5 UNIX> dond 6 1 4 0.5 UNIX> dond 6 1 5 0.666667 UNIX>So, consider t=2 and last-roll=-1. This will be the sum of times that t=1 and lastroll ≠ -1, divided by six. Put another way, you have a 1/6 probability of rolling a zero. If you roll a zero, you have a 2/3 chance of winning. Ditto when you roll a five. If you roll a 1 through 4, you have a 1/2 chance of winning. So, your probability of winning when t=2 is 1/6 * (2/3 + 2/3 + 1/2 + 1/2 + 1/2 + 1/2). That value is 0.555556:
UNIX> dond 6 2 -1 0.555556 UNIX>Now consider t=2 and last-roll=0. Well, 1/6 of the time, you will roll a zero on your next roll, and 1/6 of the time, you will roll a one. In each of those, you lose. However, 1/6 of the time, you will roll a 2, and your chance of winning will be "dond 6 1 2", which is 1/2. The same is true when you roll a 3 or a 4. 1/6 of the time, you'll roll a 5, and your chance of winning will be 2/3. Therefore, if t=2 and last-roll=0, your chance of winning will be 1/6*(0 + 0 + 1/2 + 1/2 + 1/2 + 2/3). That value is 0.361111:
UNIX> dond 6 2 0 0.361111 UNIX>You should be able to confirm all of the calls below by hand. For example, dond 6 2 1 will equal 1/6*(0 + 0 + 0 + 1/2 + 1/2 + 2/3), and dond 6 2 2 will equal 1/6*(2/3 + 0 + 0 + 0/2 + 1/2 + 2/3).
UNIX> dond 6 2 1 0.277778 UNIX> dond 6 2 2 0.305556 UNIX> dond 6 2 3 0.305556 UNIX> dond 6 2 4 0.277778 UNIX> dond 6 2 5 0.361111 UNIX>The recursion should be getting clearer. dond 6 3 -1 will equal 1/6*(0.361111 + 0.277778 + 0.305556 + 0.305556 + 0.277778 + 0.361111) = 0.314815:
UNIX> dond 6 3 -1 0.314815 UNIX>
Can you spot how to write MaxPathLen() recursively? I'll tell you below.
Let n be the cell at (row, col). Let (r,c) be a cell adjacent to n whose value is exactly one less than or one greater than n's value. Then call MaxPathLen(r, c, grid-n), where grid-n is the grid with cell n removed. Do this for all (r,c). The return value for MaxPathLen(row, col, grid) will be one plus the maximum MaxPathLen(r, c, grid-n) for all the (r,c).
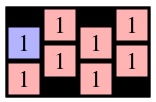
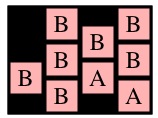
Here's an example that uses the following three pictures:
 |
 |
 |
| g1 | g2 | g3 |
Consider those three recursive calls. The first two will return instantly with max path lengths of one, because cells (0,1) and (1,0) in g2 are only adjacent to B's. The call to MaxPathLen(1,1,g2), however, will make a recursive call to MaxPathLen(1,2,g3).
You should see how it goes now -- that call will eventually return 3, which means that MaxPathLen(1,1,g2) will return 4. Since that is the maximum of the three recursive calls on g2, MaxPathLen(0,0,g1) will return 5.
If you call MaxPathLen on every cell of the original grid, the one with the maximum value will be the maximum length path.
You can hack this up fairly easily. When you call MaxPathLen(row, col, grid), save the value of (row, col) in a temporary variable and set the value to '-'. Make all of the recursive calls, and then set the value back to the saved value before you return to the caller. Spellpath called on all of the examples above should take well less than a second to run.
class Answer {
public:
int length;
int r;
int c;
string key;
Answer *nexta;
};
|
I also have a Spellseeker class that contains my grid, the memoization cache, the total rows and columns and a Solve() method:
class SpellSeeker {
public:
vector <string> grid;
map <string, Answer *> cache;
int total_r;
int total_c;
Answer *Solve(int r, int c);
};
|
As you can see, Solve(r, c) returns an (Answer *). The r and c fields contain the r and c values of the Solve() call. Length is the maximum length path, and nexta contains the (Answer *) of the next node in the path. If there is no next node, nexta is NULL. Key is a string that represents the grid. It is the key for my memoization cache.
When I call Solve(), I first calculate a key from the grid, then look up the key in my cache. If it's there, then I return its contents (which is an (Answer *)). If it's not there, then I create a new (Answer *) and set its r, c and key fields. I then make recursive calls as in spellpath above, only the recursive calls return (Answer *)'s instead of lengths. As with spellpath, I modify the grid before making the recursive calls (taking the element in (r,c) out of the grid, and when I'm done with them, I put the element back. I take the best of the recursive calls, and use it as my nexta field. I set the length equal to one plus the length of the nexta field, put the (Answer *) into the memoization cache and return it.
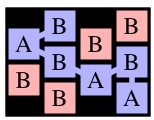
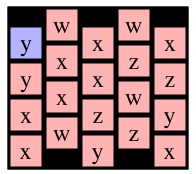
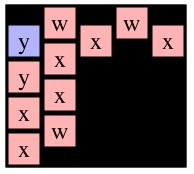
Now, to create the key, you should notice that when you call Solve(r,c), the only nodes that matter are the ones reachable from cell (r, c). What I do is create a key that identifies those nodes and node (r,c) as the starting node. To help illustrate this, let's consider a call to Solve(0,0) on g4 below (I've colored node (0,0) blue).
 |
 |
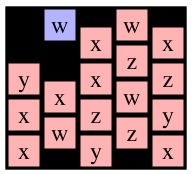 |
| g4 | g5 | g6 |
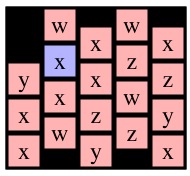
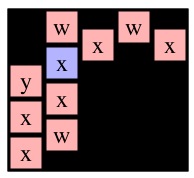
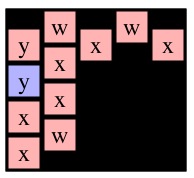
Now, instead, consider a call to Solve(1,0) on g4. I've drawn it with cell (1,0) blue below:
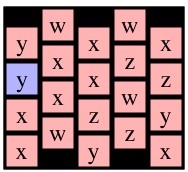 |
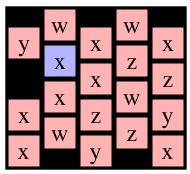 |
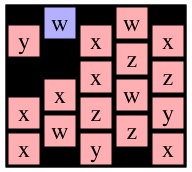 |
| g4 | g7 | g8 |
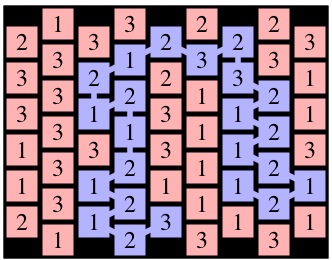
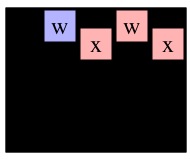
Now think about the two recursive calls to Solve(0,1). Even though graphs g6 and g8 differ, the two Solve(0,1) calls are exactly the same and will return the same path. This piece of insight helps our memoization. The first thing that we do when we make a call to Solve(r,c) is perform a DFS on the given cell to identify all the nodes reachable from (r,c). We show these DFS results for each of the six example calls to Solve() above:
 |
 |
 |
 |
 |
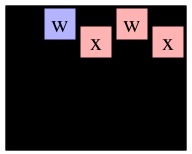 |
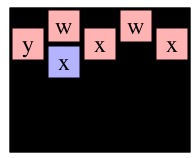
| Solve(0,0) on g4 | Solve(1,1) on g5 | Solve(0,1) on g6 | Solve(1,0) on g4 | Solve(1,1) on g7 | Solve(0,1) on g8 |
See how the two calls to Solve(0,1) are exactly alike. After performing the DFS, I turn it into a key, and that is the lookup key in my memoization cache. The way I construct my key is as follows: I create a string that has an entry for each cell in the grid (empty or not). I set all the entries to '-'. I then set the entry for (r,c) to 'X'. Then I call the depth-first search routine that marks all nodes reachable from node (r,c), and sets their entries to 'O'. When I'm done, I have constructed my key. For example, the key for Solve(0,1) on g6 and g8 is: "-XOOO---------------". The key for Solve(1,1) on g7 is "OOOOO-X-------------". The key for Solve(0,0) on g4 is "XOOOOOO---OO---OO---".
The memoization helps drastically in performance. For example, calling spellseeker on 20x20.txt takes about four tenths of a second on my Mac (this is when g++ is called with -O2). Without memoization, it takes so long that I gave up and killed it before it terminated.
