 |
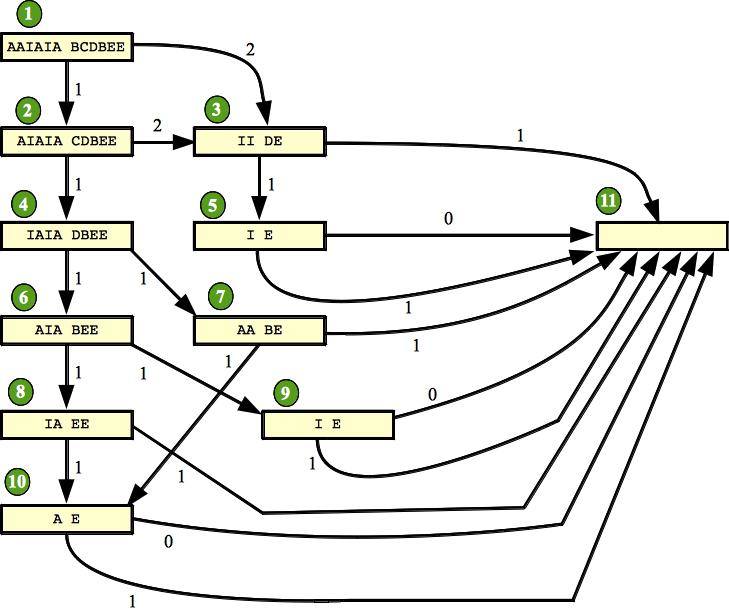
For example, consider the following graph (from the Topcoder problem ConvertibleStrings, which we use as an example of Dynamic progrmaming). The numbers in green show a valid topological sort of the graph:
 |
As I said before, the sortings do not have to be unique. For example, you could swap the 3rd and 4th nodes in the sort, and you would still have a valid sort.
To perform a topological sort, you maintain a list of nodes with no incoming edges. Then, until that list is empty, you do the following:
This is guaranteed to work, because the graph is acyclic. The running time is O(|V|+|E|). Like DFS and BFS, it visits each node once, and each edge once.
There are some problems that you can solve with topological sort:
Is that better than Dijkstra's algorithm? Yes and no. See the analysis below.
What I've done is write two programs: src/topo.cpp and src/dijkstra.cpp (I don't let you see dijkstra.cpp -- for myself, see my personal 302 page for how to get dijkstra.cpp).
These take the following command line arguments:
topo|dijkstra n maxcap mincap window seed print(y|n) |
The programs create random directed, acyclic graphs with n nodes, numbered 0 through n-1. The edges all have random capacities uniformly distributed between mincap and maxcap.
The structure of the graph depends on window:
UNIX> bin/topo 4 50 1 2 1 y Node 0: [1,35][2,44] Node 1: [2,26][3,6] Node 2: [3,48] Node 3: Total edges in graph: 5 Shortest Path: 41 Edges Processed: 5 Graph Creation Time: 0.000 Shortest Path Time: 0.000 UNIX> bin/dijkstra 4 50 1 2 1 n Total edges in graph: 5 Shortest Path: 41 Edges Processed: 4 Graph Creation Time: 0.000 Shortest Path Time: 0.000 UNIX> |
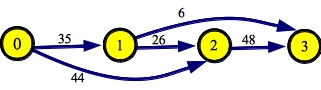 |
It's pretty easy to see that the shortest path is 0 -> 1 -> 3. And you can see the difference between topological sort and Dijkstra -- topological sort has to process every edge. Dijkstra on the other hand, does not visit node 2, because the shortest path to node 3 is shorter than the one to node 2. For that reason, the edge from 2 to 3 is not processed.
Let's look at a larger example to see a class of graphs where Dijkstra's algorithm will outperform topological sort: Those where window equals n. Here's an example where n equals 8:
UNIX> bin/topo 8 10 1 8 8 y Node 0: [1,7][2,7][3,1][4,10][5,3][6,9][7,4] Node 1: [2,7][3,5][4,3][5,3][6,2][7,6] Node 2: [3,5][4,7][5,1][6,2][7,4] Node 3: [4,3][5,6][6,1][7,2] Node 4: [5,4][6,6][7,5] Node 5: [6,8][7,3] Node 6: [7,1] Node 7: Total edges in graph: 28 Shortest Path: 3 Edges Processed: 28 Graph Creation Time: 0.000 Shortest Path Time: 0.000 UNIX> bin/dijkstra 8 10 1 8 8 n Total edges in graph: 28 Shortest Path: 3 Edges Processed: 14 Graph Creation Time: 0.000 Shortest Path Time: 0.000 UNIX>To help visualize this, I'm drawing the graph below, where the edges are colored according to their weights:
 |
What you can see here is that while topological sort has to process all 28 edges, Dijkstra's algorithm only processes the edges from nodes 0, 3 and 6. Let's extrapolate and time. In each of these tests, maxcap is 1000, mincap is one, window is equal to n.
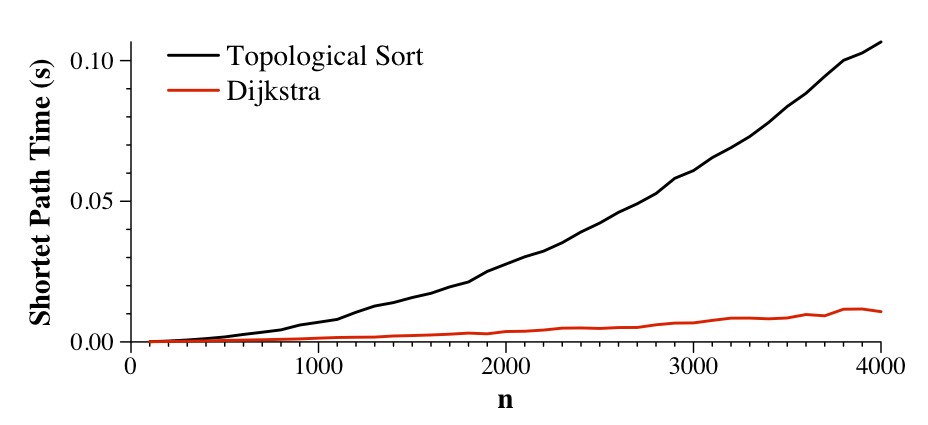 |
I'm not super-proud of that graph, BTW -- the Dijkstra numbers are averages of 50 runs each, but there's still so enough randomness in the graphs that you see wavy lines. However, what you are seeing is that Dijkstra's algorithm processes so many fewer edges than topological sort, that it is over ten times faster on the larger graphs.
Now, let's instead construct graphs that favor topological sort. Let's make n big, but limit window to 64. Here's an example:
UNIX> bin/topo 10000 1000 1 64 1 n Total edges in graph: 637920 Shortest Path: 2102 Edges Processed: 637920 Graph Creation Time: 0.048 Shortest Path Time: 0.010 UNIX> bin/dijkstra 10000 1000 1 64 1 n Total edges in graph: 637920 Shortest Path: 2102 Edges Processed: 635321 Graph Creation Time: 0.053 Shortest Path Time: 0.015 UNIX>Now, you can see that Dijkstra's algorithm is processing nearly all of the edges on the graph. Since it has to do map operations, which are O(log m) (where m is the size of the map), it is slower than topological sort, which is doing O(1) operations for each edge.
Let's look at how the timings scale with n when we keep window fixed at 64:
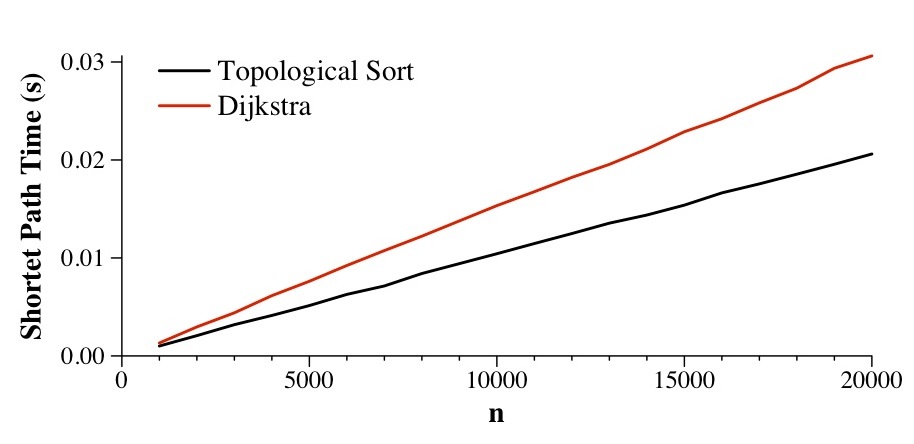 |
It's no longer a 10-fold improvement, but the topological sort clearly outperforms Dijkstra.
These are nice examples of showing how the structure of the graph impacts the performance of the two algorithms.
 |
If we set -w constant at -500, and increase n up to 50,000, and set the weights from 1 to 1000, you'll see that Topological Sort outperforms Dijkstra more dramatically:
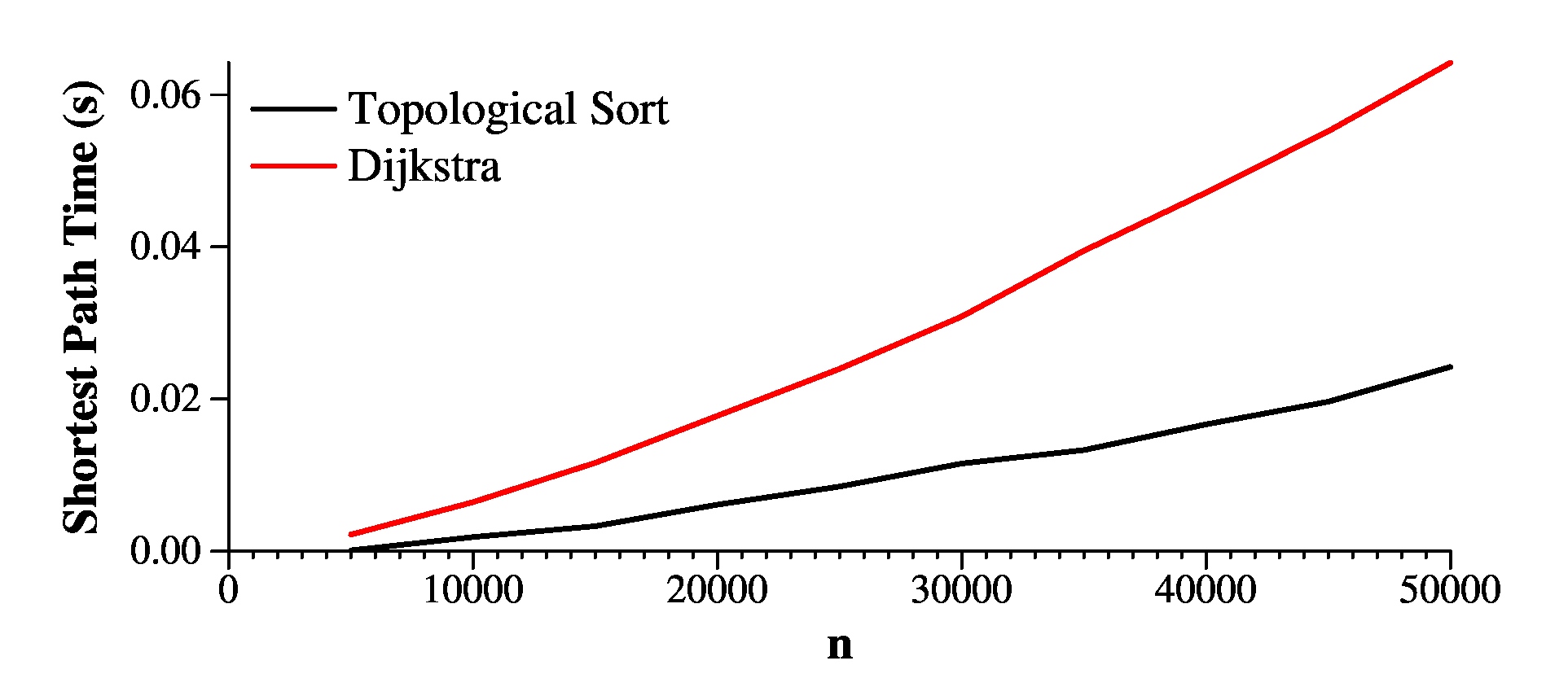 |
Again, this is because both Dijkstra and topological sort process similar numbers of edges:
UNIX> bin/topo 50000 1000 1 -500 1 n Total edges in graph: 4990098 Shortest Path: 2421 Edges Processed: 4990098 Graph Creation Time: 0.105 Shortest Path Time: 0.018 UNIX> bin/dijkstra 50000 1000 1 -500 1 n Total edges in graph: 4990098 Shortest Path: 2421 Edges Processed: 4976077 Graph Creation Time: 0.106 Shortest Path Time: 0.046 UNIX>If we reduce the number of layers to five, Dijkstra's algorithm vastly outperforms Topological Sort, because as you can see, the shortest path is 7, and Dijkstra processes the final node off the multimap quickly, and doesn't process nearly as many edges:
UNIX> bin/topo 10000 1000 1 -5 1 n Total edges in graph: 16001998 Shortest Path: 7 Edges Processed: 16001998 Graph Creation Time: 0.164 Shortest Path Time: 0.046 UNIX> bin/dijkstra 10000 1000 1 -5 1 n Total edges in graph: 16001998 Shortest Path: 7 Edges Processed: 870000 Graph Creation Time: 0.160 Shortest Path Time: 0.010 UNIX>Let me illustrate this effect with a few pictures. Here's Dijkstra's algorithm on a run where n = 102 and w = -5. I've colored the edges that are processed by the algorithm in red (you can click on the drawing to blow it up):
 |
You'll notice that there are only 2 of 20 nodes in the first layer that get processed. There are only six in the second layer, 8 in the third layer, and 13 in the fourth layer. Each node that doesn't get processed is responsible for 20 edges, so as you can see, Dijkstra's algorithm avoids processing a lot of edges.
I'm repeating myself here, but a node only gets processed if its shortest distance to the starting node is less than the ending node's shortest distance. Since the edge weights are randomly chosen from [1,1000], there are a lot of nodes that do not get processed.
Now, take a look at what happens we double the size of this graph. We'll have 202 nodes and 10 layers. In this way, each layer has 20 nodes, but we've doubled the number of layers and nodes:
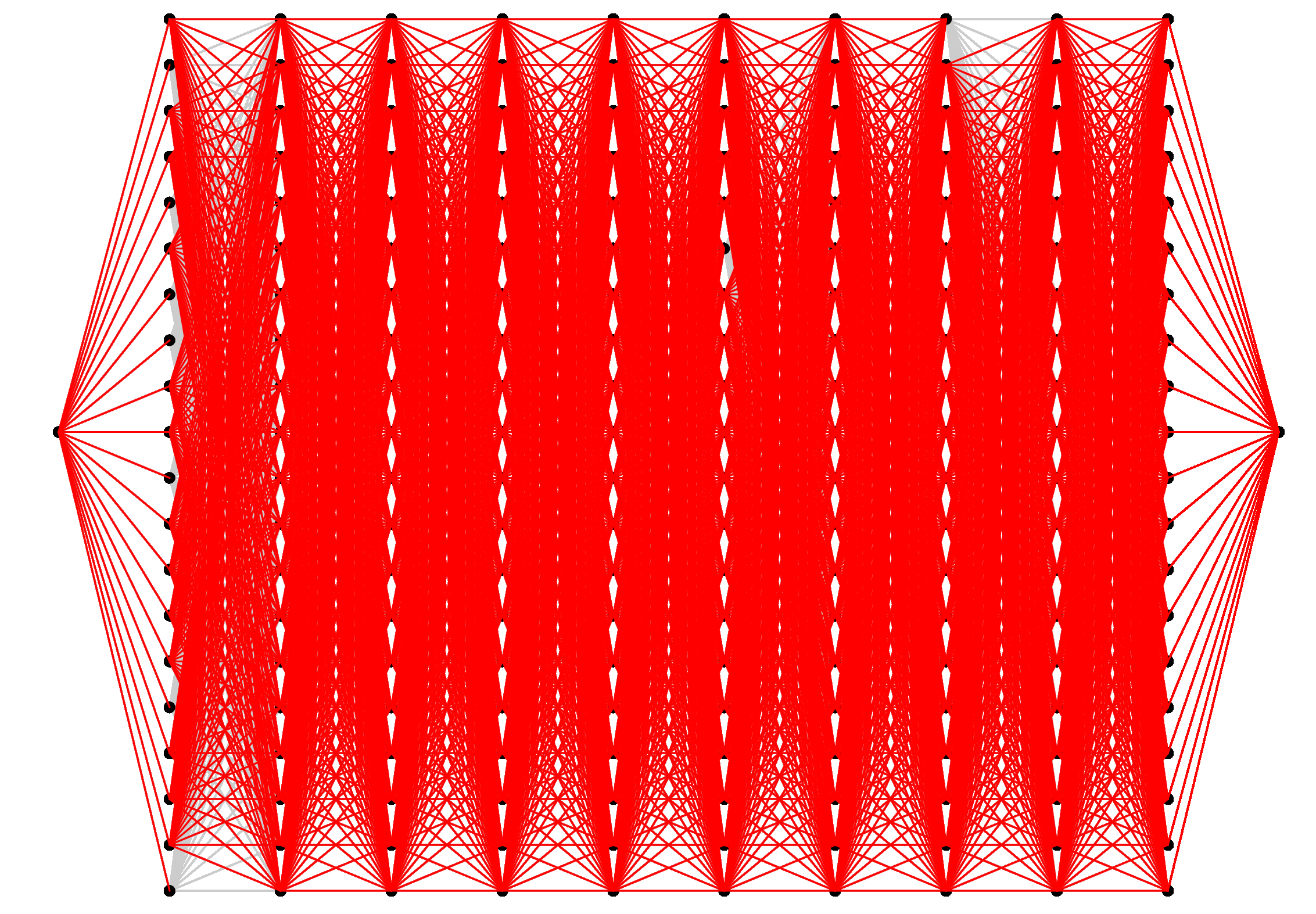 |
Now, as you can see, there are only 9 nodes of the 202 that do not get processed. This is why Topological Sort works better on this graph than Dijkstra's algorithm.
Suppose I want to force Dijkstra's algorithm to process every edge. One way to do this is to add another node and edge -- the edge goes to this node, and comes from the last node in the graph. I give the edge a weight of 5000, which means that the shortest path to it is greater than every other node in the graph. Therefore, Dijkstra's algorithm has to process every node and edge.
When we time it, the gap between topological sort and Dijkstra's algorithm narrows, but topological sort is still slower. That is a curiosity to me. I wouldn't think that it would be the case:
UNIX> bin/topo 10000 1000 1 -5e 1 n # (The "e" makes the extra node and edge) */ Total edges in graph: 16001999 Shortest Path: 5007 Edges Processed: 16001999 Graph Creation Time: 0.272 Shortest Path Time: 0.058 UNIX> bin/dijkstra 10000 1000 1 -5e 1 n Total edges in graph: 16001999 Shortest Path: 5007 Edges Processed: 16001999 Graph Creation Time: 0.272 Shortest Path Time: 0.051 UNIX>Why is Dijkstra's algorithm still faster, even though both algorithms are processing all of the edges? I'm going to guess the following -- the main loop of Dijkstra's algorithm is something like the following:
- Remove a node f from the multimap
- Visit each of f's edges
- For each edge (f,t)
- If the distance to t is shorter going through f, then:
- Delete t from the multimap if it's there.
- Reinsert t into the multimap keyed on its new distance
This is where O(E log V) comes from. Let's suppose that the "If" statement is false
most of the time. Then those log operations are rarely performed. I'm guessing that this
is what's happening. I really should instrument the code so that we can confirm this hypothesis,
but I'm getting tired of fiddling with this lecture...
I also believe that the topological sort code can be sped up by getting rid of the deque, adding a vector of links to the graph (one for each node), then then implementing a stack instead of a queue. This is in src/topo2.cpp, which I haven't taken the time to comment, but it is significantly faster than src/topo.cpp:
UNIX> bin/topo2 10000 1000 1 -5e 1 n Total edges in graph: 16001999 Shortest Path: 5007 Edges Processed: 16001999 Graph Creation Time: 0.287 Shortest Path Time: 0.041 UNIX>That's enough of a rabbit hole....