 |
 |
 |
 |
 |
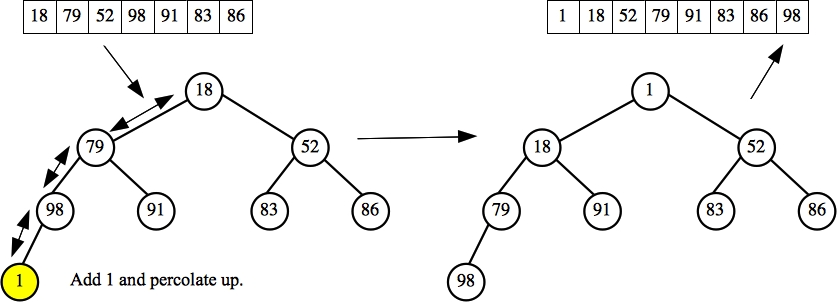 |
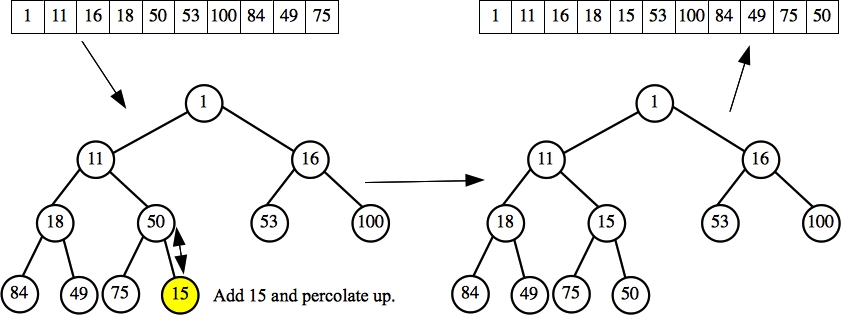 |
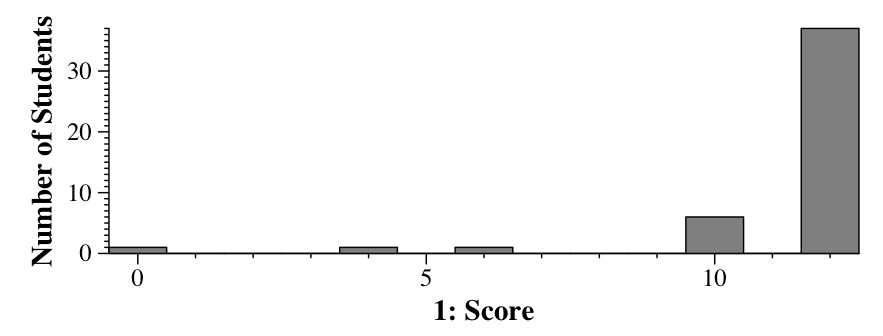 |
Elts: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 Links: 4 -1 -1 11 -1 11 4 4 12 -1 11 -1 4 -1 4 11 1 20 10 13 -1 4 13 13 Ranks: 1 2 1 1 3 1 1 1 1 1 2 3 2 2 1 1 1 1 1 1 2 1 1 1 Union(20,4) = 4 Find(17) = 4 Find(18) = 11 Elts: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 Links: 4 Ranks: |
2B: Since 7's size is greater than 22's, it will be the parent, so Union(7,22), returns 7. Links[22] will become 7 and Ranks[7] will become 8. The two Find() commands return 10 and 7 respectively.
Elts: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 Links: 21 21 7 -1 10 3 15 -1 21 21 -1 4 7 7 10 10 22 -1 2 3 -1 -1 -1 22 Ranks: 1 1 2 3 2 1 1 5 1 1 6 1 1 1 1 2 1 1 1 1 1 5 3 1 Union(7,22) = 7 Find(11) = 10 Find(23) = 7 Elts: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 Links: 7 Ranks: 8 |
2C: Now 7's rank is greater than 14's, so it becomes 14's parent. That changes links[14] to 7. The Find(10) command will now return 7, and because of path compression, links[10] is set to 7. Find(16) returns 19, and again because of path compression, links[16] is set to 19:
Elts: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 Links: 19 7 21 20 19 7 9 -1 5 -1 14 17 1 21 -1 7 0 -1 7 -1 7 -1 17 -1 Ranks: 2 2 1 1 1 2 1 3 1 2 1 1 1 1 2 1 1 2 1 3 2 2 1 1 Union(14,7) = 7 Find(10) = 7 Find(16) = 19 Elts: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 Links: 7 7 19 Ranks: |
2D: For the last one, the two sets have the same rank, so the tie is broken in favor of the higher set id: 22. Ranks[22] is incremented, because Union by Rank works like Union by Height, even though the ranks do not strictly represent heights. The Unions() operations also sets links[14] to 22. Find(13) now returns 22, and because of path compression, links[13] and links[20] are both set to 22. Find(1) also returns 22 and sets links[1] to 22.
Elts: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 Links: 22 0 15 5 22 -1 14 15 -1 8 11 -1 16 20 -1 -1 5 7 0 -1 14 7 -1 22 Ranks: 2 1 1 1 1 3 1 2 2 1 1 2 1 1 3 3 2 1 1 1 2 1 3 1 Union(14,22) = 22 Find(13) = 22 Find(1) = 22 Elts: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 Links: 22 22 22 22 Ranks: 4 |
On part D, if you made 14 the parent instead of 22, I took two points off by giving you zero for the unions and finds. However, if you made the links equal 14, and 14's rank equal 4, you still got full credit for that part.
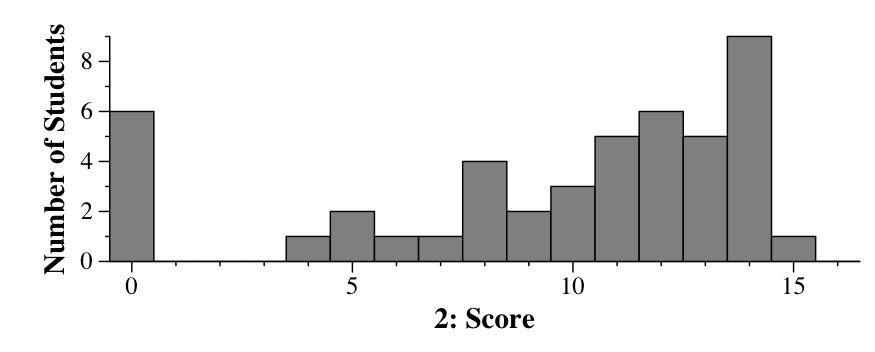 |
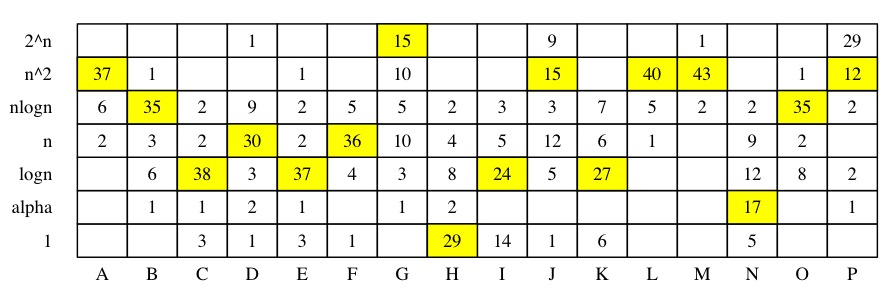
| A: Sorting a vector using insertion sort. | O(n2) |
| B: Sorting a vector using heap sort. | O(n log n) |
| C: Calling Push() on a heap. | O(log n) |
| D: Creating a heap from a random vector. | O(n) |
| E: Calling Pop() on a heap. | O(log n) |
| F: Printing all elements of a map in order. | O(n) |
| G: Printing all subsets of a set. | O(2n) |
| H: Calling Union() on a disjoint set. | O(1) |
| I: Deleting an element from a map. | O(log n) |
| J: Printing all pairs of elements in a vector of integers. | O(n2) |
| K: Inserting an element into a map. | O(log n) |
| L: Sorting a vector using selection sort. | O(n2) |
| M: Sorting a vector using bubble sort. | O(n2) |
| N: Calling Find() on a disjoint set. | O(α(n)) |
| O: Sorting a vector using STL multisets. | O(n log n) |
| P: Enumerating all 2-disk failures in an n-disk system. | O(n2) |
Each question is worth a point.
 |
 |
 |
#include <string>
#include <iostream>
using namespace std;
main()
{
int i, j, k;
string s;
s.resize(10, ' ');
for (i = 0; i < (1 << 9) ; i++) {
for (j = 0; j < 9; j++) {
if (i & (1 << j)) {
s[j] = 'A';
} else {
s[j] = 'B';
}
}
for (j = 0; j < 10; j++) {
for (k = 0; k < j; k++) cout << s[k];
cout << 'C';
for (; k < 9; k++) cout << s[k];
cout << endl;
}
}
}
|
The second solution is a "think less, but let recursion do the work" solution. You write a recursive procedure fill_next_digit(int index, int c_ok, string &s). What it does fill in the next digit with an 'A', a 'B', and a 'C' if c_ok is true. After each of these, it calls itself recursively to fill in the next digit. When index equals 10, it prints the string if c_ok is false (in other words, it doesn't print strings that don't have any 'C's). This one is in q5-recursive.cpp:
#include <string>
#include <iostream>
using namespace std;
void fill_in(int index, int c_ok, string &s)
{
if (index == 10) {
if (!c_ok) cout << s << endl;
return;
}
s[index] = 'A';
fill_in(index+1, c_ok, s);
s[index] = 'B';
fill_in(index+1, c_ok, s);
if (c_ok) {
s[index] = 'C';
fill_in(index+1, 0, s);
}
}
main()
{
int i, j, k;
string s;
s.resize(10, ' ');
fill_in(0, 1, s);
}
|
You could, of course, use a class so that you don't have to pass around the reference parameter.
Less good solutions: Some of you enumerated all 10-character strings with just A's and B's, and then for each of those, you printed out the ten strings that you get by replacing each character with 'C'. For that, you received a 2-point deduction, because you are generating a lot of duplicate strings.
Some of you inserted the above strings into a set and then traversed the set at the end. That's a nice way of cleaning up the solution, and you only lost a point for using an O(n log n) solution (where n is 2digits)) when an O(n) solution is available. I have that solution in q5-set.cpp.
Another approach was even less good was to enumerate all 310 ten-digit ABC-10 strings, and then only to print out those with exactly one C. That lost two points, because it is doing 115 times more work than it should (generating 310 strings and running through them to count C's, rather than generating 512 strings, and from them printing 10 strings each). I have that solution in q5-enum-3.cpp.
 |
#include <string>
#include <map>
#include <set>
#include <iostream>
using namespace std;
main()
{
map <string, set <string> > M;
set <string>::iterator sit;
string name, s, alias;
while (cin >> name) {
do {
cin >> s;
if (s != "XXX") {
name += " ";
name += s;
}
} while (s != "XXX");
cin >> alias;
M[name].insert(alias);
cout << name << ":";
for (sit = M[name].begin(); sit != M[name].end(); sit++) {
cout << " " << *sit;
}
cout << endl;
}
}
|
 |