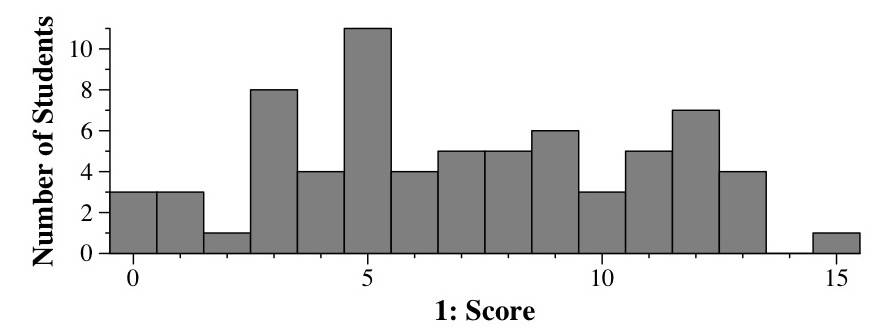
 |
 |
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | |
| A | 0 | 1 | 0 | 3 | 0 | 0 | 61 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| B | 0 | 15 | 0 | 5 | 0 | 0 | 1 | 0 | 47 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| C | 17 | 0 | 0 | 31 | 4 | 6 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| D | 0 | 3 | 0 | 53 | 0 | 0 | 0 | 0 | 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| E | 1 | 8 | 0 | 48 | 0 | 1 | 1 | 0 | 9 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| F | 0 | 2 | 0 | 1 | 0 | 2 | 0 | 0 | 2 | 2 | 58 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| G | 26 | 1 | 2 | 16 | 7 | 6 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| H | 0 | 0 | 1 | 1 | 3 | 2 | 0 | 0 | 0 | 1 | 1 | 60 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| I | 0 | 2 | 0 | 0 | 0 | 0 | 63 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 |
| J | 0 | 0 | 2 | 5 | 25 | 12 | 0 | 0 | 0 | 0 | 0 | 20 | 1 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| K | 1 | 5 | 0 | 55 | 0 | 0 | 5 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| L | 0 | 0 | 1 | 2 | 5 | 7 | 0 | 0 | 0 | 2 | 1 | 40 | 1 | 0 | 0 | 0 | 0 | 9 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| M | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 64 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| N | 0 | 1 | 1 | 0 | 2 | 4 | 0 | 0 | 0 | 0 | 0 | 60 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| O | 0 | 5 | 0 | 9 | 0 | 0 | 52 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
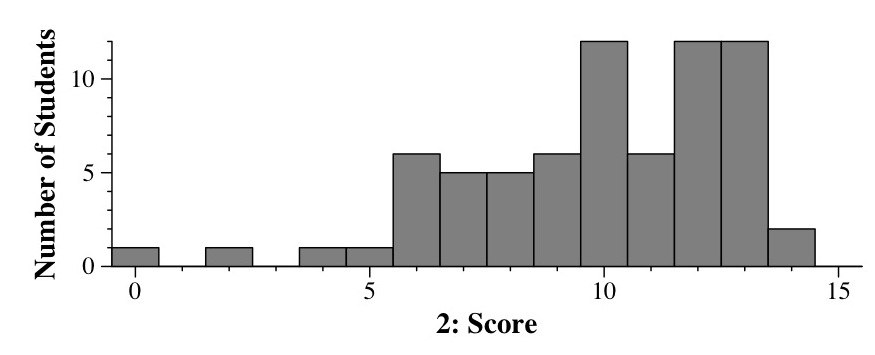 |
| A-1: No: | A-2: Yes: | A-3: Yes: | A-4: No: |
Part B:
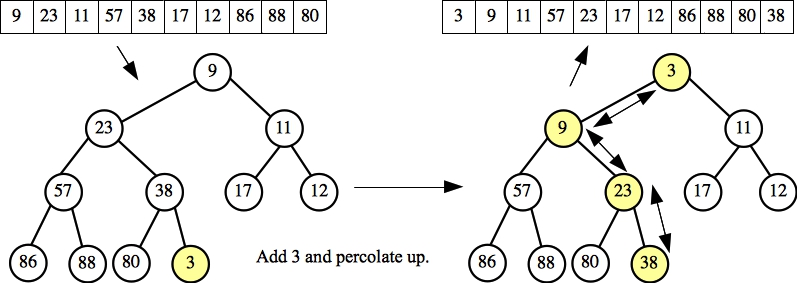 |
Part C:
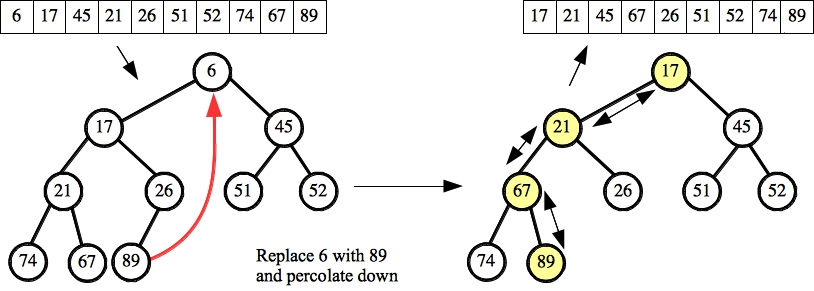 |
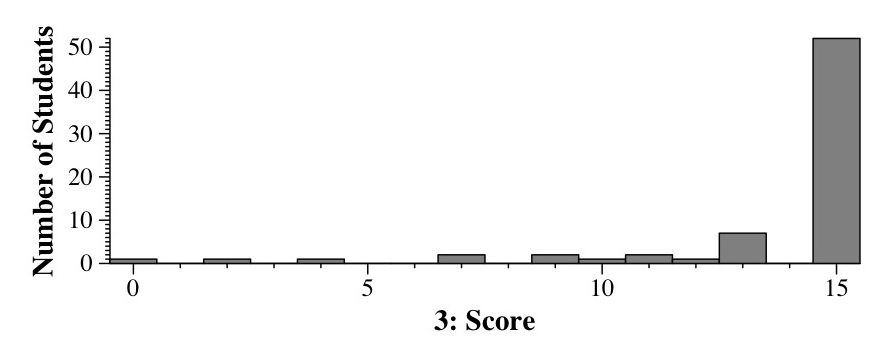 |
| Pass | Action | Result | Letter |
| 1 | Swap 10 with 10 (do nothing) | 10, 47, 99, 64, 77, 35, 56, 21 | w |
| 2 | Swap 21 with 47 | 10, 21, 99, 64, 77, 35, 56, 47 | j |
| 3 | Swap 35 with 99 | 10, 21, 35, 64, 77, 99, 56, 47 | g |
| 4 | Swap 47 with 64 | 10, 21, 35, 47, 77, 99, 56, 64 | e |
| 5 | Swap 56 with 77 | 10, 21, 35, 47, 56, 99, 77, 64 | d |
| 6 | Swap 64 with 99 | 10, 21, 35, 47, 56, 64, 77, 99 | a |
| 7 | Swap 77 with 77 (do nothing) | 10, 21, 35, 47, 56, 64, 77, 99 | a |
| 8 | Done | 10, 21, 35, 47, 56, 64, 77, 99 | a |
Insertion Sort
| Pass | Action | Result | Letter |
| 1 | Insert 47 (do nothing) | 10, 47, 99, 64, 77, 35, 56, 21 | w |
| 2 | Insert 99 (do nothing) | 10, 47, 99, 64, 77, 35, 56, 21 | w |
| 3 | Insert 64 | 10, 47, 64, 99, 77, 35, 56, 21 | v |
| 4 | Insert 77 | 10, 47, 64, 77, 99, 35, 56, 21 | u |
| 5 | Insert 35 | 10, 35, 47, 64, 77, 99, 56, 21 | o |
| 6 | Insert 56 | 10, 35, 47, 56, 64, 77, 99, 21 | n |
| 7 | Insert 21 | 10, 21, 35, 47, 56, 64, 77, 99 | a |
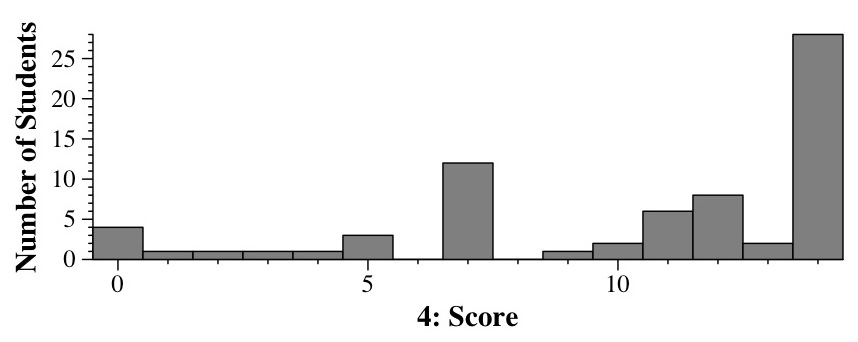 |
Disjoint::Disjoint(int nelements)
{
links.resize(nelements, -1);
ranks.resize(nelements, 1);
}
int Disjoint::Union(int s1, int s2)
{
int p, c;
if (ranks[s1] >= ranks[s2]) {
p = s1;
c = s2;
} else {
p = s2;
c = s1;
}
links[c] = p;
ranks[p] += ranks[c];
return p;
}
int Disjoint::Find(int element)
{
while(links[element] != -1) element = links[element];
return element;
}
|
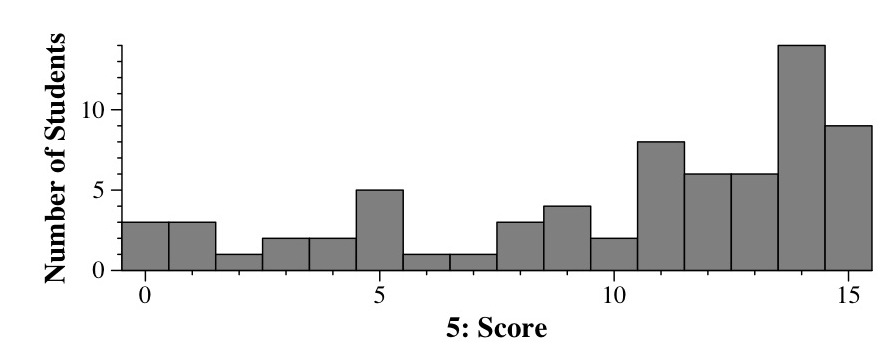 |
#include <iostream>
#include <cstdio>
#include <cstdlib>
using namespace std;
long long two_ks(int K, long long S)
{
long long rv;
if (K == 0) return 1 % S;
if (K%2 == 1) return (2 * two_ks(K-1, S)) % S;
rv = two_ks(K/2, S);
return (rv * rv) %S;
}
main()
{
int K;
long long S;
cin >> K >> S;
cout << two_ks(K, S) << endl;
exit(0);
}
|
 |