CS302 Midterm, Spring, 2017
James S. Plank
Answers and Grading
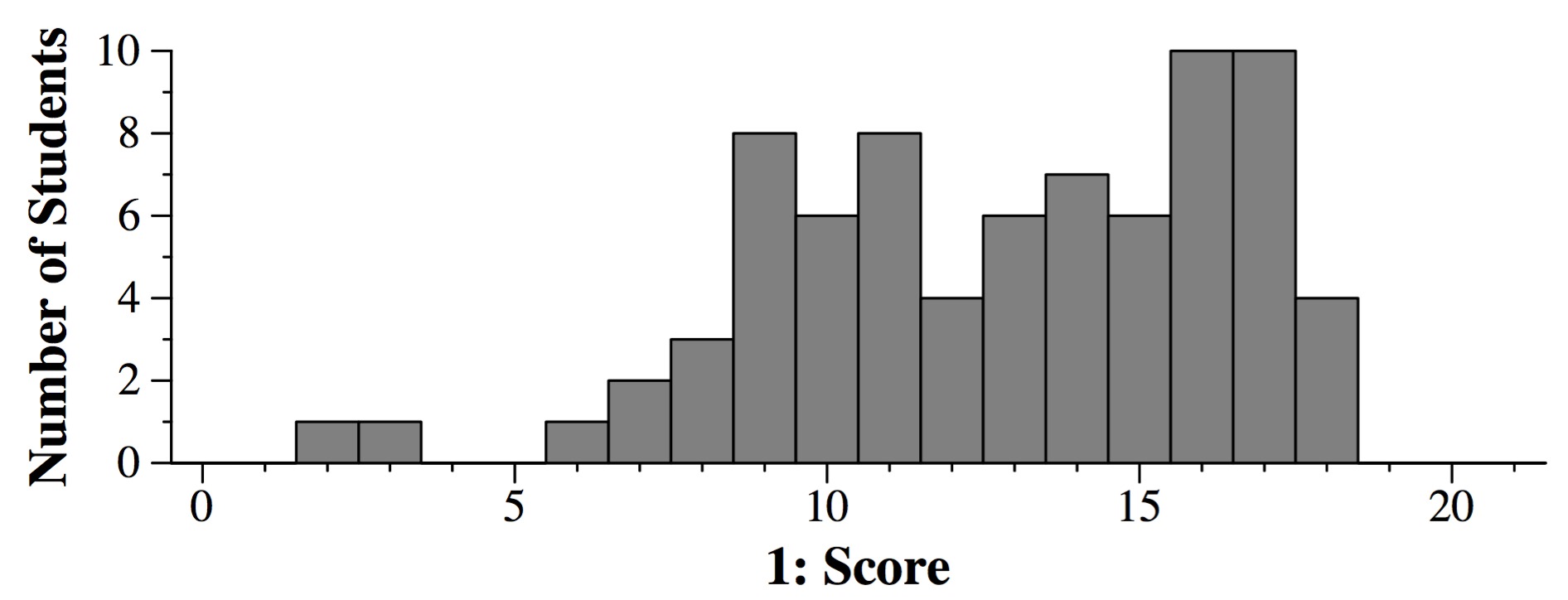
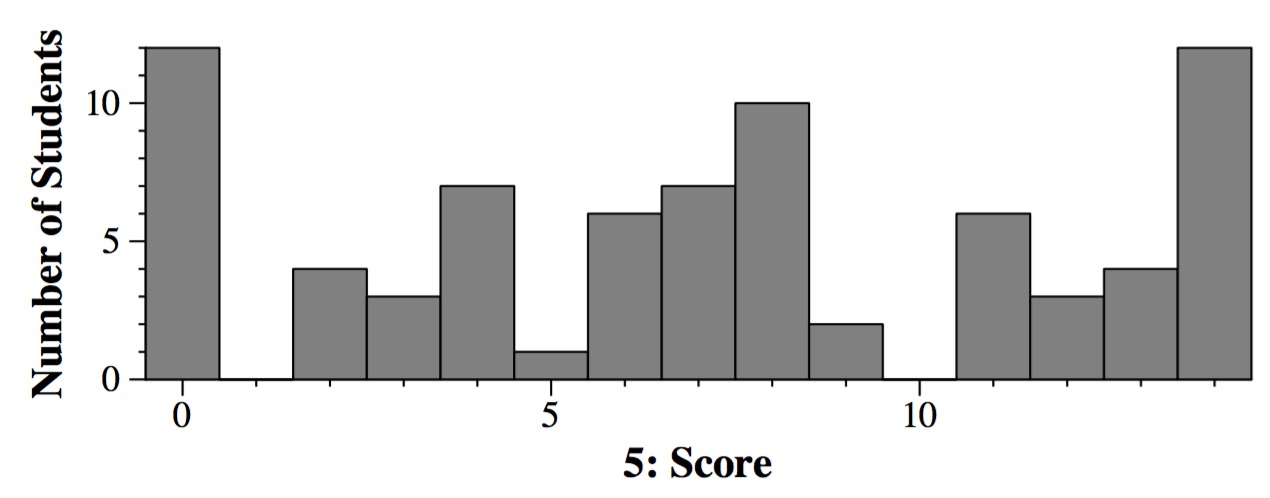
Question 1: 21 points
With the exception of part J, the majority answer from the class was right
in every circumstance. I have the percentage of correct answers with each part.
Grading: 1.4 points per part. I gave some partial credit, but not a large amount.
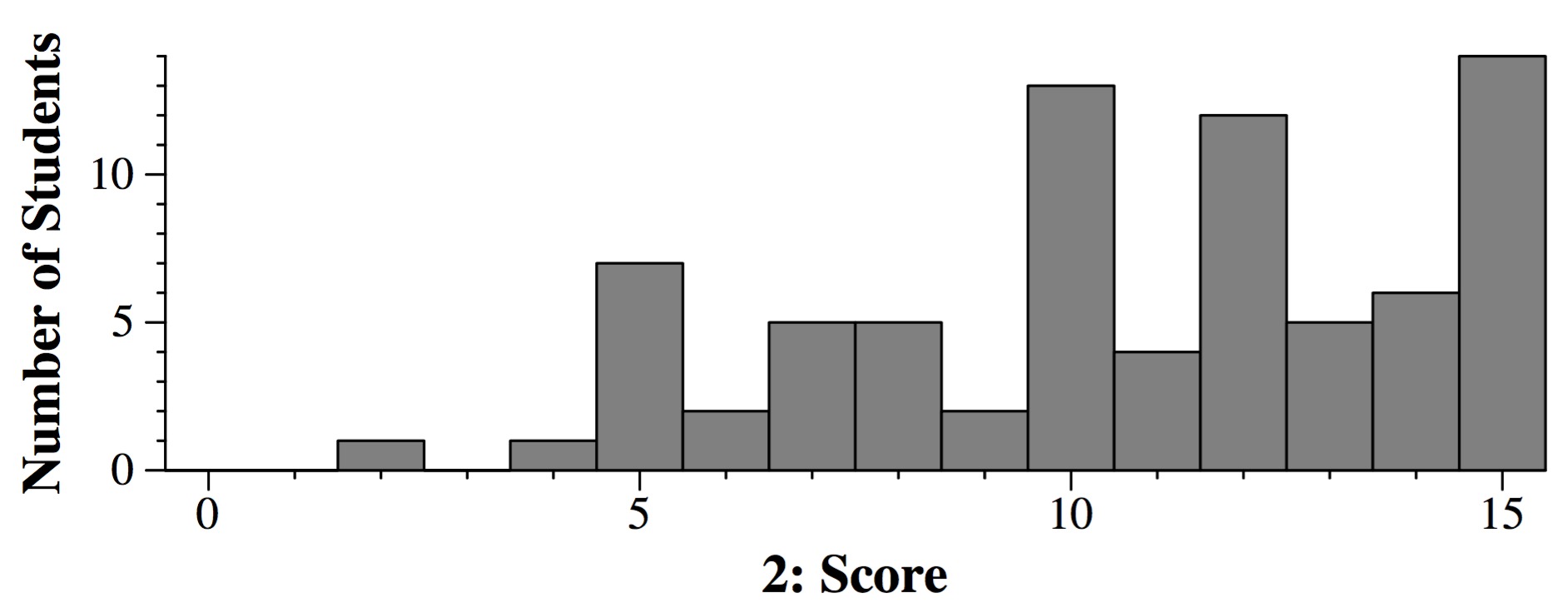
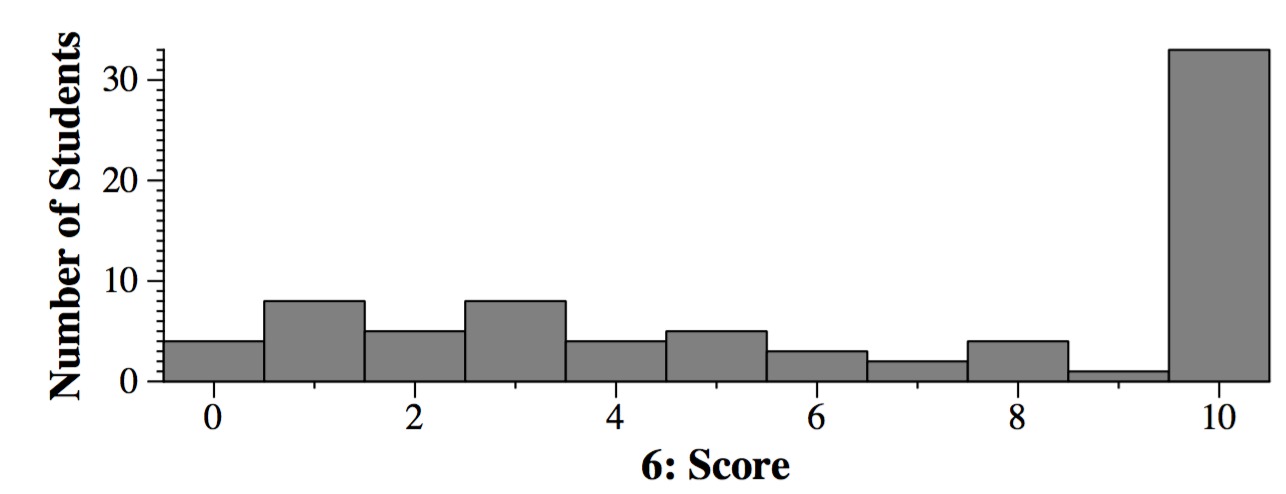
Question 2: 15 points
Again, crowdsourcing got the correct answer in each part.
- Part A: (92.2%) The answer is the number of permutations of the cities: 12!
- Part B: (68.8%) The number of 10-character strings from a 5-character
alphabet: (X%) 510.
- Part C: (81.8%) "12 choose 5", which is equal to "12 choose 7": (12!) / ( (5!) (7!) )
- Part D: (48.1%) That's a power set enumeration: 26.
- Part E: (66.2%) This is the number permutations of the 15 balls: 15!
- Part F: (40.3%) This is the number of ways to choose 5 elements from 23
elements: "23 choose 5", which is equal to "23 choose 18": (23!) / ( (5!) (18!) )
Grading: 2.5 points per part.
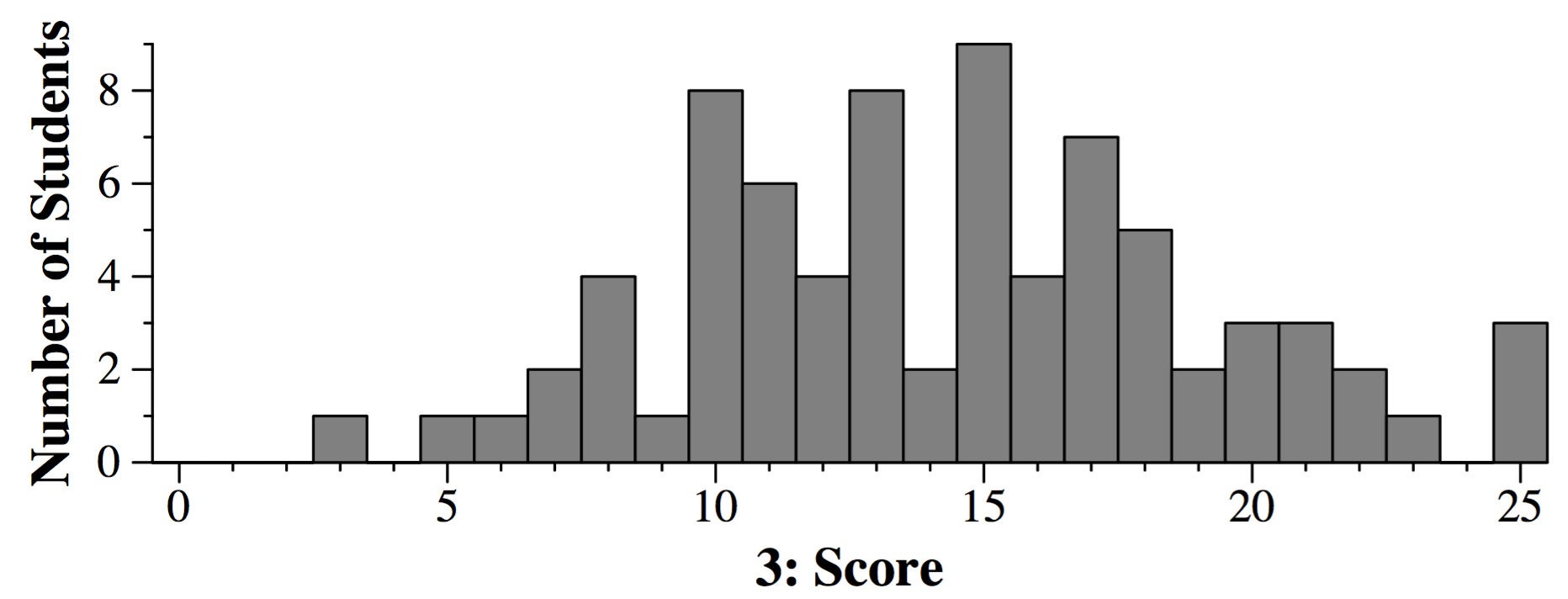
Question 3: 25 points
-
Part A: (89.6%) Here's the tree before and after the push operation:
The answer is: { 1, 2, 3, 6, 4, 3, 5, 8, 9, 7 }
-
Part B: (59.7%) Here's the tree before and after the pop operation:
The answer is: { 2, 3, 4, 5, 6, 8, 7, 9 }
-
Part C: (55.8%) This will swap 0 and 5, and then 1 and 6:
{ 0, 1, 3, 6, 2, 8, 5, 4, 7}
-
Part D: (48.1%) Depending on whether you start the outer for loop,
this will sort the first four or five elements of D fortunately,
the result is the same:
{ 0, 2, 4, 5, 6, 1, 3, 8, 7 }
-
Part E: (66.2%) This is the median of 7, 5 and 6: The answer is 6
-
Part F: (54.5%) You will swap 6 and 4, and 8 and 1. After that, the
partitioned vector is { 5, 0, 4, 2, 1, 3, 7, 8, 6 }. That's two swaps.
-
Part G: (33%) You will swap 6 and 2, and 8 and 6, and then 6 and 4.
After that, the
partitioned vector is { 6, 2, 0, 6, 4, 6, 8, 7, 2 }. That's three swaps.
-
Part H: (81.8%) Here's the data structure.
The answer is:
i set-id
- ------
0 5
1 5
2 5
3 3
4 5
5 5
6 5
7 7
8 3
-
Part I: The (31.1%) ranks vector changes if the two
sets have the same rank, so the answer is
7 and 3.
-
Part J: (18.2%) The head of the heap is its maximum value. That
means that element 7 starts the "sorted vector" part of the vector,
and that element 6 ends the heap. The answer is 7 (elements 0 through 6).
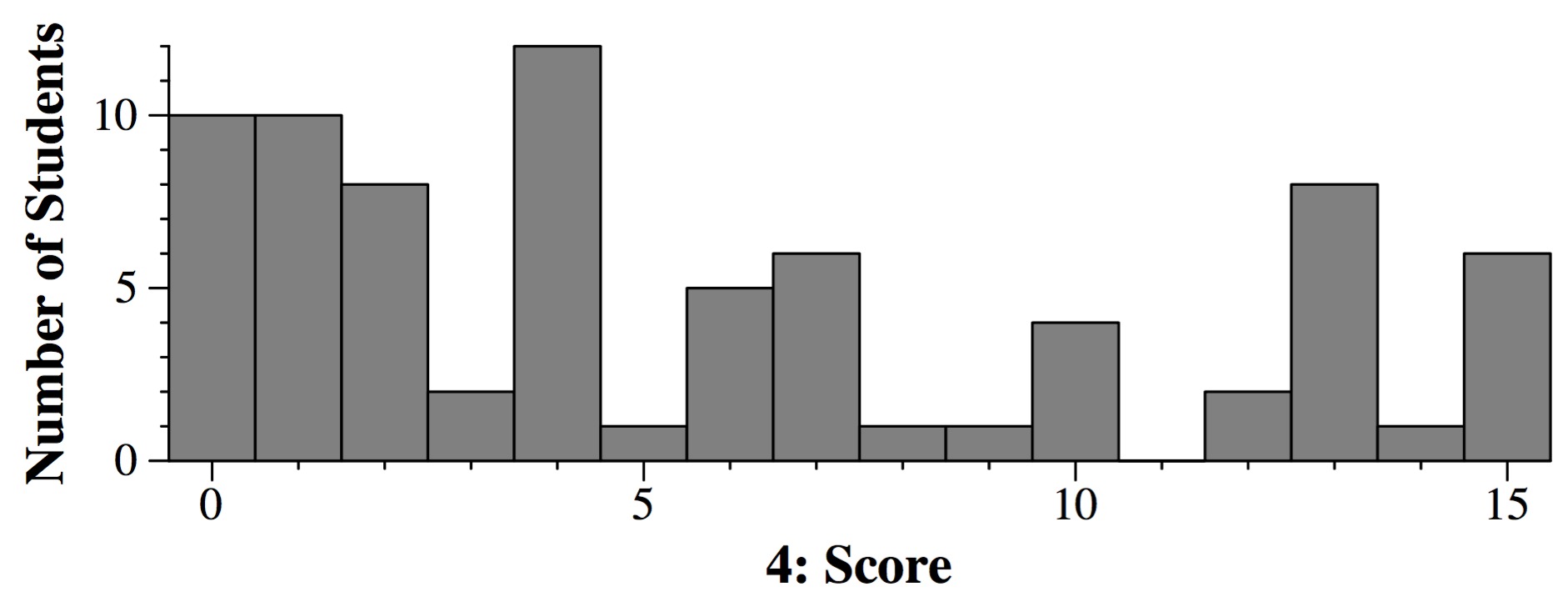
Question 4: 15 points
Part A: Each string A corresponds to a substring of S -- you simply need to sort the substring.
Another way of looking at it is to consider S to be a set of letters, and each string S
corresponds to a subset of S, printed in sorted order. Therefore, this is a power set
enumeration. The answer is 2n.
To code this up, first sort s, and then do a power set enumeration to enumerate subsets.
For each element in a subset, append it to a string, and after each subset, print the string and
clear it. The answer is in
q4.cpp, which has a main() that calls OSA with
the command line argument:
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cstdlib>
using namespace std;
void OSA(string s)
{
string a;
int i, j;
sort(s.begin(), s.end());
for (i = 0; i < (1 << s.size()); i++) {
a.clear();
for (j = 0; j < s.size(); j++) {
if (i & (1 << j)) a.push_back(s[j]);
}
cout << a << endl;
}
}
int main(int argc, char **argv)
{
if (argc != 2) { fprintf(stderr, "usage: q2 string\n"); exit(1); }
OSA(argv[1]);
return 0;
}
|
Grading: 15 points.
Question 5: 14 points
Both of these are straight from the lecture notes.
The easiest non-recursive way is to push the elements on the path to the set id onto
a vector, and then you run through the vector and set the links fields:
int Disjoint::Find(int element)
{
vector <int> q;
int i;
while (links[element] != -1) {
q.push_back(element);
element = links[element];
}
for (i = 0; i < q.size(); i++) links[q[i]] = element;
return element;
}
|
Recursion is even easier -- if you're the set id, you're done.
Otherwise, call Find() recursively on your link field, and
set your link field to the result:
int Disjoint::Find(int element)
{
if (links[element] == -1) return element;
links[element] = Find(links[element]);
return links[element];
}
|
Grading: 7 points per implementation.
Question 6: 10 points
Part A:
The variable sp points to the underlying string that is part
of s, right after s is set to "0123456789." In the
first two calls, the underlying string does not change its location,
which means that sp is still pointing it it. However, in the
third call, the string library changes where the underlying string
is, because the original string is not big enough to accommodate the
13 push_back() calls. That means that sp is no longer
pointing to the underlying string -- we don't know what it's pointing
to. What we know is that when we print it out, we get nothing.