CS302 Final Exam - Answers and Grading
James S. Plank - December 10, 2013
Question 1:
Part 1: With selection sort, you should be swapping the smallest element with the
first element at iteration 0, and the second-smallest element with the second
element at iteration 1.
With insertion sort, iteration 1 will sort the first two elements, and
iteration 2 will sort the first three elements.
It's possible for the output to be both.
- Output A: This is insertion sort.
- Output B: Also insertion.
- Output C: Selection. Iteration 0 could be either, but iteration 1
differentiates it.
- Output D: This is neither.
- Output E: Also neither.
- Output F: Selection.
Part 2: The median of the first, middle and last element is 619. So, we swap that to the
front:
619, 983, 036, 783, 734, 186, 494, 469, 251
We set l = 1 and r = 8. The elements at those pointers are in the wrong partition, so
we swap them:
619, 251, 036, 783, 734, 186, 494, 469, 983
We increment l until we get to an element that is too big: l=3.
And we decrement r until we get to an element that is too small: r=7.
And we swap:
619, 251, 036, 469, 734, 186, 494, 783, 983
One more increment and decrement. l = 4 and r = 6. Swap:
619, 251, 036, 469, 494, 186, 734, 783, 983
Increment l until it equals 6. Decrement r until it equals 5. You're done. Swap elements
0 and 5. Here's the final answer:
186, 251, 036, 469, 494, 619, 734, 783, 983
Grading
Part 1: 12 points -- two per part.
Part 2: 6 points -- rubrick as follows:
- Two points if you gave a valid partition about 251 or 619.
- Two more points if you gave a valid partition about 619.
- Two more points if you gave the partition in the correct order.
Question 2: Dynamic Programming
You need to add a cache. You need to test it in the beginning of gc(),
and whenever you return, you need to add the return value to the cache before
you return.
You don't need to do this in the first return statement, because there are no recursive
calls before that first return statement.
How you index the cache is a concern, because you need to index it both by the
string and by zero. In my answer code, I convert them both into a
string using a stringstream. However, you could have an array of two caches --
one for zero = 0, and one for zero = 1.
You cannot use a vector indexed on s.size(), because the string changes from
call to call (with news).
Here is an answer.
Grading:
- Did you add a cache: 3 points
- Was the cache keyed on s: 2 points
- Was the cache keyed on zer : 2 points
- Did you try to return an answer from the cache first: 3 points
- Correctly handling the second return: 2 points
- Correctly handling the last return: 3 points
Question 3: Network flow
You were asked to process an augmenting path through a graph while doing
network flow. That means you need to figure out the residual flow in the path,
and then subtract it from the residual, add the reverse flow to the residual,
and add the flow to the flow graph.
There is a subtlety in adding the flow to the flow graph -- if there is flow in
the reverse edge, you need to take flow out of the reverse edge, and then if there
is any left, you add it to the flow of the non-reverse edge.
void Graph::Process_Augmenting_Path(vector <Edge *> path)
{
int i, f;
Edge *e, *r;
/* Figure out the flow in the path */
f = path[0]->residual;
for (i = 1; i < path.size(); i++) {
if (path[i]->residual < f) f = path[i]->residual;
}
/* Add flow to the flow graph (which means you may have to reduce flow
on a reverse edge. Also process the residual -- add flow to the
reverse edge's residual, and subtract it from the edge's residual. */
for (i = 0; i < path.size(); i++) {
e = path[i];
r = e->reverse;
if (r->flow >= f) {
r->flow -= f;
} else {
e->flow = (f - r->flow);
r->flow = 0;
}
e->residual -= f;
r->residual += f;
}
}
|
Grading
Points were allocated roughly as:
- Calculating the flow: 5 points
- Subtracting the flow from the residual: 3 points
- Adding flow to the residual reverse edge: 3 points
- Adding flow to flow: 3 points
- Correctly handling positive flow along the reverse edge: 2 points.
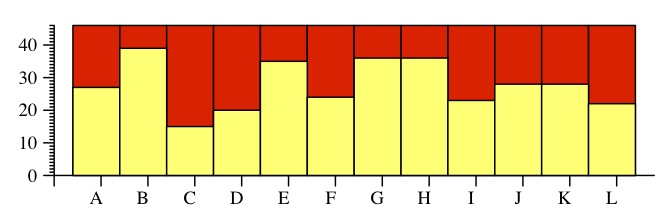
Question 4: Running Time
Because each node's adjacency list is ≤ 10, |E| = O(n). Thus, things
like O(|V| + |E|) become O(n), and O(|V|log(|E|)) become O(n log n).
- A: O(n log n).
- B: This is DFS: O(n).
- C: Power set -- you can represent a subset with an n-bit number: O(2n).
- D: Edmonds-Karp uses BFS: O(n).
- E: O(n)
- F: Dijkstra's algorithm: O(n log n)
- G: This is also DFS: O(n)
- H: O(n)
- I: The limiting activity is sorting the edges: O(n log n)
- J: This is BFS: O(n)
- K: This is the number of permutations: O(n!)
- L: O(n)
Grading
1.5 points per answer. There was a little partial credit:
- You got 1 point for O(n α(n)) on B.
- You got .5 points for O(n!) on C.
- You got .5 points for O(n α(n)) on I.
- You got .5 points for O(2n) on K.
Here are the individual answers -- red is wrong, yellow is right:
Question 5: Graph Algorithms
- Part A: The easiest thing here is to use Kruskal's algorithm, because
the edges are sorted already. You can draw the graph (or draw on top of the
graph in the question). You start with FI, DH, FH, AE, AG, HJ, and GJ. At that
point, here's the graph:
The edge EH is next, but it is within the same connected component, so we
throw it out. The next three edges, BC, BE and HL, also work:
At this point, the only node that is no longer in the spanning tree is node K, so we throw
out edges BE, HL, CI, EI and CE. The last edge is JK.
The answer is FI, DH, FH, AE, AG, HJ, GJ, BC, BE, HL, JK.
- Part B: When you start with node A, the multimap is:
(5,E),(6,G),(42,B),(84,C),(94,D)
We process node E (distance 5), which updates the multimap as:
(6,G),(16,H),(22,B),(28,I),(33,C),(49,F),(57,D)
We process node G (distance 6), which updates the multimap as:
(15,J)(16,H),(22,B),(28,I),(33,C),(49,F),(54,D),(82,K)
We've now reached J, so we're done. The final answer is:
(16,H),(22,B),(28,I),(33,C),(49,F),(54,D),(82,K)
- Part C:
You can do a Modified Dijkstra here, or frankly, you can eyeball the
adjacency matrix. The maximum edge incident to J has flow 85, and
the maximum edge incident to C is 84, so any path with a flow of
84 will be maximum. You can see that CA,AD,DJ has a flow of 84. That's it!
- Part D:
Keep a table of the maximum weight paths to B, C, D, E and F, and process
the nodes in that order:
|
Path to B |
Path to C |
Path to D |
Path to E |
Path to F |
| Process Node A |
42 (A->B) |
84 (A->C) |
94 (A->D) |
5 (A->E) |
- |
| Process Node B |
Done |
84 (A->C) |
140 (A->B->D) |
59 (A->B->E)/td>
| 95 (A->B->F) |
| Process Node C |
Done |
Done |
140 (A->B->D) |
112 (A->C->E) |
124 (A->C->F) |
| Process Node D |
Done |
Done |
Done |
192 (A->B->D->E) |
124 (A->C->F) |
| Process Node E |
Done |
Done |
Done |
Done |
236 (A->B->D->E->F) |
The answers are on the diagonal of the above table.
Grading
- 4 points for A
- 5 points for B
- 4 points for C
- 5 points for D