CS302 Final Exam - Answers and Grading

James S. Plank - December 9, 2015

Question 1

The procedure halt() takes two parameters. Program_file is the name of a file containing a C++ program. Input_file is the name of a file which program_file will read on standard input. The procedure halt() should take a finite amount of time to complete, and it should return "infinite loop" if it determines that program_file will go into an infinite loop when it runs input_file on standard input. It should return "halt" otherwise.

The halting problem states that it is impossible to write halt().

Grading

Question 2

Parts A-C: Just before the final merge, the first half of the array will be sorted, as will the second half. Here are the answers: To perform the partition, we will have two pointers, l and r, which start at elements 1 and size()-1 respectively. We increment l until it points to a value greater than or equal to the pivot, and we decrement r until it points to a value less than or equal to the pivot. We swap the values, increment l, decrement r and move on. So:

Grading:

2 points per. I gave some partial credit on the quicksort answers, so long as you partitioned the input correctly, and the pivot was in the beginning.

Question 3

We went over this exact problem in detail in class. It is in the Dynamic Programming lecture notes. The file Q3.cpp has an answer and a main(). Here's the answer: 

int MS::Maxseq_DP(int a, int b)
{
  int rv, rv1, rv2;

  if (a == SA.size()) return 0;
  if (b == SB.size()) return 0;

  if (cache[a][b] != -1) return cache[a][b];

  if (SA[a] == SB[b]) {
    rv = 1 + Maxseq_DP(a+1, b+1);
  } else {
    rv1 = Maxseq_DP(a, b+1);
    rv2 = Maxseq_DP(a+1, b);
    rv = (rv1 > rv2) ? rv1 : rv2;
  }
  cache[a][b] = rv;
  return rv;
}

We can verify it on examples from the lecture notes: 

UNIX> g++ Q3.cpp
UNIX> echo AbbbcccFyy FxxxyyyAc | a.out
3
UNIX> echo AbbbcccFyy FxxxyyyAccc | a.out
4
UNIX> echo 9009709947053769973735856707811337348914 9404888367379074754510954922399291912221 | a.out 
15
UNIX>

Grading

12 points. As usual, if you were close, you started with 12 points and I deducted for things that were incorrect. If you weren't close, I gave you points according to what I thought you did right.

Question 4

See relevant lecture notes for this.

Grading

As always, crowdsourcing scored 100% -- Y'all's answers:

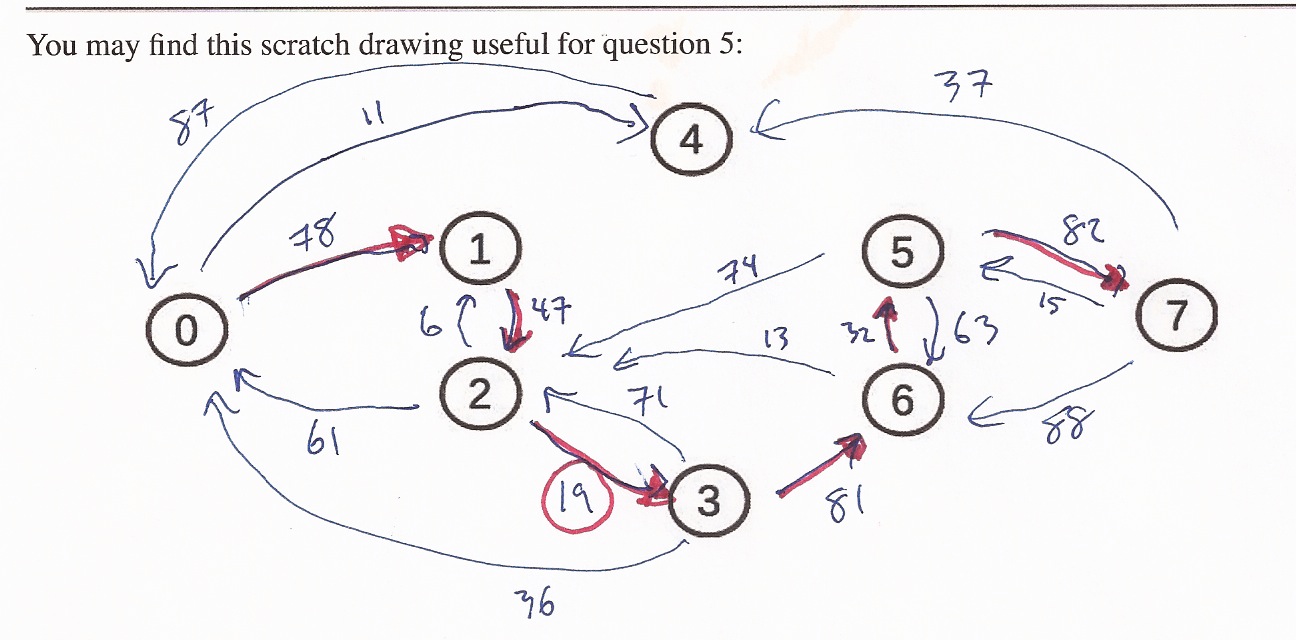
Question 5

Turn the adjacency matrix into a picture. Here's mine, using the node layout that I gave you on page two of the exam:

Part A: There's only one path from 0 to 7: 0 - 1 - 2 - 3 - 6 - 5 - 7.

Part B: Its flow is 19.

Here is Part C as a plain text table: 

Change   0   1   -19
Change   1   2   -19
Remove   2   3   
Change   3   6   -19
Change   6   5   -19
Change   5   7   -19
Add      1   0    19
Change   2   1   +19
Change   3   2   +19
Add      6   3    19
Change   5   6   +19
Change   7   5   +19

Grading

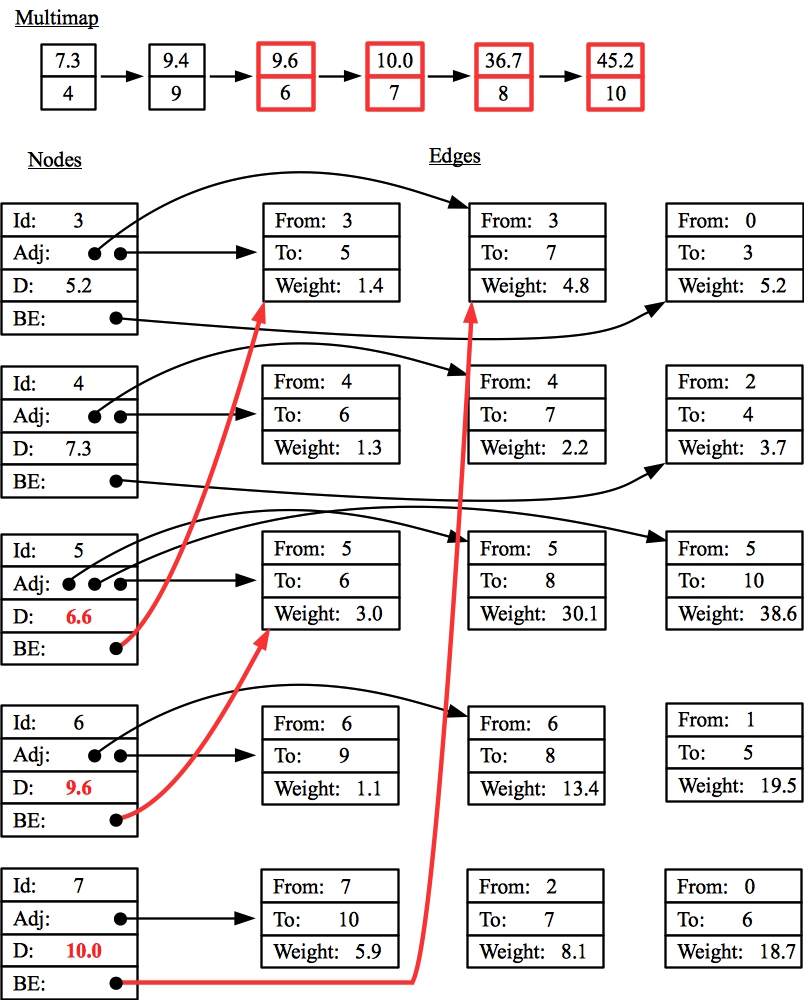
Question 6

Part A: Ptr is there for when you find a shorter path to a node than the one that is currently recorded on the multimap. When that happens, you have to delete the node from the multimap and reinsert it with the new path. The problem is that the entry on the multimap is keyed on distance and not on the node itself, so you retain a pointer to it in Ptr. That way, you can find the entry in the multimap in constant time, so that you may delete it.

Part B

. The first node that you process is node three: The next node on the multimap is now node 5, because its distance (6.6) is less than node 4's (7.3). So: Here's the drawing, with anything new/changed in red:

Grading