Hints for SRM 351, D2, 1000-Pointer (InsertSort)
James S. Plank
Sun Nov 3 12:32:31 EST 2013
Problem Statement.
Here's the thought that helped me solve the problem. Look at the first number.
If it's the smallest number, then that number will contribute zero to the solution.
Otherwise, you have two options to have that number hit its final resting place:
- You insert it there. Then you solve the rest of the problem.
- You insert all numbers less than it to their final resting places, adding
their sums to the weight. Then you can ignore the initial number and all of the
numbers that you moved, and solve the rest of the problem.
This thought leads to a shortest path solution, where we build the graph as we
process Dijkstra's algorithm. Each node will be labeled with a string that has
theArray.size() elements. Initially it will be all dashs.
We take the initial node and put it onto our multimap with a distance of zero.
We then process nodes as in Dijkstra's algorithm. Here's how we process a node
with string s and distance d.
- Find the first dash in s. Suppose it is at index i.
- If there is no dash, you're done.
- If the element is
the smallest of all other elements with dashs, then
create an edge to a node that has
an X at index i (you may have to create the node, or it may exist already).
The edge has weight 0. Put the node onto the multimap if the node isn't there
already, or if it is there and its distance is greater than d.
- Suppose it is not the smallest of all other elements. Then you are going to
have edges to two other nodes. The first is a node with an X at index i,
and its weight is the value of theArray[i]. The second is a node that has
an X at index i, and at all indices j where s[j] is a dash, and
theArray[j] is less than theArray[i]. The weight of the edge is the
sum of all of the theArray[j] elements.
Create those edges (and nodes) and put the nodes onto the multimap if you have to.
Here are graphs for some of the examples:
Example 0
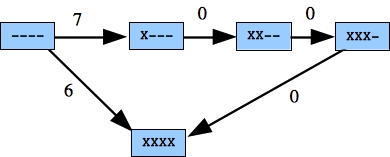 |
Example 1
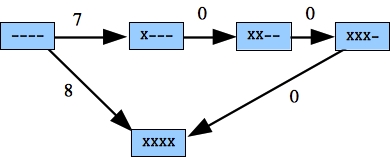 |
Example 3
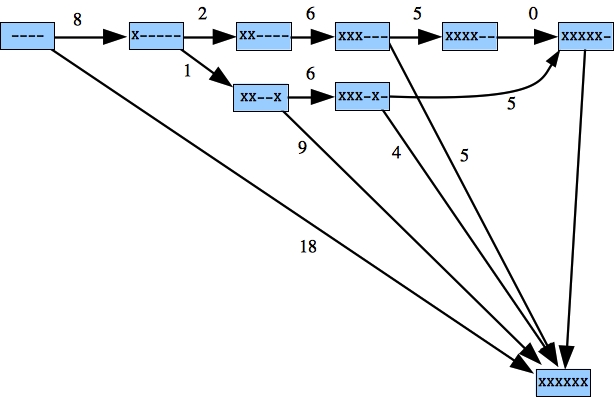 |



