 |
One of our alums, Camille Crumpton, sent me this journal entry of how a Bloom Filter drastically helped the writer with performance of a program that generated leaderboards on the fly.
And another alum, Even Ezell, sent me this link, where the author uses Bloom filters to "efficiently synchronize hash graphs."
Dr. Emrich sent me this link about using Bloom Filters in biological research: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5467106/.
The data structure of the Bloom Filter is a vector of m bits. When you start, they are all zero. When you want to insert an element into the Bloom Filter, you calculate k hash values of the element using k different hash functions. The hash values should be between 0 and m-1. Then, you set the bits corresponding to every hash value to one.
To query the Bloom Filter to see whether it contains the element, you again take the k hashes of the element. If all of the bits corresponding to these hashes are one, the answer is "yes." Otherwise, the answer is "no." It should be pretty clear that "no" answers are definitely correct, and "yes" answers can be wrong. The theoreticians have done the work to help you quantify how often you get incorrect "yes" answers. If there are n elements already inserted into the Bloom Filter, then the probability of an incorrect "yes" answer is:
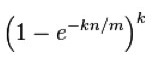 |
So, if you know n, you can choose m and k so that they satisfy whatever your tolerance is for incorrectness, while allowing to you adjust for space (m) and time (k).
Using the equation above, if we set k to 7, then our probability for incorrect "yes" answers is 0.00819. That's the best k for these values of n and m.
So, we are commiting 100MB for the Bloom Filter. If we hashed the downloads to 8-byte hash values, and stored them in hash table with a load factor of 0.5, then we'd need 1.28GB for our hash table. Our savings using a Bloom filter is at least a factor of 10, and to get that savings, we need to understand that 0.8% of our "yes" answers will be wrong. Those are some powerful savings.
Think about it this way -- suppose that the table is half full, and you want to look up an element. You have a 50% chance of getting a false positive with one hash function. When you add a second hash function, you only get a false positive if you have found a one bit with your first hash function (50%) and with your second hash function (another 50%). So your false positive probability is 25%. Add a third hash function, and that becomes 12.5%. Fourth = 6.25%. And so on. So, the equation above which relates k, m and n to the false positive rate embodies the tradeoff of filling the table faster versus being able to tolerate fuller tables with more hash functions. The second interpretation of this question is "But it's a pain to implement a whole bunch of hash functions. Can't I just use a really good hash function?" Yes, you can. If you have one really good hash function, then you can use it to create k hash values from a single piece of data, and that's what you need. You can do that in the following way -- add an extra byte to your data, and then if you need k hash values, you give that byte k different values, and use your hash function k times.
In the example program below, I use the MD5 hash function on the data. That is a hash function that returns a 16-byte hash value, and I only need four bytes because m is being held in an unsigned integer. So when I need k hash values, I do the following:
Our files are in f1.txt, f2.txt, f3.txt and f4.txt. They are each files containing 100 random names. Since m is 16, our hash function only needs to return values between 0 and 15. MD5 returns a 16-byte hash function, so we can simply use the first four bits as hash function 1, the next four bits as hash function 2, and the next four bits as hash function 3. Let's look at the hashes:
UNIX> openssl md5 f?.txt MD5(f1.txt)= 29295e325b77f8f822522728e795c1a4 MD5(f2.txt)= bcf9342184102dbd2107b7ba3cd4250e MD5(f3.txt)= 6559d5cb11a5ddab8573699ae360cb5a MD5(f4.txt)= faa43b30a66d00ba9b534a030ea09f88 UNIX>Here are the hash values:
f e d c b a 9 8 7 6 5 4 3 2 1 0 1 0 0 1 1 1 1 0 0 1 1 0 0 1 0 0
To test how well this works, I want to generate 100 random files, and see how many incorrect "yes" answers we get when we look up the files in the Bloom Filter. To do that, I've created one random file with 10,000 lines, and I use a shell script and sed to carve it up and test. The file is in f10000.txt. I use the (Bourne) shell script test-bloom-16.sh to create the 100 sets of three hashes, and put them into the file tmp.txt:
i=100 # "i" is the ending line to extract.
while [ $i -le 10000 ]; do
b=`echo $i | awk '{ print $1-99 }'` # Set the beginning line to extract.
sed -n $b,$i"p" f10000.txt | # Extract lines "b" to "i".
openssl md5 | # Use openssl to calculate the MD5 hash.
sed 's/(stdin)= \(...\).*/\1/' # Use sed to extract the first three characters
i=`echo $i | awk '{ print $1+100 }'` # Increment i by 100
done
|
UNIX> sh test-bloom-16.sh > tmp.txt UNIX> head tmp.txt eab 0b8 b41 3b9 843 649 31c 28e d6b 64b UNIX>I can now use sed, grep and wc to count the false positives.
UNIX> sed 's/[2569abcf]/x/g' tmp.txt | grep xxx | wc
12 12 48
UNIX>
12 false positives -- close enough to 14% to me! All in two bytes -- that's nice.
UNIX> gcc -o BF-tester BF-tester.c MOA.c -lcrypto UNIX> BF-tester usage: BF-Tester Seed Block_Size Reused_Blocks One_Off_Perc NEvents BF_Size(m) K Print(1|0) UNIX>On my Macintosh, I had to specify an additional include directory:
UNIX> gcc -o BF-tester -I/opt/local/include BF-tester.c MOA.c -lcryptoThe program simulates the Akamai example. We want to cache blocks, but we only want to cache them when they are used the second time, not the first. So, whenever we see a block, we'll check the Bloom Filter for it first. If it's there, we'll check the cache, and if it's not in the cache, we'd insert it into the cache. If the block is not in the Bloom Filter, we insert it, and move on.
This program doesn't actually manage a cache -- it simply manages the Bloom Filter, reporting false positives along the way.
Our program has the following parameters:
uint32_t MOA_Random_32(); /* Returns a random 32-bit number */
uint64_t MOA_Random_64(); /* Returns a random 64-bit number */
void MOA_Random_128(uint64_t *x); /* Returns a random 128-bit number */
uint32_t MOA_Random_W(int w, int zero_ok); /* Returns a random w-bit number. (w <= 32)*/
void MOA_Fill_Random_Region (void *reg, int size); /* reg should be aligned to 4 bytes, but
size can be anything. */
void MOA_Seed(uint32_t seed); /* Seed the RNG */
|
All straightforward. Is this better than the standard rand(), random() and rand48() of Unix? I'm guessing yes. I haven't done a thorough study of random number generators, but after a disaster using lrand48(), I won't use the Unix versions any more. If you want a nicer, C++ version of this, I have it implemented in a header-only library with some additional bells and whistles in http://web.eecs.utk.edu/~jplank/plank/classes/cs140/Notes/String/MOA.hpp.
The program is organized as follows. I allocate pointers to Reused_Blocks blocks of memory, and I initialize them to NULL. These are going to be the blocks that I repeat. Whenever I "reuse" a block, I choose a random number from 0 to Reused_Blocks-1 and look at the pointer. If it's NULL, then I create the block from random numbers. If it's not NULL, then I use the block that's there.
Each block consumes Block_Size+1 bytes -- you'll see why there's an extra byte below.
I also allocate one extra block of size Block_Size+1, and I'll use this this every time I create a new "One Off" block. When that happens, I'll fill this extra block randomly.
Whenever I generate a random block, and the Bloom Filter returns that it's already there, I have generated a false positive. If I reuse a block, and the Bloom filter returns that the block isn't there, then it's a false negative, which means I have a bug in my Bloom filter.
I count the false positives, the number of random blocks that I have generated (whether they are cached or not), and report the false postive rate.
All of that code is pretty straightforward, so I won't go over it here. I will go over how I use the MD5() function from the crypto library to generate all of the hashes, and how I do the bit arithmetic in the Bloom Filter.
The MD5() function takes a region of memory, its size, and a buffer of length MD5_DIGEST_LENGTH, which is 16. It calculates the hash and stores it in the buffer. I want to allow my tables to be pretty big, and I want to allow k to vary as well, so I am not going to assume that all k hashes can come from one MD5 hash. Instead, what I do is set the first byte of my block to zero, and use the MD5 hash of all block_size+1 bytes for the first 4 hash values, taking each as a 32-bit integer modulo BF_Size. I then set the first byte to one, and use the MD5 hash for the next 4 hash values, and so on. That way, k can be as large as 1024.
You can see the code below:
/* Call this procedure to set K hashes into hashes from the data in block. The size of
block is block_size (which includes the extra byte). The first byte of the block is
not data -- you get to use it when you need to calculate more than 4 hashes. */
void get_hashes_from_block(uint8_t *block, uint32_t *hashes, int K, int M, int block_size)
{
uint8_t md5_hash[MD5_DIGEST_LENGTH]; // Buffer for the MD5 hash.
int hc; // Counter for the extra byte
int sb_in_hash; // Starting byte for the next hash from the buffer.
int i;
hc = 0;
sb_in_hash = MD5_DIGEST_LENGTH;
for (i = 0; i < K; i++) {
if (sb_in_hash >= MD5_DIGEST_LENGTH) {
block[0] = hc;
hc++;
sb_in_hash = 0;
MD5(block, block_size, md5_hash);
}
memcpy(hashes+i, md5_hash+sb_in_hash, sizeof(int));
hashes[i] %= M;
if (PRINT) printf(" %0*x", bfhexdigits, hashes[i]);
sb_in_hash += sizeof(int);
}
}
|
To look up hashes in the Bloom Filter, I have a procedure called are_hashes_set(). The Bloom Filter itself is stored as an array of unsigned bytes. Looking up a hash it a simple matter of finding the proper byte, and performing an AND with the proper bit:
int are_hashes_set(uint8_t *BF, unsigned int *hashes, int k)
{
int i;
int index;
int shift;
for (i = 0; i < k; i++) {
index = hashes[i] / 8; // Yes, I could use bit arithmetic,
shift = hashes[i] % 8; // but a good compiler should do it for you.
if ((BF[index] & (1 << shift)) == 0) return 0;
}
return 1;
}
|
Setting hashes is very similar, and is done in the procedure set_hashes().
void set_hashes(uint8_t *BF, unsigned int *hashes, int k)
{
int i;
int index;
int shift;
for (i = 0; i < k; i++) {
index = hashes[i] / 8;
shift = hashes[i] % 8;
BF[index] |= (1 << shift);
}
}
|
Let's explore a little. First, let's do a small example so we can see the table. Let's have the table size be 16. We'll have one block that we reuse. We'll generate 10 events, half of which are to new blocks and half of which are to the block that we reuse. Oh, and our blocks will be 1K (it really doesn't matter how big they are), and we'll have three hashes per block:
UNIX> BF-Tester 1 1024 1 50 10 16 3 1 NEW 9 0 e ADDED 10000000 01000010 NEW 0 f 7 ADDED 10000001 01000011 NEW 2 c 0 ADDED 10100001 01001011 OLD 0 f 7 FOUND 10100001 01001011 OLD 0 f 7 FOUND 10100001 01001011 NEW a f d ADDED 10100001 01101111 OLD 0 f 7 FOUND 10100001 01101111 NEW d f 9 FOUND 10100001 01101111 OLD 0 f 7 FOUND 10100001 01101111 N: 5. False_positives: 1. Rate: 0.200000 UNIX>All of this should be pretty straightforward. You can see the false positive was the block that hashed to "d f 9". You can see that all of those bits are in the Bloom Filter.
Let's try a more realistic example. The Wikipedia page says that if you set your Bloom Filter's size to 10 times the number of elements that it will hold, and you set k optimally, then your false positive rate will be less than one percent. Let's generate 100,000 events with a One-Off percentage of 75. Let's have the number of blocks that will end up being cached be 5,000. That means of our 100,000 events, we'll have roughly 75,000 unique blocks and 5,000 cached blocks. So our Bloom Filter will hold 80,000 elements, and its size should be 800,000 bits. That's roughly 100K for the Bloom Filter.
I've written a small program in findk.c that calculates k values using the equation above. This gives us a way to test whether theory will match practice:
UNIX> findk usage: findk n(elements) m(bits in table) UNIX> findk 80000 800000 1 0.0952 2 0.0329 3 0.0174 4 0.0118 5 0.0094 6 0.0084 7 0.0082 8 0.0085 UNIX>Let's try it out:
UNIX> sh sh-3.2$ for i in 1 2 3 4 5 6 7 8 ; do > BF-tester 1 1024 5000 75 100000 800000 $i 0 > done N: 79997. False_positives: 3735. Rate: 0.046689 N: 79997. False_positives: 898. Rate: 0.011225 N: 79997. False_positives: 356. Rate: 0.004450 N: 79997. False_positives: 225. Rate: 0.002813 N: 79997. False_positives: 155. Rate: 0.001938 N: 79997. False_positives: 131. Rate: 0.001638 N: 79997. False_positives: 124. Rate: 0.001550 N: 79997. False_positives: 106. Rate: 0.001325 sh-3.2$ exit UNIX>Well, that seems to be better than theory, doesn't it? This vexed me for quite a while, until I realized that the theory is for a Bloom Filter that already has n elements. I am incrementally filling the Bloom Filter, which means that each time I add an element to the Bloom Filter, my rate changes.
So, let's copy findk.c to findinck.c and have it average the rates for every value of i from 0 to n-1. Now, theory matches practice!!
UNIX> findinck 80000 800000 1 0.0484 2 0.0115 3 0.0048 4 0.0027 5 0.0019 6 0.0015 7 0.0013 8 0.0013 9 0.0013 UNIX>I love it when it works. Chances are no student has read this far, but if you have, you should know that I had three different bugs in my BF-tester that cost me about 3 hours to find and fix, and the only reason that I knew to look for them was that the theory wasn't matching practice. Take that as a lesson in double-checking your code, because had I not double-checked with theory, I would have assumed it worked (my bugs made the Bloom Filter not work well -- one produced bad hashes from the MD5 hash, and the other was a bit arithmetic bug which made the Bloom Filter less efficient).