Dining Philosophers
The dining philosophers problem is a ``classical'' synchronization problem first posed by Edsger Dijkstra. Taken at face value, it is a pretty meaningless problem, but it is typical of many synchronization problems that you will see when allocating resources in operating systems.The book (again, chapter 6) has an excellent description of dining philosophers. I'll be a little more sketchy.
The problem is defined as follows: There are 5 philosophers sitting at a round table. Between each adjacent pair of philosophers is a chopstick. In other words, there are five chopsticks. Each philosopher does two things: think and eat. The philosopher thinks for a while, and then stops thinking and becomes hungry. When the philosopher becomes hungry, he/she cannot eat until he/she owns the chopsticks to his/her left and right. When the philosopher is done eating he/she puts down the chopsticks and begins thinking again.
Of course, the definition of this problem always leads me to ask a few questions:
- If these philosophers are so smart, shouldn't they be worried about communicable diseases?
- Why chopsticks? For some reason I envision philosophers liking soup.
- Evidently conversing isn't in here -- why do they need to be at the same table? I'm not sure if I'd enjoy having a philosopher philosophize while I'm eating. But then again, I'm not a philosopher.
- Shouldn't bathing be in the equation somewhere?
The challenge in the dining philosophers problem is to design a protocol so that the philosophers do not deadlock (i.e. every philosopher has a chopstick), and so that no philosopher starves (i.e. when a philosopher is hungry, he/she eventually gets the chopsticks). Additionally, our protocol should try to be as efficient as possible -- in other words, we should try to minimize the time that philosophers spent waiting to eat.
In case you're bored, here is that last paragraph in the inimitable words of professor Wolski: ``Since these are either unwashed, stubborn and deeply committed philosophers or unwashed, clueless, and basically helpless philosophers, there is a possibility for deadlock. In particular, if all philosophers simultaneously grab the chopstick on their left and then reach for the chopstick on their right (waiting until one is available) before eating, they will all starve. The challenge in the dining philosophers problem is to design a protocol so that the philosophers do not deadlock (i.e. the entire set of philosophers does not stop and wait indefinitely), and so that no philosopher starves (i.e. every philosopher eventually gets his/her hands on a pair of chopsticks).''
Dining Philosophers Testbed with CBThreads
What I've done is hack up a general driver for the dining philosophers problem using CBThreads, and then implemented several "solutions". Thus, it is structured like your labs. The main simulation is called with the following parameters:usage: dphil nphilosophers thinkavg eatavg sticktime interval duration seed verbose |
The parameteres are as follows:
- nphilosophers: The number of philosophers. The typical setting is 5, but the problem becomes more interesting when the number of philosophers is a big number.
- thinkavg: The average time that a philosopher thinks. These will be generated according to a uniform distribution from zero to thinkavg*2.
- eatavg: The average time that a philosopher eats. These will be generated according to a uniform distribution from zero to eatavg*2.
- sticktime: The time that it takes a philosopher to pick up a chopstick. This is also the time that it take a philosopher to put down a chopstick. In the canonical specification of the problem, there is no "sticktime," but it makes the problem more interesting and challenging.
- interval: This will print out statistics at a given interval of time.
- duration: This is the duration of the simulation. At the end of the simulation, statistics are printed.
- seed: Seed for srand48().
- verbose: If yes, this will print out the philosopher's actions. Otherwise, only the statistics are printed.
The driver is in dphil_skeleton.c and there is a header file in dphil.h. First, let's go over the header file:
|
The driver is pretty straightforward. It reads the simulation parameters and creates a Philosopher struct for each philosopher. All the philosophers are available in the p array of the Simulation struct. Before forking any threads, it calls initialize_simulation() so that you can add any state that you want in the v field.
Then it forks off the philosopher threads.
The philosopher threads of course have to use continuations when they block, and what we do is always call philosopher() as our continuation. Philosopher() checks the state of the philosopher and does the correct thing. There are six states. Here is what philosopher() does in each:
- STARTING: Calculate a random thinking time, set the state to THINKING
and sleep for that time (all sleeping is "fake").
- THINKING: Set the state to HUNGRY and call i_am_hungry(), which
you define. I_am_hungry() is blocking. When it unblocks it should call philosopher(p),
the philosopher's state should be GOTSTICKS, and the philosopher should have picked up the
chopsticks using pick_up_stick().
- GOTSTICKS: Calculate a random eating time, set the state to EATING
and sleep for that time (all sleeping is "fake").
- EATING: Set the state to SATED and call i_am_sated(), which you define. I_am_sated() is also blocking. When it unblocks it should call philosopher(p), the philosopher's state should be STARTING, and the philosopher should have put down the chopsticks using put_down_stick().
There are two other procedures defined in dphil_skeleton.c.
- pick_up_stick(Philosopher *p, int stick, void (*func)()): You are to call this when a philosopher wants
to pick up the specified chopstick (numbered 0 through nphil-1). This procedure double-checks to make sure
that the chopstick is free, and then sleeps for sticktime seconds. When it awakes, it calls the
given continuation function on p.
- put_down_stick(Philosopher *p, int stick, void (*func)()): This is just like pick_up_stick(), except the puts the stick down.
What you define
You define initialize_simulation(), i_am_hungry() and i_am_sated(). Their definitions are above, but I'll restate them:
- initialize_simulation(Simulation *s): This allows you to set up s->v any way you want.
- i_am_hungry(Philosopher *p): The philosopher's state will be HUNGRY. You need to write this so
that it never returns. Instead, it will call philosopher(p) with the following:
- The philosopher's state will be GOTSTICKS.
- The philosopher will have called pick_up_stick() on sticks p->id and (p->id+1)%p->s->nphil.
- i_am_sated(Philosopher *p): The philosopher's state will be SATED. You need to write this so
that it never returns. Instead, it will call philosopher(p) with the following:
- The philosopher's state will be STARTING.
- The philosopher will have called put_down_stick() on sticks p->id and (p->id+1)%p->s->nphil.
To be successful, your implementation will guarantee that two adjacent philosophers do not pick up the same chopstick. It should also have the following properties:
- The philosophers should not deadlock (where each holds one chopstick and is waiting for the other).
- No philosophers should starve (when one is hungry, he will eventually be able to eat).
- It should be fair (no philosopher should be favored).
- It should be as efficient as possible (the philosophers' blocking times should be minimized).
Solution #1: The Null Solution
The first solution is to have all three procedures do nothing. It is in dphil_1.c:
void i_am_hungry(Philosopher *p)
{
return;
}
void i_am_sated(Philosopher *p)
{
return;
}
void initialize_simulation(Simulation *s)
{
return;
}
|
Of course it compiles, but it doesn't run correctly. Here's an example where the philosophers think and eat for an average of three seconds, and it takes one second to pick up and put down the chopsticks:
UNIX> dphil_1 5 3 3 1 10 10 0 yes
0.000: 000 Thinking for 1.025.
0.000: 001 Thinking for 4.499.
0.000: 002 Thinking for 0.578.
0.000: 003 Thinking for 5.223.
0.000: 004 Thinking for 3.464.
0.578: 002 Hungry.
Error: i_am_hungry(2) returned
UNIX>
The first philosopher to call i_am_hungry() is philosopher 2, and since i_am_hungry() just
returns, that is flagged as an error.
Solution #2: Just try to grab those sticks
The second solution, in dphil_2.c simply has each philosopher just try to grab the chopsticks. Since pick_up_sticks() and put_down_sticks() are blocking, this needs to be continuation based, and to do that, I add a second state for each philosopher. This is in the array my_states, which is held in s->v. So, initialize_simulation() allocates the array and sets all states to BEGIN. Then i_am_hungry() works according to the states:
- If the state is BEGIN, set the state to GOT_STICK_1 and call pick_up_stick() on stick p->id.
- If the state is GOT_STICK_1, set the state to GOT_STICK_2 and call pick_up_stick() on stick (p->id+1)%p->s->nphil.
- If the state is GOT_STICK_2, then we're done. Set the state to BEGIN, set p->state to GOTSTICKS and call philosopher(p).
I_am_sated() works analogously.
#define BEGIN 0
#define GOT_STICK_1 1
#define GOT_STICK_2 2
typedef struct {
int *my_pstates;
} MyPhil;
void initialize_simulation(Simulation *s)
{
MyPhil *m;
int i;
m = talloc(MyPhil, 1);
m->my_pstates = talloc(int, s->nphil);
for (i = 0; i < s->nphil; i++) {
m->my_pstates[i] = BEGIN;
}
s->v = (void *) m;
return;
}
void i_am_hungry(Philosopher *p)
{
MyPhil *m;
int s1, s2;
m = (MyPhil *) p->s->v;
s1 = p->id;
s2 = (p->id+1)%p->s->nphil;
if (m->my_pstates[p->id] == BEGIN) {
m->my_pstates[p->id] = GOT_STICK_1;
pick_up_stick(p, s1, i_am_hungry);
} else if (m->my_pstates[p->id] == GOT_STICK_1) {
m->my_pstates[p->id] = GOT_STICK_2;
pick_up_stick(p, s2, i_am_hungry);
} else {
p->state = GOTSTICKS;
philosopher(p);
cbthread_exit();
}
}
|
void i_am_sated(Philosopher *p)
{
MyPhil *m;
int s1, s2;
m = (MyPhil *) p->s->v;
s1 = p->id;
s2 = (p->id+1)%p->s->nphil;
if (m->my_pstates[p->id] == GOT_STICK_2) {
m->my_pstates[p->id] = GOT_STICK_1;
put_down_stick(p, s1, i_am_sated);
} else if (m->my_pstates[p->id] == GOT_STICK_1) {
m->my_pstates[p->id] = BEGIN;
put_down_stick(p, s2, i_am_sated);
} else {
p->state = STARTING;
philosopher(p);
cbthread_exit();
}
}
|
When we run this on the parameters above, it works for a little bit before failing:
UNIX> dphil_2 5 3 3 1 10 10 0 yes
0.000: 000 Thinking for 1.025.
0.000: 001 Thinking for 4.499.
0.000: 002 Thinking for 0.578.
0.000: 003 Thinking for 5.223.
0.000: 004 Thinking for 3.464.
0.578: 002 Hungry.
0.578: 002 Picking up stick 002
1.025: 000 Hungry.
1.025: 000 Picking up stick 000
1.578: 002 Picking up stick 003
2.025: 000 Picking up stick 001
2.578: 002 Eating for 4.715.
3.025: 000 Eating for 4.153.
3.464: 004 Hungry.
3.464: 004 Picking up stick 004
4.464: 004 Picking up stick 000
Error: pick_up_stick(0) called on a stick in use.
UNIX>
Philosopher's 0 and 2 are the first to wake up, and they successfull pick up their chopsticks and
start eating. By luck, philosopher 4 is the next to wake up, and he picks up stick 4, which is
the only stick available. However, when he tries to pick up stick 0, we get an error.
Although this solution is a bad one, there are times when it will work. For example, make the think times big and the eat/stick times small:
UNIX> dphil_2 4 50 1 1 200 200 0 no 200.000: Thinktime: 181.086 Eattime: 4.414 Blocked_time: 14.500 Philosopher 000: Think: 179.226 Eat: 4.774 Blocked: 16.000 Philosopher 001: Think: 183.570 Eat: 4.430 Blocked: 12.000 Philosopher 002: Think: 182.215 Eat: 3.785 Blocked: 14.000 Philosopher 003: Think: 179.335 Eat: 4.665 Blocked: 16.000 UNIX>By chance, we don't have any adjacent philosophers wanting to eat at the same time. If we extend the duration, there is a failure between the 200th and the 300th second:
UNIX> dphil_2 4 50 1 1 100 20000 0 no 100.000: Thinktime: 92.142 Eattime: 1.858 Blocked_time: 6.000 200.000: Thinktime: 181.086 Eattime: 4.414 Blocked_time: 14.500 Error: pick_up_stick(1) called on a stick in use. UNIX>
Solution #3: Protect solution 2 with semaphores
The obvious way to implement mutual exclusion is with a semaphore initialized to one. dphil_3.c does this by adding a semaphore to every chopstick, and now the philosophers must call P() before calling pick_up_stick() and V() after calling put_down_stick(). Yes, continuations make this a pain, but by structuring the code around the philosopher's my_state, it's pretty straighforward. I'm only showing initialize_simulation() and i_am_hungry():
#define BEGIN 0
#define GOT_STICK_1 1
#define GOT_STICK_2 2
#define GOT_SEM_1 3
#define GOT_SEM_2 4
typedef struct {
cbthread_gsem *sems;
int *my_pstates;
} MyPhil;
void initialize_simulation(Simulation *s)
{
MyPhil *m;
int i;
m = talloc(MyPhil, 1);
m->my_pstates = talloc(int, s->nphil);
m->sems = talloc(cbthread_gsem, s->nphil);
for (i = 0; i < s->nphil; i++) {
m->sems[i] = cbthread_make_gsem(1);
m->my_pstates[i] = BEGIN;
}
s->v = (void *) m;
return;
}
|
void i_am_hungry(Philosopher *p)
{
MyPhil *m;
int s1, s2;
m = (MyPhil *) p->s->v;
s1 = p->id;
s2 = (p->id+1)%p->s->nphil;
if (m->my_pstates[p->id] == BEGIN) {
m->my_pstates[p->id] = GOT_SEM_1;
cbthread_gsem_P(m->sems[s1], i_am_hungry, p);
} else if (m->my_pstates[p->id] == GOT_SEM_1) {
m->my_pstates[p->id] = GOT_STICK_1;
pick_up_stick(p, s1, i_am_hungry);
} else if (m->my_pstates[p->id] == GOT_STICK_1) {
m->my_pstates[p->id] = GOT_SEM_2;
cbthread_gsem_P(m->sems[s2], i_am_hungry, p);
} else if (m->my_pstates[p->id] == GOT_SEM_2) {
m->my_pstates[p->id] = GOT_STICK_2;
pick_up_stick(p, s2, i_am_hungry);
} else {
p->state = GOTSTICKS;
philosopher(p);
cbthread_exit();
}
}
|
When we run this on our given example, it works fine:
UNIX> dphil_3 5 3 3 1 10 10 0 yes
0.000: 000 Thinking for 1.025.
0.000: 001 Thinking for 4.499.
0.000: 002 Thinking for 0.578.
0.000: 003 Thinking for 5.223.
0.000: 004 Thinking for 3.464.
0.578: 002 Hungry.
0.578: 002 Picking up stick 002
1.025: 000 Hungry.
1.025: 000 Picking up stick 000
1.578: 002 Picking up stick 003
2.025: 000 Picking up stick 001
2.578: 002 Eating for 4.715.
3.025: 000 Eating for 4.153.
3.464: 004 Hungry.
3.464: 004 Picking up stick 004
4.499: 001 Hungry. Note, philosopher's 4 and 1 are blocked here.
5.223: 003 Hungry. And now philosopher 3.
7.178: 000 Sated.
7.178: 000 Putting down stick 000
7.293: 002 Sated.
7.293: 002 Putting down stick 002
8.178: 000 Putting down stick 001 Now that pilosopher 0 has put down stick 0,
8.178: 004 Picking up stick 000 Philosopher 4 can pick it up.
8.293: 002 Putting down stick 003
9.178: 004 Eating for 2.213.
9.178: 000 Thinking for 5.243.
9.178: 001 Picking up stick 001
9.293: 002 Thinking for 4.471.
9.293: 003 Picking up stick 003
10.000: Thinktime: 3.264 Eattime: 1.938 Blocked_time: 4.798
Philosopher 000: Think: 1.847 Eat: 4.153 Blocked: 4.000
Philosopher 001: Think: 4.499 Eat: 0.000 Blocked: 5.501
Philosopher 002: Think: 1.285 Eat: 4.715 Blocked: 4.000
Philosopher 003: Think: 5.223 Eat: 0.000 Blocked: 4.777
Philosopher 004: Think: 3.464 Eat: 0.822 Blocked: 5.714
UNIX>
We can extend the simulation out, and it works. Is the blocked time good? We'll see later that it's not.
UNIX> dphil_3 5 3 3 1 10000 10000 0 no 10000.000: Thinktime: 1215.537 Eattime: 1199.599 Blocked_time: 7584.864 Philosopher 000: Think: 1213.645 Eat: 1199.705 Blocked: 7586.651 Philosopher 001: Think: 1272.240 Eat: 1225.338 Blocked: 7502.422 Philosopher 002: Think: 1216.960 Eat: 1202.474 Blocked: 7580.566 Philosopher 003: Think: 1221.017 Eat: 1177.727 Blocked: 7601.256 Philosopher 004: Think: 1153.821 Eat: 1192.751 Blocked: 7653.428 UNIX>Worse yet, this solution can deadlock. It doesn't here by chance, but a different seed does:
UNIX> dphil_3 5 3 3 1 10000 10000 21 yes
0.000: 000 Thinking for 2.746.
0.000: 001 Thinking for 3.278.
0.000: 002 Thinking for 3.622.
0.000: 003 Thinking for 3.878.
0.000: 004 Thinking for 1.975.
1.975: 004 Hungry.
1.975: 004 Picking up stick 004
2.746: 000 Hungry.
2.746: 000 Picking up stick 000
3.278: 001 Hungry.
3.278: 001 Picking up stick 001
3.622: 002 Hungry.
3.622: 002 Picking up stick 002
3.878: 003 Hungry.
3.878: 003 Picking up stick 003
10000.000: Thinktime: 3.100 Eattime: 0.000 Blocked_time: 9996.900
Philosopher 000: Think: 2.746 Eat: 0.000 Blocked: 9997.254
Philosopher 001: Think: 3.278 Eat: 0.000 Blocked: 9996.722
Philosopher 002: Think: 3.622 Eat: 0.000 Blocked: 9996.378
Philosopher 003: Think: 3.878 Eat: 0.000 Blocked: 9996.122
Philosopher 004: Think: 1.975 Eat: 0.000 Blocked: 9998.025
UNIX>
Whoops. Stubborn, starving, stupid philosophers.....
Solution #4: Asymmetry
One way to fix this problem is with asymmetry -- don't have every philosopher start with his or her left chopstick. A simple way to implement this is to have even numbered philosonphers start with chopstick p->pid and odd ones start with (p->pid+1)%p->s->nphil. In this way, you do not have circular waiting. The proof is fairly simple: With the exception of philospher zero, suppose a philosopher holds one chopstick but can't get the other. This means that the philosopher holding the other chopstick must be eating, and when that philosopher is done, the chopstick will be available. You can make similar proof about philosopher zero.We implement this in dphil_4.c. The only change to the code is in the beginning of i_am_hungry():
void i_am_hungry(Philosopher *p)
{
MyPhil *m;
int s1, s2;
m = (MyPhil *) p->s->v;
s1 = (p->id%2 == 0) ? p->id : (p->id+1)%p->s->nphil;
s2 = (p->id%2 == 1) ? p->id : (p->id+1)%p->s->nphil;
...
|
When we run it, we avoid the deadlock, and the blocktimes are lower:
UNIX> dphil_4 5 3 3 1 10000 10000 0 no 10000.000: Thinktime: 1982.282 Eattime: 1961.880 Blocked_time: 6055.838 Philosopher 000: Think: 2284.853 Eat: 2228.616 Blocked: 5486.531 Philosopher 001: Think: 1935.129 Eat: 1932.797 Blocked: 6132.074 Philosopher 002: Think: 1968.166 Eat: 1868.213 Blocked: 6163.622 Philosopher 003: Think: 1881.379 Eat: 1953.592 Blocked: 6165.029 Philosopher 004: Think: 1841.885 Eat: 1826.182 Blocked: 6331.933 UNIX> dphil_4 5 3 3 1 10000 10000 21 no 10000.000: Thinktime: 1944.159 Eattime: 1975.124 Blocked_time: 6080.717 Philosopher 000: Think: 2174.908 Eat: 2181.369 Blocked: 5643.723 Philosopher 001: Think: 1892.307 Eat: 1949.243 Blocked: 6158.449 Philosopher 002: Think: 1955.931 Eat: 1981.897 Blocked: 6062.171 Philosopher 003: Think: 1799.752 Eat: 1849.228 Blocked: 6351.020 Philosopher 004: Think: 1897.897 Eat: 1913.881 Blocked: 6188.223 UNIX>And if you look closely at each philosopher, you'll see that philosopher 0 is blocked less than the others. How does that scale when the table is bigger?
UNIX> dphil_4 11 3 3 1 10000 10000 0 no 10000.000: Thinktime: 1972.399 Eattime: 1984.463 Blocked_time: 6043.138 Philosopher 000: Think: 2173.933 Eat: 2269.385 Blocked: 5556.682 Philosopher 001: Think: 1931.846 Eat: 2018.246 Blocked: 6049.909 Philosopher 002: Think: 2014.558 Eat: 1981.562 Blocked: 6003.880 Philosopher 003: Think: 1969.787 Eat: 2051.790 Blocked: 5978.423 Philosopher 004: Think: 2005.238 Eat: 2016.456 Blocked: 5978.306 Philosopher 005: Think: 2042.704 Eat: 1915.682 Blocked: 6041.613 Philosopher 006: Think: 1986.464 Eat: 1911.700 Blocked: 6101.836 Philosopher 007: Think: 2006.558 Eat: 1980.617 Blocked: 6012.825 Philosopher 008: Think: 1972.216 Eat: 1962.954 Blocked: 6064.829 Philosopher 009: Think: 1823.299 Eat: 1873.342 Blocked: 6303.359 Philosopher 010: Think: 1769.784 Eat: 1847.361 Blocked: 6382.855 UNIX> dphil_4 11 3 3 1 100000 100000 21 no 100000.000: Thinktime: 19829.429 Eattime: 19908.143 Blocked_time: 60262.429 Philosopher 000: Think: 22670.207 Eat: 22307.138 Blocked: 55022.655 Philosopher 001: Think: 20018.830 Eat: 20065.023 Blocked: 59916.146 Philosopher 002: Think: 19751.059 Eat: 19853.586 Blocked: 60395.355 Philosopher 003: Think: 19989.986 Eat: 19951.486 Blocked: 60058.528 Philosopher 004: Think: 19712.115 Eat: 19902.039 Blocked: 60385.846 Philosopher 005: Think: 20022.446 Eat: 20052.777 Blocked: 59924.778 Philosopher 006: Think: 19688.739 Eat: 19900.370 Blocked: 60410.891 Philosopher 007: Think: 19803.414 Eat: 20128.918 Blocked: 60067.668 Philosopher 008: Think: 19832.591 Eat: 20018.772 Blocked: 60148.637 Philosopher 009: Think: 18357.009 Eat: 18434.129 Blocked: 63208.862 Philosopher 010: Think: 18277.321 Eat: 18375.330 Blocked: 63347.349 UNIX>Indeed, philosopher 0 is getting the best of all worlds -- she is blocked less, and therefore gets to eat more and think more. On the flip sides, philosohpers 9 and 10 seem to be getting a raw deal. It actually makes sense -- whenever philosopher 0 has to wait for a chopstick, it's because the adjacent philosopher is eating. Contrast that with philosopher 1. When that philosopher waits for chopstick 0, it may be the case that philosopher 0 is holding it and waiting for chopstick 10. That will translate to a longer wait time than philosopher 0's wait times.
The asymmetry prevents the deadlock, but unfortunately, it also causes unfairness. This will of course go away with an even number of philosophers, but with an odd number, philosopher 0 gets an unfair advantage.
Solution #5: The Book's Solution
The book's solution prevents deadlock and is fair. The algorithm is simple: only pick up the chopsticks when both are available. To implement this (dphil_5.c), we add an extra array to our system -- one that says whether the chopsticks are free. We have the same semaphores, but now we assign them to philosophers rather than to chopsticks. When a philosopher is hungry, he/she checks this array, and if both chopsticks are free, the philosopher sets them both as used, and then goes through the activity of picking them up. If the chopsticks aren't free, the philosopher sets his/her state to blocked and waits on his/her semaphore. We'll see how the philosopher is awakened in a bit. Here's the code for i_am_hungry():
typedef struct {
cbthread_gsem *sems;
int *sticks_free;
int *my_pstates;
} MyPhil;
void i_am_hungry(Philosopher *p)
{
MyPhil *m;
int s1, s2;
m = (MyPhil *) p->s->v;
s1 = p->id;
s2 = (p->id + 1) % p->s->nphil;
/* Block if you can't get both chopsticks */
if (m->my_pstates[p->id] == BEGIN && (!m->sticks_free[s1] || !m->sticks_free[s2])) {
m->my_pstates[p->id] = BLOCKED;
cbthread_gsem_P(m->sems[p->id], i_am_hungry, p);
}
if (m->my_pstates[p->id] == BEGIN) { /* If you can, then set them as used and pick them up */
m->sticks_free[s1] = 0;
m->sticks_free[s2] = 0;
m->my_pstates[p->id] = GOT_STICK_1;
pick_up_stick(p, s1, i_am_hungry);
} else if (m->my_pstates[p->id] == GOT_STICK_1) {
m->my_pstates[p->id] = GOT_STICK_2;
pick_up_stick(p, s2, i_am_hungry);
} else {
p->state = GOTSTICKS;
philosopher(p);
cbthread_exit();
}
}
|
Now, when a philosopher puts down a chopstick, he/she checks to see if the adjacent philosopher is blocked and if so, sets the philosopher's state back to BEGIN and wakes him/her up. It may not be the case that the philosopher can get both sticks, but the philosopher will check that upon waking up:
void i_am_sated(Philosopher *p)
{
MyPhil *m;
int s1, s2;
int before, after;
m = (MyPhil *) p->s->v;
s1 = p->id;
s2 = (p->id+1)%p->s->nphil;
if (m->my_pstates[p->id] == GOT_STICK_2) { /* Put down first stick */
m->my_pstates[p->id] = GOT_STICK_1;
put_down_stick(p, s1, i_am_sated);
} else if (m->my_pstates[p->id] == GOT_STICK_1) { /* Check the philosopher that shares s1 */
m->sticks_free[s1] = 1;
before = (p->id + p->s->nphil - 1) % p->s->nphil;
if (m->my_pstates[before] == BLOCKED) {
cbthread_gsem_V(m->sems[before]);
m->my_pstates[before] = BEGIN;
}
m->my_pstates[p->id] = BEGIN; /* Put down s2 */
put_down_stick(p, s2, i_am_sated);
} else {
m->sticks_free[s2] = 1;
after = (p->id + 1) % p->s->nphil; /* Check the philosopher that shares s2 */
if (m->my_pstates[after] == BLOCKED) {
cbthread_gsem_V(m->sems[after]);
m->my_pstates[after] = BEGIN;
}
p->state = STARTING;
philosopher(p);
cbthread_exit();
}
}
|
You may wonder -- why do I set an adjacent philosopher's state to BEGIN when calling cbthread_gsem_V()? The answer is subtle -- suppose philosophers 0 and 2 both stop eating simultaneously, with philosopher 0 executing first. If philosopher 0 didn't set philosopher 1's state to BEGIN when calling cbthread_gsem_V(), then philosopher 2 would also call cbthread_gsem_V() before philosopher 1 wakes up. That's wouldn't be good.
When we run it, we get a better blend: the philosophers eat more or less equally, and there's no deadlock:
UNIX> dphil_5 5 3 3 1 10000 10000 0 no 10000.000: Thinktime: 1835.950 Eattime: 1860.157 Blocked_time: 6303.893 Philosopher 000: Think: 1801.795 Eat: 1848.406 Blocked: 6349.799 Philosopher 001: Think: 1770.456 Eat: 1852.314 Blocked: 6377.231 Philosopher 002: Think: 1818.896 Eat: 1855.503 Blocked: 6325.601 Philosopher 003: Think: 1931.999 Eat: 1902.967 Blocked: 6165.034 Philosopher 004: Think: 1856.605 Eat: 1841.595 Blocked: 6301.800 UNIX> dphil_5 5 3 3 1 10000 10000 21 no 10000.000: Thinktime: 1836.099 Eattime: 1848.550 Blocked_time: 6315.351 Philosopher 000: Think: 1829.247 Eat: 1885.716 Blocked: 6285.037 Philosopher 001: Think: 1823.379 Eat: 1884.483 Blocked: 6292.138 Philosopher 002: Think: 1882.628 Eat: 1782.620 Blocked: 6334.752 Philosopher 003: Think: 1848.914 Eat: 1863.641 Blocked: 6287.445 Philosopher 004: Think: 1796.327 Eat: 1826.290 Blocked: 6377.382 UNIX> dphil_5 5 3 3 1 100000 100000 21 no | head -n 1 100000.000: Thinktime: 18461.891 Eattime: 18492.899 Blocked_time: 63045.210 UNIX>It doesn't perform as well as dphil_4 though. We'll discuss why later. It also has a very minor issue in that it can exhibit starvation. Consider the following sequence:
- Philosopher 0 is hungry and gets the chopsticks.
- Philosopher 4 is hungry and waits.
- Philosopher 2 is hungry and gets the chopsticks.
- Philosophers 1 and 3 are hungry and wait.
- Philosopher 2 is sated and puts down the chopsticks.
- Philosopher 3 now gets the chopsticks.
- Philosopher 0 is sated and puts down the chopsticks.
- Philosopher 1 now gets the chopsticks.
- Philosophers 0 and 2 are hungry and wait.
- Philosopher 1 is sated and puts down the chopsticks.
- Philosopher 0 now gets the chopsticks.
- Philosopher 3 is sated and puts down the chopsticks.
- Philosopher 2 now gets the chopsticks.
- Philosophers 1 and 3 are hungry and wait.
- Repeat from step 5
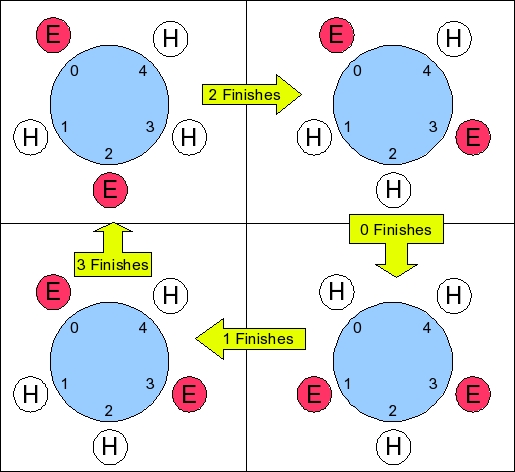 |
In dphil_skeleton_skew.c, I've modified the driver so that all the philosophers but philosopher 0 think for an extra second, philosophers 1 and 2 eat for an extra second, and the rest eat for an extra three seconds. When you call it with zero values for the think, eat and stick times, you get the scenario pictured above, and philosopher 4 starves:
UNIX> dphil_5_starve 5 0 0 0 5000 5000 0 no 5000.000: Thinktime: 0.800 Eattime: 1999.800 Blocked_time: 2999.400 Philosopher 000: Think: 0.000 Eat: 3750.000 Blocked: 1250.000 Philosopher 001: Think: 1.000 Eat: 1250.000 Blocked: 3749.000 Philosopher 002: Think: 1.000 Eat: 1250.000 Blocked: 3749.000 Philosopher 003: Think: 1.000 Eat: 3749.000 Blocked: 1250.000 Philosopher 004: Think: 1.000 Eat: 0.000 Blocked: 4999.000 UNIX>
Solution #6: Preventing Starvation
One way to ensure no starvation is to enforce an ordering on when the philosophers eat. A naive implementation of this is to use a queue. When a philosopher wants to eat, he/she gets appended to the queue. Then a philosopher can only eat if he/she is at the front of the queue with the chopsticks free.The implementation is straightforward again -- I've added a Dllist and a stated called QUEUED. Moreover, I've implemented a procedure called test_philosopher() which philosophers may use to test whether they or adjacent philosophers can eat (in dphil_6.c):
int test_philosopher(int pid, MyPhil *m, Simulation *s)
{
return (m->my_pstates[pid] == QUEUED &&
m->q->flink->val.i == pid &&
m->sticks_free[pid] &&
m->sticks_free[(pid+1)%s->nphil]);
}
|
In i_am_hungry(), a philosopher first appends himself/herself to the queue (q), and then calls test_philosopher() to determine whether or not to block.
In i_am_sated(), whenever a philosopher puts down a chopstick, he/she tests the adjacent philosopher to see if he/she can eat, and if so, calls cbthread_gsem_V() to wake that philosopher up:
void i_am_hungry(Philosopher *p)
{
MyPhil *m;
int s1, s2;
m = (MyPhil *) p->s->v;
s1 = p->id;
s2 = (p->id + 1) % p->s->nphil;
/* Put yourself on the queue initially */
if (m->my_pstates[p->id] == BEGIN) {
dll_append(m->q, new_jval_i(p->id));
m->my_pstates[p->id] = QUEUED;
}
/* Get the chopsticks if it's your turn */
if (test_philosopher(p->id, m, p->s)) {
dll_delete_node(m->q->flink);
m->sticks_free[s1] = 0;
m->sticks_free[s2] = 0;
m->my_pstates[p->id] = GOT_STICK_1;
pick_up_stick(p, s1, i_am_hungry);
/* Otherwise, block */
} else if (m->my_pstates[p->id] == QUEUED) {
cbthread_gsem_P(m->sems[p->id], i_am_hungry, p);
/* Get the second stick, etc. */
} else if (m->my_pstates[p->id] == GOT_STICK_1) {
m->my_pstates[p->id] = GOT_STICK_2;
pick_up_stick(p, s2, i_am_hungry);
} else {
p->state = GOTSTICKS;
philosopher(p);
cbthread_exit();
}
}
|
void i_am_sated(Philosopher *p)
{
MyPhil *m;
int s1, s2;
int before, after;
m = (MyPhil *) p->s->v;
s1 = p->id;
s2 = (p->id+1)%p->s->nphil;
/* Put down the first stick. */
if (m->my_pstates[p->id] == GOT_STICK_2) {
m->my_pstates[p->id] = GOT_STICK_1;
put_down_stick(p, s1, i_am_sated);
/* First stick is down, test adjacent philosopher. */
} else if (m->my_pstates[p->id] == GOT_STICK_1) {
m->sticks_free[s1] = 1;
before = (p->id + p->s->nphil - 1) % p->s->nphil;
if (test_philosopher(before, m, p->s))
cbthread_gsem_V(m->sems[before]);
m->my_pstates[p->id] = BEGIN;
put_down_stick(p, s2, i_am_sated);
/* Second stick is down, test adjacent philosopher. */
} else {
m->sticks_free[s2] = 1;
after = (p->id + 1) % p->s->nphil;
if (test_philosopher(after, m, p->s))
cbthread_gsem_V(m->sems[after]);
p->state = STARTING;
philosopher(p);
cbthread_exit();
}
}
|
When we run this, there's a problem -- everyone stalls. Let's take a look at when the seed is 4 because that's an easy example:
UNIX> dphil_6 5 3 3 1 500 500 4 yes
0.000: 000 Thinking for 3.924.
0.000: 001 Thinking for 3.410.
0.000: 002 Thinking for 0.301.
0.000: 003 Thinking for 4.395.
0.000: 004 Thinking for 3.180.
0.301: 002 Hungry.
0.301: 002 Picking up stick 002
1.301: 002 Picking up stick 003
2.301: 002 Eating for 3.898. Philosopher 2 eating.
3.180: 004 Hungry.
3.180: 004 Picking up stick 004
3.410: 001 Hungry.
3.924: 000 Hungry.
4.180: 004 Picking up stick 000
4.395: 003 Hungry.
5.180: 004 Eating for 4.043. Philosophers 2 & 4 eating. Q = 1,0,3
6.199: 002 Sated.
6.199: 002 Putting down stick 002
7.199: 002 Putting down stick 003 Philosopher 2 done. 1 can start
7.199: 001 Picking up stick 001
8.199: 001 Picking up stick 002
8.199: 002 Thinking for 5.133.
9.199: 001 Eating for 2.282. Philosophers 1 & 4 eating. Q = 0,3
9.223: 004 Sated.
9.223: 004 Putting down stick 004 Philosopher 4 done. 0 can't start yet.
10.223: 004 Putting down stick 000
11.223: 004 Thinking for 1.379.
11.481: 001 Sated.
11.481: 001 Putting down stick 001 Philosopher 1 done. 0 can start.
12.481: 001 Putting down stick 002
12.481: 000 Picking up stick 000
12.602: 004 Hungry.
13.332: 002 Hungry.
13.481: 000 Picking up stick 001
13.481: 001 Thinking for 0.400.
13.881: 001 Hungry.
14.481: 000 Eating for 1.393. Philosopher 0 eating. Q = 3,4,2,1
15.874: 000 Sated.
15.874: 000 Putting down stick 000 Philosopher 0 done. Only checks 4 & 1, not 3.
16.874: 000 Putting down stick 001
17.874: 000 Thinking for 1.996.
19.870: 000 Hungry. All philosophers on the queue.
500.000: Thinktime: 4.824 Eattime: 2.323 Blocked_time: 492.853
Philosopher 000: Think: 5.920 Eat: 1.393 Blocked: 492.687
Philosopher 001: Think: 3.810 Eat: 2.282 Blocked: 493.909
Philosopher 002: Think: 5.434 Eat: 3.898 Blocked: 490.668
Philosopher 003: Think: 4.395 Eat: 0.000 Blocked: 495.605
Philosopher 004: Think: 4.559 Eat: 4.043 Blocked: 491.398
UNIX>
The progression is pictured below. The important feature is that since the philosopher only
check adjacent philosophers, you have a problem when the front of the queue is not an adjacent
philosopher:
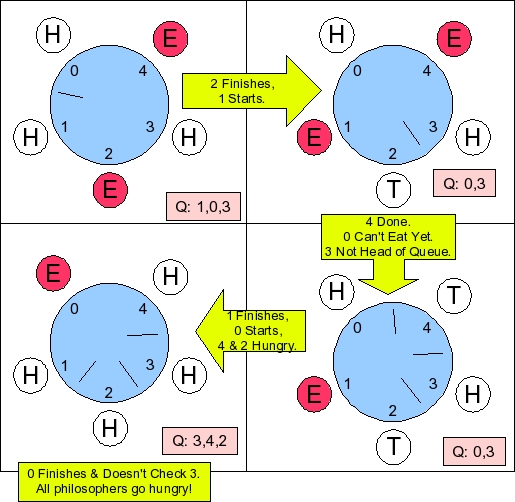 |
Solution #7: Preventing Starvation A Little Better
We can fix this easily by testing the front of the queue instead of testing adjacent philosophers. The fix is in dphil_7.c. First, we write a procedure that tests the front of the queue and wakes up the philosopher:
void test_queue_front(MyPhil *m, Simulation *s)
{
if (dll_empty(m->q)) return;
if (test_philosopher(m->q->flink->val.i, m, s))
cbthread_gsem_V(m->sems[m->q->flink->val.i]);
}
|
Then we call that in i_am_sated() when we put down the chopsticks. It works much better now -- you can see that up until the end of the simulation, the philosophers are still eating:
UNIX> dphil_7 5 3 3 1 10000 10000 4 yes | tail -n 10 9997.746: 000 Putting down stick 001 9998.746: 000 Thinking for 2.559. 9998.746: 001 Picking up stick 001 9999.746: 001 Picking up stick 002 10000.000: Thinktime: 1050.291 Eattime: 1064.865 Blocked_time: 7884.844 Philosopher 000: Think: 1056.339 Eat: 1106.695 Blocked: 7836.965 Philosopher 001: Think: 1027.252 Eat: 1051.870 Blocked: 7920.878 Philosopher 002: Think: 1095.661 Eat: 1110.493 Blocked: 7793.846 Philosopher 003: Think: 987.161 Eat: 1015.708 Blocked: 7997.131 Philosopher 004: Think: 1085.040 Eat: 1039.560 Blocked: 7875.400 UNIX>Unfortunately, though, that blocked time is much higher than the previous solutions. One reason as that we're still not waking up philosophers optimally. Take a look at the following scenario:
 |
You see that when philosopher 0 finishes, she wakes up philosopher 1. However, philosopher 3 is on the queue with chopsticks available, and no one wakes him up. That's inefficient.
Solution #8: Getting the central queue working correctly
The fix is in dphil_8.c. That is to also check the queue right after a philosopher dequeues himself -- this is in am_i_hungry():
if (test_philosopher(p->id, m, p->s)) {
dll_delete_node(m->q->flink);
m->sticks_free[s1] = 0;
m->sticks_free[s2] = 0;
m->my_pstates[p->id] = GOT_STICK_1;
test_queue_front(m, p->s);
pick_up_stick(p, s1, i_am_hungry);
|
The result is less block time:
UNIX> dphil_8 5 3 3 1 10000 10000 4 no | head -n 1 10000.000: Thinktime: 1353.271 Eattime: 1344.127 Blocked_time: 7302.602 UNIX>
Solution #9: Central queues are inefficient
When the table gets large, a central queue seems really inefficient, doesn't it? Suppose that the table size is 100, all philosophers are hungry, philosopher 0 is eating and philosopher 1 is at the head of the queue. Then there are 49 philosophers that can eat, but none will be able to until philosopher 0 is done.For example:
UNIX> dphil_5 101 3 3 1 10000 10000 4 no | head -n 1 10000.000: Thinktime: 1875.589 Eattime: 1881.816 Blocked_time: 6242.595 UNIX> dphil_8 101 3 3 1 10000 10000 4 no | head -n 1 10000.000: Thinktime: 484.010 Eattime: 485.673 Blocked_time: 9030.317 UNIX>That's a big diference, which will be further exacerbated when eat times become large:
UNIX> dphil_5 101 3 30 1 10000 10000 4 no | head -n 1 10000.000: Thinktime: 384.886 Eattime: 3819.452 Blocked_time: 5795.662 UNIX> dphil_8 101 3 30 1 10000 10000 4 no | head -n 1 10000.000: Thinktime: 82.794 Eattime: 791.296 Blocked_time: 9125.910 UNIX>So, can we prevent starvation without a central queue? Sure -- one way is to have each philosopher keep track of what time they became hungry. Then a philosopher can only eat when the chopsticks are available and neither neighbor has been hungry for a longer period of time.
The code is in dphil_9.c. The only changes are that we've added a hunger_time array to MyPhil, and our test_philosopher() routine now tests adjacent philosophers instead of a central queue:
typedef struct {
cbthread_gsem *sems;
int *sticks_free;
int *my_pstates;
double *hunger_time;
} MyPhil;
int test_philosopher(int pid, MyPhil *m, Simulation *s)
{
int before, after;
/* If I'm not wanting the sticks, return false. */
if (m->my_pstates[pid] != WANTING_STICKS) return 0;
/* If the sticks aren't available, return false. */
after = (pid + 1) % s->nphil;
if (!m->sticks_free[pid] || !m->sticks_free[after]) return 0;
/* If the philosopher after me has been waiting longer, return false. */
if (m->my_pstates[after] == WANTING_STICKS &&
m->hunger_time[pid] > m->hunger_time[after]) return 0;
/* If the philosopher before me has been waiting longer, return false. */
before = (pid + s->nphil - 1) % s->nphil;
if (m->my_pstates[before] == WANTING_STICKS &&
m->hunger_time[pid] > m->hunger_time[before]) return 0;
/* Otherwise, all's good! */
return 1;
}
|
We call test_philosopher() when a philosopher is first hungry, and on adjacent philosophers when we put down the sticks.
Interestingly, at a five person table, it performs worse than the central queue:
UNIX> dphil_8 5 3 3 1 10000 10000 4 no | head -n 1 10000.000: Thinktime: 1353.271 Eattime: 1344.127 Blocked_time: 7302.602 UNIX> dphil_9 5 3 3 1 10000 10000 4 no | head -n 1 10000.000: Thinktime: 1193.014 Eattime: 1218.905 Blocked_time: 7588.081 UNIX>However, it does at a 101 person table, although it's still not as good as the non-starvation-preventing solution:
UNIX> dphil_5 101 3 30 1 10000 10000 4 no | head -n 1 10000.000: Thinktime: 384.886 Eattime: 3819.452 Blocked_time: 5795.662 UNIX> dphil_8 101 3 30 1 10000 10000 4 no | head -n 1 10000.000: Thinktime: 82.794 Eattime: 791.296 Blocked_time: 9125.910 UNIX> dphil_9 101 3 30 1 10000 10000 4 no | head -n 1 10000.000: Thinktime: 301.133 Eattime: 3010.205 Blocked_time: 6688.663 UNIX>Why would it perform worse on a 5-person table? For a hint, take a look at the scenario below -- hunger times are next to the philosophers:
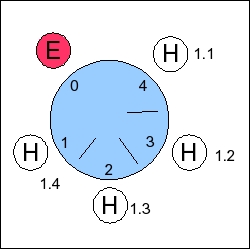 |
That's no better than a central queue, is it? And with a table that small, you are very likely to have situations like the above.
Solution #A: Loosening the hunger time requirement
We can fix the above by loosening the restriction. How about we set a threshold, and you only block if the difference between your hunger time and your neighbor's is above that threshold. Then you still prevent starvation, but you won't have as much blocking.This is in dphil_a.c, and is a two-line fix to test_philosopher(), where we use a threshold of eatavg * 5.
int test_philosopher(int pid, MyPhil *m, Simulation *s)
{
int before, after;
if (m->my_pstates[pid] != WANTING_STICKS) return 0;
after = (pid + 1) % s->nphil;
if (!m->sticks_free[pid] || !m->sticks_free[after]) return 0;
if (m->my_pstates[after] == WANTING_STICKS &&
m->hunger_time[pid] - s->eatavg * 10 > m->hunger_time[after]) return 0;
before = (pid + s->nphil - 1) % s->nphil;
if (m->my_pstates[before] == WANTING_STICKS &&
m->hunger_time[pid] - s->eatavg * 10 > m->hunger_time[before]) return 0;
return 1;
}
|
Now, the performance is back to the level of the solution which allows starvation:
UNIX> dphil_a 5 3 3 1 10000 10000 4 no | head -n 1 10000.000: Thinktime: 1831.361 Eattime: 1838.134 Blocked_time: 6330.505 UNIX> dphil_a 101 3 30 1 10000 10000 4 no | head -n 1 10000.000: Thinktime: 385.485 Eattime: 3806.771 Blocked_time: 5807.745 UNIX>
Solution #B: One last inefficiency
You'll note that solution 4 -- the unfair and asymmetric one -- significantly outperforms the others on the small table:UNIX> dphil_4 5 3 3 1 10000 10000 4 no | head -n 1 10000.000: Thinktime: 1996.924 Eattime: 1954.487 Blocked_time: 6048.589 UNIX>Why? The answer is that all of the solutions from #5 on don't start picking up chopsticks until both are available. Now, suppose your left chopstick is available and the philosopher on your right is putting down his left chopstick. You can improve matters by starting to pick up your left chopstick now instead of waiting until your right chopstick is available.
This is done in dphil_b.c. It's a little tricky, because you have to worry about things that can happen when two philosophers wake up at the same time (which happens quite a bit as it turns out). I'm not going to put the code here, but I represent the state of each chopstick as FREE, USING, ALLOCATED or DROPPING. They are all pretty obvious except for ALLOCATED -- this means that you are picking up the other chopstick and this chopstick is not in use, but you are going to use it.
Now test_philosopher() has more things to worry about -- if either of your sticks are USING or ALLOCATED, then you must block. If both sticks are DROPPING you also must block. Otherwise, you can pick up a stick. I return the number of free sticks:
int test_philosopher(int pid, MyPhil *m, Simulation *s)
{
int before, after;
if (m->my_pstates[pid] != WANTING_STICKS) return 0;
after = (pid + 1) % s->nphil;
if (m->my_pstates[after] == WANTING_STICKS &&
m->hunger_time[pid] - s->eatavg * 10 > m->hunger_time[after]) return 0;
before = (pid + s->nphil - 1) % s->nphil;
if (m->my_pstates[before] == WANTING_STICKS &&
m->hunger_time[pid] - s->eatavg * 10 > m->hunger_time[before]) return 0;
if (m->stick_states[pid] == USING || m->stick_states[after] == USING) return 0;
if (m->stick_states[pid] == ALLOCATED || m->stick_states[after] == ALLOCATED) return 0;
if (m->stick_states[pid] == DROPPING && m->stick_states[after] == DROPPING) return 0;
if (m->stick_states[pid] == DROPPING || m->stick_states[after] == DROPPING) return 1;
return 2;
}
|
I'll leave it up to the interested student to figure out the rest of the code.
Now, performance is the best of all solutions.
UNIX> dphil_b 5 3 3 1 10000 10000 4 no | head -n 1 10000.000: Thinktime: 2080.247 Eattime: 2107.329 Blocked_time: 5812.424 UNIX> dphil_b 101 3 30 1 10000 10000 4 no | head -n 1 10000.000: Thinktime: 390.507 Eattime: 3879.149 Blocked_time: 5730.344 UNIX>
Solution #C: I can't help myself...
You can make the last solution even more efficient if you are judicious about the order in which you put down your chopsticks. If putting down one chopstick will enable a philosopher to start picking up the other chopstick, then put that chopstick down first. This improves performance even more:UNIX> dphil_c 5 3 3 1 10000 10000 4 no | head -n 1 10000.000: Thinktime: 2144.681 Eattime: 2166.637 Blocked_time: 5688.682 UNIX> dphil_c 101 3 30 1 10000 10000 4 no | head -n 1 10000.000: Thinktime: 389.649 Eattime: 3888.602 Blocked_time: 5721.750 UNIX>
In Summary
Here are some graphs to compare the various methodologies. The graphs that I present plot averages of ten runs with different seeds, where each duration is 100,000 seconds. I plot the percentage of time that each philosopher is blocked as a function of the table size (number of philosophers):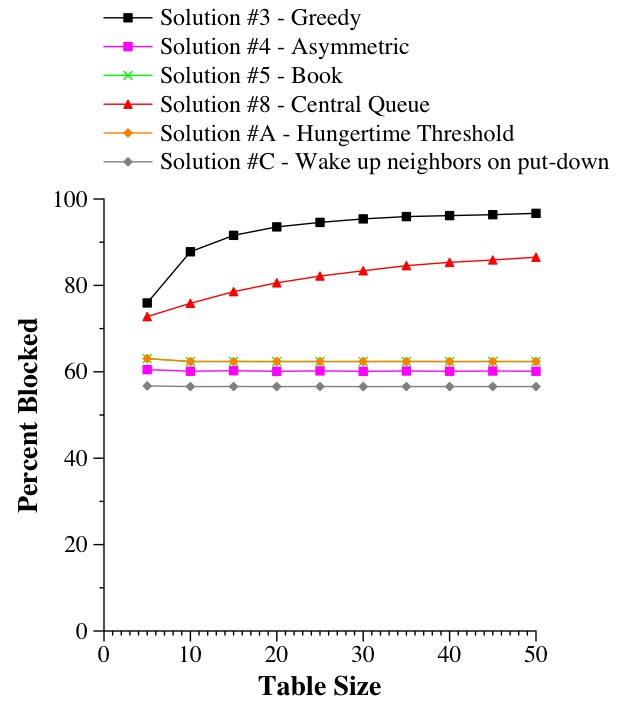 |
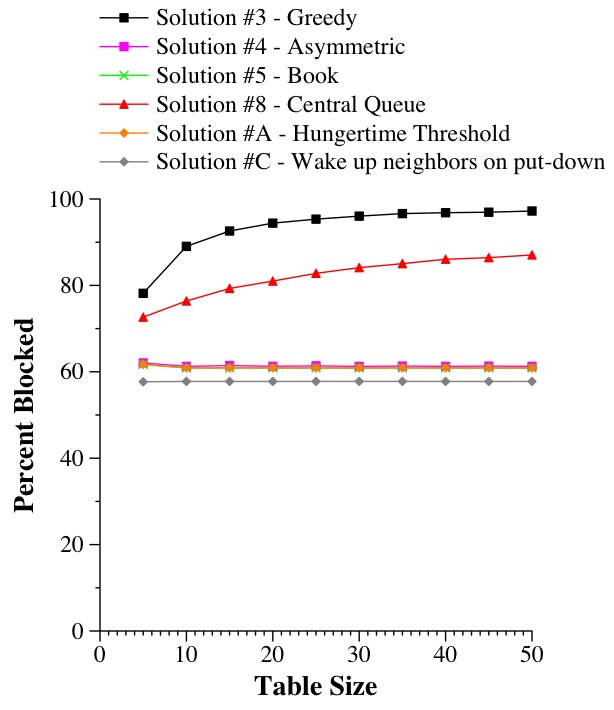 |
These first two simulations are similar. Both represent states where there is always contention for the chopsticks. In each case, the greedy solution is the worst, as you get lots of philosophers holding a chopstick and waiting. The second worst algorithm is the central queue, which as noted above gets worse as the table gets bigger.
The remainder of the algorithms don't appear to depend on the table size. In the first case, where the thinking and eating times are similar, the asymmetric algorithm works better than all but the last, because it doesn't make the philosophers wait until both chopstricks are free before picking a chopstick up.
Below, we show some more examples:
 |
 |
What's going on with the Greedy Solution when the table size is 5? Think about it before looking at the answer.
What's happening is that in nine of the ten cases, the philosophers deadlock! In the first two sets of tests, they don't. Is that intuitive or counter-intuitive? I think the latter -- If you're thinking more, you're less likely to have contention and therefore you're less likely to deadlock.
But that's not the case. In the first two examples, the philosophers are usually hungry or eating. When they're hungry, they are usually blocked waiting for adjacent philosophers to finish, and it is rare for adjacent philosophers to get hungry at the same time. In other words, the contention makes the philosophers eat in a rough pattern, and that pattern prevents deadlock.
When the thinking time is larger, the philosophers are less likely to contend with each other, so they don't get into this pattern of alternating eating. Instead, each starts at a random time. If you choose these random times enough, you are more likely to get that combination where all the philosophers get hungry within a second of each other. Odd, but true. When there are 10 philosophers, that probability is simply too low.
When we remove the sticktime from the equation, solutions 5, A and C all become equivalent.