
I finally made this one, and used the same gluing strategy as the rhombicosidodecahedron (only using an icosidodecahedron and some octahedrons as the gluing substeps).
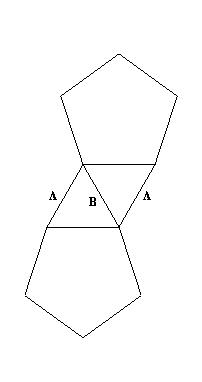
There are two types of tr--tr edge --- those of type A and those of type B (see the figure below). Consider the A edges in pairs as in the Figure. There are 30 such pairs that are analagous to edges of a dodecahedron (or icosahedron). Color these pairs in the same was as you color a dodecahedron that has no two adjacent edges of the same color. Color the B edges so that no two adjacent triangle edges have the same color. You can do this with three colors -- draw out a plan first. This makes a symmetrical coloring that is beautiful. It appears I never took a good picture of the one I made -- pity, as it was gorgeous (I used purple for the pentagons, and three shades of red/pink for the triangles.) Like much of my origami, it was destroyed in one of my moves. That, or it's in my office somewhere... I'll include the bad picture of it below.

