 |
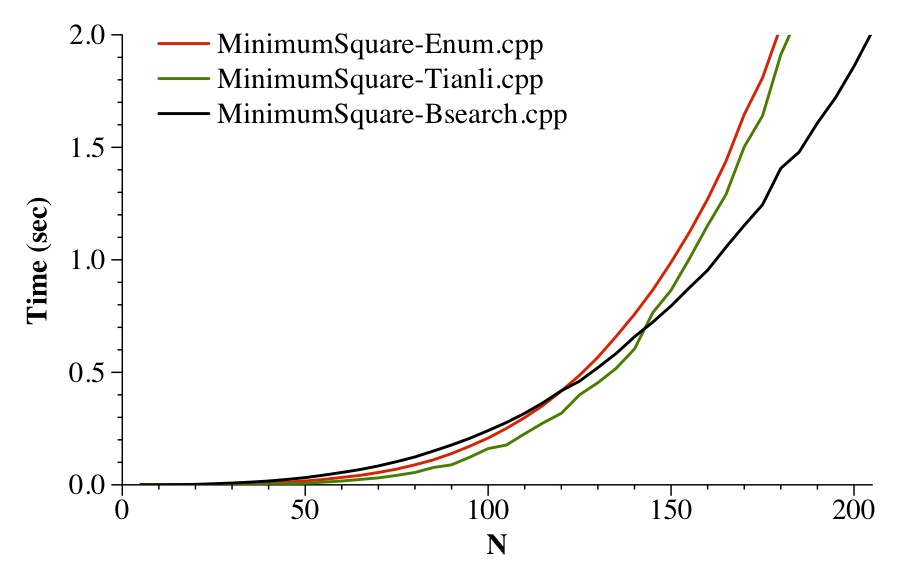
This is an interesting problem, because a brain-dead O(N4) solution is fast enough for Topcoder. I'm sure that's why they made this a D1/250-pointer. However, there are faster solutions. First, there's a very nice O(N3log(N)) solution, but it feels as though you should be able to make it faster than that. And you can. Using binary search and some smart data organization, you can get it down to O(N2log(N)2), which feels much better.
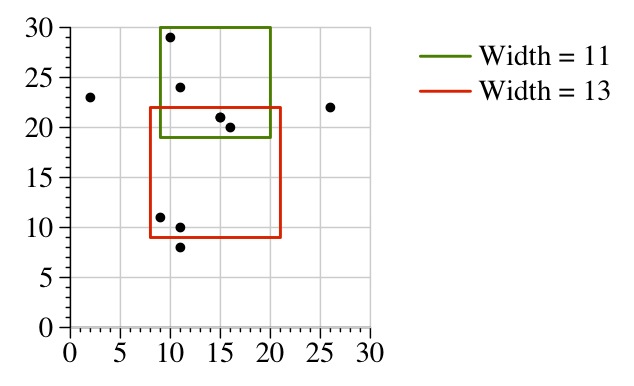
First, read the problem description. Let's give a motivating example, which I have put into my main() as Example 5. Here, the points are:
 |
As with most Topcoder solutions, I spent about a minute trying to be smart, and then I resorted to being stupid. First, it's easier to find the minimum square where the points are allowed to touch the sides. Then add two to the width. Here's the graph with those solutions:
 |
Now, to craft a solution: It should be clear that the bottom-left corner of any solution will have the x value of some point in x and a y value of a point in y. It doesn't have to be the same point. For example, the green square above has a bottom-left point of (10,20), corresponding to the points (10,29) and (16,20). Let's call the bottom-left point (l,b). It should also be clear that if the width of the square is w, then there will be a point whose x value is l+w, or there will be a point whose y value is b+w. That is because there has to be a point on the top or right side of the square. That gives us the brain-dead enumeration:
Here's an example. When l=9 and b=10, the sorted vector will be:
The point at index 3 is 11, which is indeed the minimum width square! It should be pretty clear that making the vector and sorting it is O(N log(N)), which, when combined with the O(N2) of the first two loops makes O(N3log(N)).
| Given l, b and w, how many points fit into the square? |
To do that, we need some data structures. First, we need two maps:
 |
Calculating this matrix is non-trivial -- I'll say how we do that later.
We can use Pts_In_Rect as follows. Our goal is to find the number of points in the square of width w whose bottem-left corner is (l,b). Suppose that our l and b correspond to row r and column c of the matrices. We can use upper_bound() on XV to find c', the column that corresponds to the largest value of x that is less than or equal to l+w. We do this by calling xit = XV.upper_bound(l+w), and then using (xit->second-1). We can do the same thing using YV to find r', the row that corresponds to the largest value of y that is less than or equal to b+w. Then, our number of points can be found with:
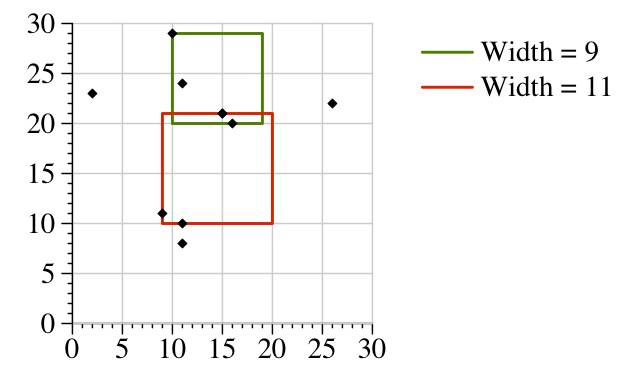
Let's illustrate this with a concrete example. Let's find the number of points in the square with (l,b) equal to (15,21) and a width of 11. As you can see from the picture below, the answer is two:
 |
Now, in this example, r is 5 (corresponding to y=21). So, r+w is 32. If we call YV.upper_bound(21) it will return an iterator to ∞, whose second is 10. Therefore, r' equals 9, corresponding to a y value of 29. This is indeed the largest value of y less than or equal to y+w.
Doing the same for c: c is also 5, corresponding to an x value of 15. If we call XV.upper_bound(26) it will also return an iterator to ∞, whose second is 8. Therefore, c' equals 7, corresponding to an x value of 26. Perfect.
Let's now take a look at the four rectangles in the equation above:
 |
 |
 |
 |
| Pts_In_Rect[r'=9][c'=7] = 9. | Pts_In_Rect[r'=9][c-1=4] = 6. | Pts_In_Rect[r-1=4][c'=7] = 4. | Pts_In_Rect[r-1=4][c-1=4] = 3. |
The answer is (9-6-4+3) = 2. Yay! Putting it all together. Given (l,b), we can now perform a binary search on w to determine the smallest value of w which contains at least K points. We can start the search with a low value of zero, and a high value which is the maximum possible value of w. That will converge in log(high) steps. Of course, high may be a lot greater than N (2,000,000,000, given the constraints), so if you want to make this log(N), you'll have to do something fancy with indices rather than values of w. I'm not going to do that when I code it up, though, because log(high) is going to max out at 31. It's not worth my time.
 Step 1: Allocate Pts_In_Rect and set all the entries to zero. This is O(N2). |
 Step 2: Set each point's entry in Pts_In_Rect to one. This is O(N). |
 Step 3: Iterate from left to right -- set each column's entry to the sum of it and the entry to the left. At the end, every element in Pts_In_Rect[r][c] contains the number of points with y equal to YV_V[r] and x less than or equal to XV_V[c]. This is O(N2). |
 Step 4: Iterate from top to bottom -- set each row's entry to the sum of it and the entry above it. This sets Pts_In_Rect to what we want. This is also O(N2). |
 |
class MinimumSquare {
public:
long long minArea(vector <int> x, vector <int> y, int k);
vector<long long> XV_V; // The unique X values in order, sentinelized on both sides.
vector<long long> YV_V; // The unique Y values in order, sentinelized on both sides.
map <long long, long long> XV; // Values in XV_V. XV[XV[i]] = i.
map <long long, long long> YV; // Values in YV_V. YV[YV[i]] = i.
vector < vector <long long> > Pts_In_Rect; // Pts_In_Rect[i][j] stores the number of points
// whose x values are <= XV_V[j] and
// whose y values are <= YV_V[i].
long long Maxwidth; // Maximum width of a square, over all points.
long long K; // Target number of points.
/* Pts_In_Square() returns the number of points in the square with the given width, whose
lower left-hand corner is ( XV_V[xindex], YV_V[yindex] ). It is O(log(n)). */
long long Pts_In_Square(int xindex, int yindex, long long width);
/* Do_Binary_Search() does a binary search over all widths to
find the smallest one that has at least K points when its lower
left-hand corner is ( XV_V[xindex], YV_V[yindex] ). If there is no
such width, it will return (Maxwidth+1) */
long long Do_Binary_Search(long long xindex, long long yindex);
};
|
Now, we'll walk through the code in minArea. Here's the code to create XV, YV, XV_V and YV_V. Note that we simply use long long's for everything, and we sentinelize as follows. The low sentinel is the minimum value minus one. The high sentinel is a giant long long that is way bigger than any legal value:
long long MinimumSquare::minArea(vector <int> x, vector <int> y, int k)
{
map <long long, long long>::iterator xit, yit;
long long i, j, w, row, col, min, bestw, mw;
K = k;
/* Insert the unique X and Y values into XV and YV respectively.
Give them values of zero. */
for (i = 0; i < x.size(); i++) {
XV[x[i]] = 0;
YV[y[i]] = 0;
}
/* Calculate the maximum possible width of a square. */
i = XV.rbegin()->first - XV.begin()->first;
j = YV.rbegin()->first - YV.begin()->first;
Maxwidth = (i > j) ? i : j;
/* Sentinelize them, so that there is a minimum value in each map that
doesn't correspond to any point, and so that there is a maximum value
that will be bigger than any possible maximum value. */
min = XV.begin()->first;
XV[min-1] = 0;
XV[0xffffffffffffLL] = 0;
min = YV.begin()->first;
YV[min-1] = 0;
YV[0xffffffffffffLL] = 0;
/* Now create the vals, so that the i'th entry in each map has an val of i; */
i = 0;
for (xit = XV.begin(); xit != XV.end(); xit++) {
xit->second = i;
i++;
}
i = 0;
for (yit = YV.begin(); yit != YV.end(); yit++) {
yit->second = i;
i++;
}
/* Create vectors XV_V and YV_V, which have the keys from XV and YV, respectively.
You'll note that XV[XV_V[i]] equals i, and YV[YV_V[i]] equals i. */
for (xit = XV.begin(); xit != XV.end(); xit++) XV_V.push_back(xit->first);
for (yit = YV.begin(); yit != YV.end(); yit++) YV_V.push_back(yit->first);
/* Error check */
// for (i = 0; i < XV_V.size(); i++) printf(" %d", XV_V[i]); printf("\n");
// for (i = 0; i < YV_V.size(); i++) printf(" %d", YV_V[i]); printf("\n");
|
Next is the code to create Pts_In_Rect -- it follows the four steps outlined above:
/* Create the matrix Pts_In_Rect. This is a four-step activity.
1. Allocate the matrix and put all zeros into it.
2. For every point in the problem, set its entry in Pts_In_Rect to 1.
3. For every element (i,j) in the matrix with i and j > 0, set the element to
the sum of its value and the value in the column to the left of it.
At the end of this step, Pts_In_Rect[i][j] contains the number of points
in row i whose x values are <= XV[j].
4. Lastly for every element (i,j) in the matrix with i and j > 0, set the
element to the sum of its value and the value in the row above it.
Now, Pts_In_Rect[i][j] contains what we want -- the number of points whose
x values are <= XV[j] and whose y values are <= YV[i]. */
/* Step 1 */
Pts_In_Rect.resize(YV_V.size());
for (i = 0; i < Pts_In_Rect.size(); i++) {
Pts_In_Rect[i].resize(XV_V.size(), 0);
}
/* Step 2 */
for (i = 0; i < x.size(); i++) {
col = XV[x[i]];
row = YV[y[i]];
Pts_In_Rect[row][col] = 1;
}
/* Step 3 */
for (i = 1; i < Pts_In_Rect.size(); i++) {
for (j = 1; j < Pts_In_Rect[i].size(); j++) {
Pts_In_Rect[i][j] += (Pts_In_Rect[i][j-1]);
}
}
/* Step 3 */
for (j = 1; j < Pts_In_Rect[0].size(); j++) {
for (i = 1; i < Pts_In_Rect.size(); i++) {
Pts_In_Rect[i][j] += (Pts_In_Rect[i-1][j]);
}
}
/* Error check -- print out the values. */
/*
for (i = 0; i < Pts_In_Rect.size(); i++) {
for (j = 0; j < Pts_In_Rect[i].size(); j++) printf(" %2lld", Pts_In_Rect[i][j]);
printf("\n");
} */
|
And finally, enumerate through each potential lower-left corner, and do a binary search on w. Store the smallest value of w. At the end, add two and return the square, since the problem asks for the area:
/* Now, for each x value, and each y value, do a binary search starting with
a low width of 0 and a high width of maxwidth, and find the smallest value
of w such that Pts_In_Square(x,y,w) >= K. */
bestw = Maxwidth;
for (i = 1; i < XV.size()-1; i++) {
for (j = 1; j < YV.size()-1; j++) {
mw = Do_Binary_Search(i, j);
if (mw < bestw) bestw = mw;
}
}
/* Add two, because the problem wants squares where the points aren't on the
borders of the square, and we calculated squares where the points are on
border. */
bestw += 2;
return (bestw * bestw);
}
|
Here's the code for the binary search. The commenting explains how it works:
/* The binary search. Starts with low = 0, and high = Maxwidth. Your invariant
will be that Pts_In_Square(xindex, yindex, low) is < K, and
Pts_In_Square(xindex, yindex, high) is >= K.
If either of these if false to start with, you can return. Otherwise, you keep
checking the middle of low and high, and then updating low or high accordingly.
You stop when low = high-1, and you return high, because that is the smallest
width that has enough points in it. */
long long MinimumSquare::Do_Binary_Search(long long xindex, long long yindex)
{
long long low, mid, high;
low = 0;
high = Maxwidth;
if (Pts_In_Square(xindex, yindex, high) < K) return Maxwidth+1;
if (Pts_In_Square(xindex, yindex, low) >= K) return low;
while (1) {
if (high == low + 1) return high;
mid = (high + low) / 2;
if (Pts_In_Square(xindex, yindex, mid) >= K) {
high = mid;
} else {
low = mid;
}
}
return -1;
}
|
And finally, here's the code to find the number of points in the square with a given lower-left corner and a given width:
/* Best to look at the lecture notes for this one -- you use upper_bound() to
find the high x and y points. The fact that you have sentinelize this helps,
because you know that upper_bound will always return a legal iterator.
Then use the equation of four values involving Pts_In_Rect. */
long long MinimumSquare::Pts_In_Square(int xindex, int yindex, long long width)
{
map <long long, long long>::iterator xit;
map <long long, long long>::iterator yit;
int xh, yh;
long long x, y;
x = XV_V[xindex];
y = YV_V[yindex];
xit = XV.upper_bound(x+width);
xh = xit->second-1;
yit = YV.upper_bound(y+width);
yh = yit->second-1;
return Pts_In_Rect[yh][xh] - Pts_In_Rect[yh][xindex-1]
- Pts_In_Rect[yindex-1][xh]
+ Pts_In_Rect[yindex-1][xindex-1];
}
|