 |
Example 0:
{"single","round","match"}
Returns: "Possible"
One possible ordering of the letters is: "bfjkmapqrositchundglevwxyz".
Example 1:
{"topcoder","topcoder"}
Returns: "Impossible"
The word "topcoder" can never be a good word. The character 'o' cannot be both before 'p' and after 'p'.
Example 2:
{"algorithm", "contest"}
Returns: "Impossible"
Example 3:
{"pink","floyd"}
Returns: "Possible"
Example 4:
{"gimnasia","y","esgrima","la","plata"}
Returns: "Impossible"
Example 5:
{"hello","hello"}
Returns: "Possible"
This is a good word for any ordering of the letters in which 'h', 'e', 'l', and 'o' appear in this order.
Example 6:
{"abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"}
Returns: "Possible"
In this case the English alphabet is a valid ordering.
Example 7:
{"abc","bca"}
Returns: "Impossible"
'a' must come before 'c' (because of the first word) and after 'c' (because of the second word) and that is a contradiction.
Example 8:
{"aaaaa","eeeee","iiiii","ooooo","uuuuu"}
Returns: "Possible"
Any order is valid in this case
Example 9:
{"ab","bc","ca"}
Returns: "Impossible"
How does that help you? Well, if you create the graph, and do a topological sort on it, and it completes, then you have found a valid orer, and it's "Possible". If you do the topological sort and it can't complete, that's because the graph has a cycle. You can then return "Impossible".
I have commented code for this -- you can see it with colored comments here.
If this were an undirected graph, then all you need is a visited array, which is a boolean. See the section entitled "Depth First Search To Perform Cycle Detection", from the DFS lecture notes from CS302 for a nice example.
In a directed graph, it's a little trickier. The reason is that in an undirected graph, if there is a path from A to B, then there is a path from B to A. That is not true in a directed graph.
What I do to handle the directed graph is make visited an integer, which can hold one of three values:
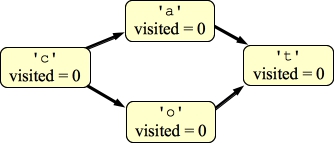
 |
You'll note that this graph has no cycles. Were it undirected, it would have a cycle. Now, suppose you run through the letters in order to detect cycles. You start with 'a'. When you call DFS on it, you set visited to one, and you will then call DFS on 't':
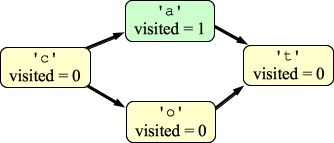 |
This will set t's visited field to one, and since there are no outgoing edges, the DFS will complete instantly. There is no cycle with 't', so you set its visited field to two, and return to 'a':
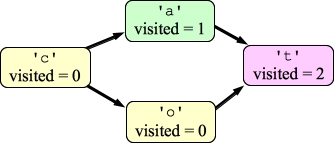 |
Now, 'a' is done. You set its visited field to two, and the DFS returns that there is no cycle with 'a'. Here's the state of the graph:
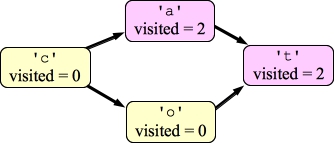 |
Next, you call DFS on 'c'. This sets its visited field to one, and calls DFS on 'a'. Since 'a' has completed its DFS, you return instantly that there is no cycle with 'a'. Here's the state of the graph:
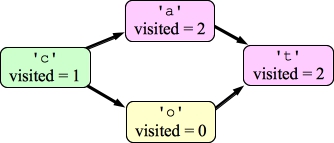 |
Next, you process the edges from 'c' to 'o', and call DFS on 'o'. This will set o's visited field to one, and it will call DFS on 't':
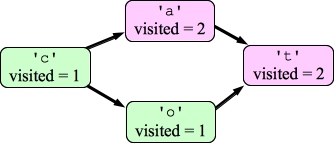 |
Since 't' has completed its DFS, you return instantly that there is no cycle with 't'. Now, 'o' can return that there is no cycle, as can 'c':
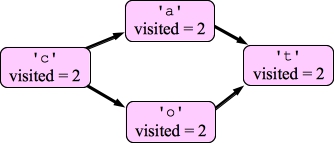 |
You will call DFS on 'o' and 't' next, but they are already done. Now, you're done and can return "Possible", because there are no cycles in the graph.
I have commented code for this too -- you can see it with colored comments here.