





 |
 |
 |
 |
 |
 |
 |
By now we have seen several examples of composition (the ability to combine language features in a variety of arrangements). One of the first examples we saw was using a function invocation as part of an expression. Another example is the nested structure of statements: you can put an if statement within a while loop, or within another if statement, etc.
Having seen this pattern, and having learned about vectors and objects, you should not be surprised to learn that you can have vectors of objects. In fact, you can also have objects that contain vectors (as instance variables); you can have vectors that contain vectors; you can have objects that contain objects, and so on.
In the next two chapters we will look at some examples of these combinations, using Card objects as a case study.
If you are not familiar with common playing cards, now would be a good time to get a deck, or else this chapter might not make much sense. There are 52 cards in a deck, each of which belongs to one of four suits and one of 13 ranks. The suits are Spades, Hearts, Diamonds and Clubs (in descending order in Bridge). The ranks are Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen and King. Depending on what game you are playing, the rank of the Ace may be higher than King or lower than 2.
If we want to define a new object to represent a playing card, it is pretty obvious what the instance variables should be: rank and suit. It is not as obvious what type the instance variables should be. One possibility is strings, containing things like "Spade" for suits and "Queen" for ranks. One problem with this implementation is that it would not be easy to compare cards to see which had higher rank or suit.
An alternative is to use integers to encode the ranks and suits. By "encode," I do not mean what some people think, which is to encrypt, or translate into a secret code. What a computer scientist means by "encode" is something like "define a mapping between a sequence of numbers and the things I want to represent." For example,
| Spades | -> | 3 |
| Hearts | -> | 2 |
| Diamonds | -> | 1 |
| Clubs | -> | 0 |
The symbol -> is mathematical notation for "maps to." The obvious feature of this mapping is that the suits map to integers in order, so we can compare suits by comparing integers. The mapping for ranks is fairly obvious; each of the numerical ranks maps to the corresponding integer, and for face cards:
| Jack | -> | 11 |
| Queen | -> | 12 |
| King | -> | 13 |
The reason I am using mathematical notation for these mappings is that they are not part of the C++ program. They are part of the program design, but they never appear explicitly in the code. The class definition for the Card type looks like this:
struct CardThere are two constructors for Cards. You can tell that they are constructors because they have no return type and their name is the same as the name of the structure. The first constructor takes no arguments and initializes the instance variables to a useless value (the zero of clubs).
The second constructor is more useful. It takes two parameters, the suit and rank of the card.
The following code creates an object named threeOfClubs that represents the 3 of Clubs:
Card threeOfClubs (0, 3);The first argument, 0 represents the suit Clubs, the second, naturally, represents the rank 3.
When you create a new type, the first step is usually to declare the instance variables and write constructors. The second step is often to write a function that prints the object in human-readable form.
In the case of Card objects, "human-readable" means that we have to map the internal representation of the rank and suit onto words. A natural way to do that is with a vector of strings. You can create a vector of strings the same way you create an vector of other types:
vector<string> suits (4);Of course, in order to use vectors and strings, you will have to include the header files for both.
To initialize the elements of the vector, we can use a series of assignment statements.
suits[0] = "Clubs";A state diagram for this vector looks like this:

We can build a similar vector to decode the ranks. Then we can select the appropriate elements using the suit and rank as indices. Finally, we can write a function called print that outputs the card on which it is invoked:
void Card::print () constThe expression suits[suit] means "use the instance variable suit from the current object as an index into the vector named suits, and select the appropriate string."
Because print is a Card member function, it can refer to the instance variables of the current object implicitly (without having to use dot notation to specify the object). The output of this code
Card card (1, 11);is Jack of Diamonds.
You might notice that we are not using the zeroeth element of the ranks vector. That's because the only valid ranks are 1–13. By leaving an unused element at the beginning of the vector, we get an encoding where 2 maps to "2", 3 maps to "3", etc. From the point of view of the user, it doesn't matter what the encoding is, since all input and output uses human-readable formats. On the other hand, it is often helpful for the programmer if the mappings are easy to remember.
In order for two cards to be equal, they have to have the same rank and the same suit. Unfortunately, the == operator does not work for user-defined types like Card, so we have to write a function that compares two cards. We'll call it equals. It is also possible to write a new definition for the == operator, but we will not cover that in this book.
It is clear that the return value from equals should be a boolean that indicates whether the cards are the same. It is also clear that there have to be two Cards as parameters. But we have one more choice: should equals be a member function or a free-standing function?
As a member function, it looks like this:
bool Card::equals (const Card& c2) constTo use this function, we have to invoke it on one of the cards and pass the other as an argument:
Card card1 (1, 11);This method of invocation always seems strange to me when the function is something like equals, in which the two arguments are symmetric. What I mean by symmetric is that it does not matter whether I ask "Is A equal to B?" or "Is B equal to A?" In this case, I think it looks better to rewrite equals as a nonmember function:
bool equals (const Card& c1, const Card& c2)When we call this version of the function, the arguments appear side-by-side in a way that makes more logical sense, to me at least.
if (equals (card1, card2)) {Of course, this is a matter of taste. My point here is that you should be comfortable writing both member and nonmember functions, so that you can choose the interface that works best depending on the circumstance.
For basic types like int and double, there are comparison operators that compare values and determine when one is greater or less than another. These operators (< and > and the others) don't work for user-defined types. Just as we did for the == operator, we will write a comparison function that plays the role of the > operator. Later, we will use this function to sort a deck of cards.
Some sets are totally ordered, which means that you can compare any two elements and tell which is bigger. For example, the integers and the floating-point numbers are totally ordered. Some sets are unordered, which means that there is no meaningful way to say that one element is bigger than another. For example, the fruits are unordered, which is why we cannot compare apples and oranges. As another example, the bool type is unordered; we cannot say that true is greater than false.
The set of playing cards is partially ordered, which means that sometimes we can compare cards and sometimes not. For example, I know that the 3 of Clubs is higher than the 2 of Clubs because it has higher rank, and the 3 of Diamonds is higher than the 3 of Clubs because it has higher suit. But which is better, the 3 of Clubs or the 2 of Diamonds? One has a higher rank, but the other has a higher suit.
In order to make cards comparable, we have to decide which is more important, rank or suit. To be honest, the choice is completely arbitrary. For the sake of choosing, I will say that suit is more important, because when you buy a new deck of cards, it comes sorted with all the Clubs together, followed by all the Diamonds, and so on.
With that decided, we can write isGreater. Again, the arguments (two Cards) and the return type (boolean) are obvious, and again we have to choose between a member function and a nonmember function. This time, the arguments are not symmetric. It matters whether we want to know "Is A greater than B?" or "Is B greater than A?" Therefore I think it makes more sense to write isGreater as a member function:
bool Card::isGreater (const Card& c2) constThen when we invoke it, it is obvious from the syntax which of the two possible questions we are asking:
Card card1 (2, 11);You can almost read it like English: "If card1 isGreater card2 ..." The output of this program is
Jack of HeartsAccording to isGreater, aces are less than deuces (2s). As an exercise, fix it so that aces are ranked higher than Kings, as they are in most card games.
The reason I chose Cards as the objects for this chapter is that there is an obvious use for a vector of cards—a deck. Here is some code that creates a new deck of 52 cards:
vector<Card> deck (52);Here is the state diagram for this object:
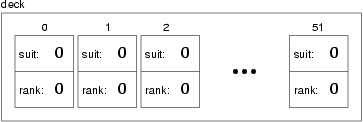
The three dots represent the 48 cards I didn't feel like drawing. Keep in mind that we haven't initialized the instance variables of the cards yet. In some environments, they will get initialized to zero, as shown in the figure, but in others they could contain any possible value.
One way to initialize them would be to pass a Card as a second argument to the constructor:
Card aceOfSpades (3, 1);This code builds a deck with 52 identical cards, like a special deck for a magic trick. Of course, it makes more sense to build a deck with 52 different cards in it. To do that we use a nested loop.
The outer loop enumerates the suits, from 0 to 3. For each suit, the inner loop enumerates the ranks, from 1 to 13. Since the outer loop iterates 4 times, and the inner loop iterates 13 times, the total number of times the body is executed is 52 (13 times 4).
int i = 0;I used the variable i to keep track of where in the deck the next card should go.
Notice that we can compose the syntax for selecting an element from an array (the [] operator) with the syntax for selecting an instance variable from an object (the dot operator). The expression deck[i].suit means "the suit of the ith card in the deck".
As an exercise, encapsulate this deck-building code in a function called buildDeck that takes no parameters and that returns a fully-populated vector of Cards.
Whenever you are working with vectors, it is convenient to have a function that prints the contents of the vector. We have seen the pattern for traversing a vector several times, so the following function should be familiar:
void printDeck (const vector<Card>& deck) {By now it should come as no surprise that we can compose the syntax for vector access with the syntax for invoking a function.
Since deck has type vector<Card>, an element of deck has type Card. Therefore, it is legal to invoke print on deck[i].
The next function I want to write is find, which searches through a vector of Cards to see whether it contains a certain card. It may not be obvious why this function would be useful, but it gives me a chance to demonstrate two ways to go searching for things, a linear search and a bisection search.
Linear search is the more obvious of the two; it involves traversing the deck and comparing each card to the one we are looking for. If we find it we return the index where the card appears. If it is not in the deck, we return –1.
int find (const Card& card, const vector<Card>& deck) {The loop here is exactly the same as the loop in printDeck. In fact, when I wrote the program, I copied it, which saved me from having to write and debug it twice.
Inside the loop, we compare each element of the deck to card. The function returns as soon as it discovers the card, which means that we do not have to traverse the entire deck if we find the card we are looking for. If the loop terminates without finding the card, we know the card is not in the deck and return -1.
To test this function, I wrote the following:
vector<Card> deck = buildDeck ();The output of this code is
I found the card at index = 17If the cards in the deck are not in order, there is no way to search that is faster than the linear search. We have to look at every card, since otherwise there is no way to be certain the card we want is not there.
But when you look for a word in a dictionary, you don't search linearly through every word. The reason is that the words are in alphabetical order. As a result, you probably use an algorithm that is similar to a bisection search:
If you ever get to the point where there are two adjacent words on the page and your word comes between them, you can conclude that your word is not in the dictionary. The only alternative is that your word has been misfiled somewhere, but that contradicts our assumption that the words are in alphabetical order.
In the case of a deck of cards, if we know that the cards are in order, we can write a version of find that is much faster. The best way to write a bisection search is with a recursive function. That's because bisection is naturally recursive.
The trick is to write a function called findBisect that takes two indices as parameters, low and high, indicating the segment of the vector that should be searched (including both low and high).
Steps 3 and 4 look suspiciously like recursive invocations. Here's what this all looks like translated into C++:
int findBisect (const Card& card, const vector<Card>& deck,Although this code contains the kernel of a bisection search, it is still missing a piece. As it is currently written, if the card is not in the deck, it will recurse forever. We need a way to detect this condition and deal with it properly (by returning -1).
The easiest way to tell that your card is not in the deck is if there are no cards in the deck, which is the case if high is less than low. Well, there are still cards in the deck, of course, but what I mean is that there are no cards in the segment of the deck indicated by low and high.
With that line added, the function works correctly:
int findBisect (const Card& card, const vector<Card>& deck,I added an output statement at the beginning so I could watch the sequence of recursive calls and convince myself that it would eventually reach the base case. I tried out the following code:
cout << "I found the card at index = " << findBisect (deck[23], deck, 0, 51) << endl;And got the following output:
0, 51Then I made up a card that is not in the deck (the 15 of Diamonds), and tried to find it. I got the following:
0, 51These tests don't prove that this program is correct. In fact, no amount of testing can prove that a program is correct. On the other hand, by looking at a few cases and examining the code, you might be able to convince yourself.
The number of recursive calls is fairly small, typically 6 or 7. That means we only had to call equals and isGreater 6 or 7 times, compared to up to 52 times if we did a linear search. In general, bisection is much faster than a linear search, especially for large vectors.
Two common errors in recursive programs are forgetting to include a base case and writing the recursive call so that the base case is never reached. Either error will cause an infinite recursion, in which case C++ will (eventually) generate a run-time error.
Looking at the interface to findBisect
int findBisect (const Card& card, const vector<Card>& deck,it might make sense to treat three of the parameters, deck, low and high, as a single parameter that specifies a subdeck.
This kind of thing is quite common, and I sometimes think of it as an abstract parameter. What I mean by "abstract," is something that is not literally part of the program text, but which describes the function of the program at a higher level.
For example, when you call a function and pass a vector and the bounds low and high, there is nothing that prevents the called function from accessing parts of the vector that are out of bounds. So you are not literally sending a subset of the deck; you are really sending the whole deck. But as long as the recipient plays by the rules, it makes sense to think of it, abstractly, as a subdeck.
There is one other example of this kind of abstraction that you might have noticed in Section 9.3, when I referred to an "empty" data structure. The reason I put "empty" in quotation marks was to suggest that it is not literally accurate. All variables have values all the time. When you create them, they are given default values. So there is no such thing as an empty object.
But if the program guarantees that the current value of a variable is never read before it is written, then the current value is irrelevant. Abstractly, it makes sense to think of such a variable as "empty."
This kind of thinking, in which a program comes to take on meaning beyond what is literally encoded, is a very important part of thinking like a computer scientist. Sometimes, the word "abstract" gets used so often and in so many contexts that it is hard to interpret. Nevertheless, abstraction is a central idea in computer science (as well as many other fields).
A more general definition of "abstraction" is "The process of modeling a complex system with a simplified description in order to suppress unnecessary details while capturing relevant behavior."
Revised 2008-12-06.
 |
 |
 |
 |
 |
 |
 |