Paper Solutions
---400---
/ \
-200- 500
/ \ / \
150 325 450 600
/ \ \
50 170 375
/
160
To delete 200 from this tree we must find the largest child in the left
subtree, which is 170, and delete it. We will then replace 200 with 170. 170
has a single child, so to delete 170, we replace 170 with this child, producing
the tree:
---400---
/ \
-200- 500
/ \ / \
150 325 450 600
/ \ \
50 160 375
Then we replace 200 with 170, producing the final result:
---400---
/ \
-170- 500
/ \ / \
150 325 450 600
/ \ \
50 160 375
Incorrect but worth 5 points: The course notes told you to delete the
largest child from the left subtree and replace the deleted key with this
child. If you instead deleted the smallest
child from the right subtree, and replaced the deleted key with this child,
you could get 5 points of partial credit. 325 is the smallest child in the
right subtree, so you first delete 325. Since 325 has a single child, you
replace 325 with 375, and you replace 200 with 325. The final tree in this
case is:
---400---
/ \
-325- 500
/ \ / \
150 375 450 600
/ \
50 170
/
160
-300-
/ \
175 400
/ \
100 250
/ / \
50 200 275
The left rotation will cause 175 to become a left child of 250. In so doing
the left subtree of 250, which is rooted at 200, will become an orphan
because 175 is taking
its place as 250's left child. Therefore 175 adopts 200 as its left child.
175 retains the subtree rooted at 100 as its left child.
Note that it is ok for 175 to adopt 200
as its right subtree because all of the values in 200's tree are greater than 175.
The final tree becomes:
-300-
/ \
250 400
/ \
175 275
/ \
100 200
/
50
--100--
/ \
40 200
/ \ / \
20 60 150 400
/ \
125 175
/
160
- Identify the bottom-most node
that violates the AVL condition and explain why
that node violates the AVL condition.
In the tree below I have labeled each node with its height. Since 200 is the first node whose subtree heights differ by more than 1, it is the first node to violate the AVL condition.
----100(4)-- / \ 40(1) 200(3) / \ / \ (0)20 60(0) (2)150 400(0) / \ (0)125 175(1) / 160(0) - In order to rebalance the tree do we have to use the zig-zig case
or the zig-zag case? Justify your answer.
We must use the zig-zag case. If we follow the route of the path followed for the insertion of 160, we see that we first went left from 200, to 150, and then right, to 175. This left-right traversal is a zig-zag.
- Use the proper rotation(s) to rebalance the above tree so that it
becomes a legitimate AVL tree.
We need to use a double rotation since we have a zig-zag. We will first do a left rotation about the grandchild of 200, which is 175, and then do a right rotation about 175:
Here is the original tree: --100-- / \ 40 200 / \ / \ 20 60 150 400 / \ 125 175 / 160--100--- --100-- left rotation / \ right rotation / \ ------------> 40 200 -------------> 40 175 / \ / \ / \ / \ 20 60 175 400 20 60 150 200 / / \ \ 150 125 160 400 / \ 125 160The left rotation makes 150 be a left child of 175. 160 becomes orphaned in this process and since 150's right child is now freed up, 150 adopts 160 as its right child. The right rotation makes 200 be a right child of 175. This rotation is fairly simple since no orphans are created in the process and therefore no adoptions are required.
Euclid's algorithm is a recursive algorithm for finding the gcd of two integers a and b that can be expressed as follows:
- If a equals b, then the gcd is a
- Otherwise the gcd evenly divides the positive difference between a
and b (|a-b|), and the smaller of a and b.
For example, for 48 and 20:
- gcd(48, 20) reduces to finding the gcd of 28, the difference between 48 and 20, and 20, which is the smaller of 48 and 20.
- gcd(28, 20) reduces to finding the gcd of 8 (28-20) and 20 (lesser of 20 and 28).
- gcd(8, 20) reduces to finding the gcd of 12 (20-8) and 8 (lesser of 8 and 20).
- gcd(12, 8) reduces to finding the gcd of 4 (12-8) and 8 (lesser of 8 and 12).
- gcd(4, 8) reduces to finding the gcd of 4 (8-4) and 4 (lesser of 4 and 8).
- gcd(4, 4) is 4 because 4 equals 4.
- base case: 0! = 1, 1! = 1
- recursive case: n! = n * (n-1)!
- Write the base case for gcd(a,b).
The base case occurs when you are asked to find the gcd of the same two integers:
gcd(a,a) = a or gcd(a, b) = a if a = b
- Write the recursive case(s) for gcd(a,b).
gcd(a, b) = gcd(a - b, b) if a > b gcd(a, b) = gcd(b - a, a) if a < b
int i, j;
int sum = 0;
for (i = 0; i < n; i++)
sum += i;
for (j = 0; j < n/2; j++)
sum *= j;
|
int search(vector<string>names, string target) {
int high = names.size()-1, low=0, mid;
do {
mid = (low + high) / 2;
if (target == names[mid])
return mid;
else if (target < names[mid])
high = mid - 1;
else
low = mid + 1;
} while (low <= high);
return -1;
}
|
|
int i, j;
int sum = 0;
for (i = 0; i < n; i++) {
for (j = 1; j < n; j *= 2) {
sum += a[i][j];
}
}
cout << sum;
|
For each fragment of code, please circle its Big-O running time:
a O(n)--the two O(n) loops are sequential
b O(log n)--the input gets split in two at each step
c O(1)--there are no loops in this code
d O(n log n)--the inner loop iterates log n times and the outer loop
iterates n times
a. array
b. vector
c. stack
d. deque
e. hash table
f. list
g. binary search tree
h. AVL tree
For each of the following questions choose the best answer from the above list. Assume that the size of an array is fixed once it is created, and that its size cannot be changed thereafter. Sometimes it may seem as though two or more choices would be equally good. In those cases think about the operations that the data structures support and choose the data structure whose operations are best suited for the problem. You may have to use the same answer for more than one question:
- AVL tree The data structure you should use if you want to
implement a map using a tree and you want the tree
that will be balanced regardless of whether the
keys are presented in random order or nearly sorted
order.
- hash table The data structure that provides the most efficient
average-case methods for finding, inserting, and deleting keys as long as the keys do not
have to be kept in sorted order.
- vector The data structure you should use if you want to implement
a stack where you insert
or delete elements only at the back of the data structure
and the data structure can become arbitrarily large.
- deque The data structure you should use to store a set of
printing jobs, where new printing jobs should be added
to the back of the queue and jobs to be printed should be removed from
the front of the queue.
- vector The data structure that is used to implement hashing with
linear probing when the size of the data is not known in advance.
- array The data structure you will use for the following histogram-like program. It is going to
take as input a bunch of data points which are integers
and it will count how many of each value there is.
For example, consider the following data points:
( 11, 58, 23, 23, 11, 16, 23 )Our program will report that 11 has two data points, 16 has one data point, 23 has 3 data points, and 58 has one data point. Assume that you know in advance that the data points range in value from 0-100.

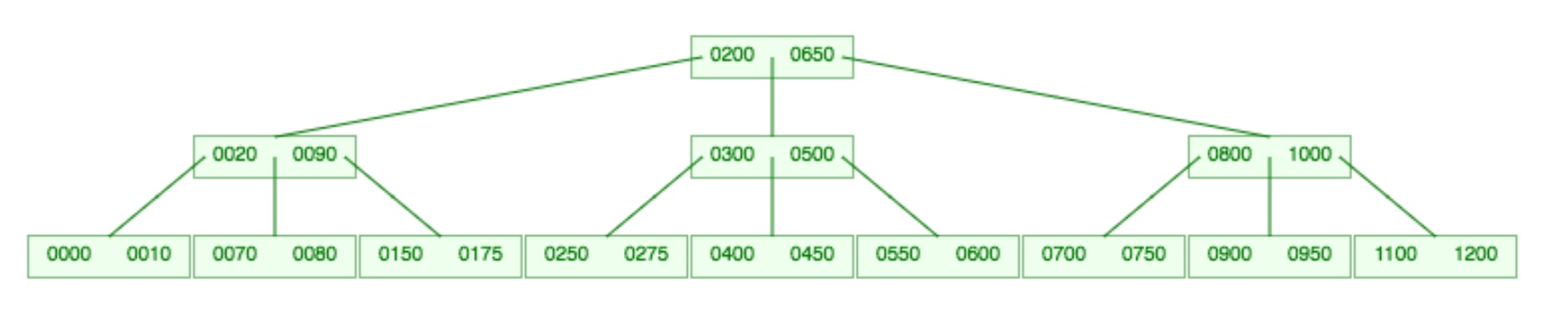
Solution: 700 gets inserted into the leaf node containing the keys 550, 600, 650, and 750. Since the B-tree is of order 5, nodes can hold only 4 keys. Hence we must split the leaf node and promote the middle element, which is 650 (once 700 is included, we have 550, 600, 650, 700, and 750) to the parent node. When we split the leaf node, 550 and 600 go into the left leaf node and 700 and 750 go into the right leaf node.
When 650 gets promoted to the parent node, the parent node overflows because it can only hold 4 keys. Again 650 is the middle key (300, 500 650, 800, and 1000 are the keys) so we promote 650 to the root node and split the parent node. 300 and 500 move into one node and 800 and 1000 move into the other node. The resulting tree is shown below:
Dnode *InsertBefore(string value, Dnode *node);value is the string to be inserted into the doubly-linked list and it should be inserted before node. The return value should be the newly created node for value. Here is the declaration for Dnode:
class Dnode {
public:
string s;
Dnode *flink;
Dnode *blink;
};
Assume that the list has a sentinel node so you are always guaranteed
to have a predecessor node.
// prevNode is the node that precedes node. The new node must be inserted
// after prevNode and before node.
Dnode *InsertBefore(string value, Dnode *node) {
// create the new node and initialize its fields
Dnode *newNode = new Dnode;
Dnode *prevNode = node->blink;
newNode->s = value;
newNode->flink = node; // new node points forward to node
newNode->blink = prevNode; // new node points backwards to prevNode
prevNode->flink = newNode; // prevNode now points forward to new node
node->blink = newNode; // node now points backwards to new node
return newNode;
}