1.0 Introduction

Efficient state machine design using a Hardware Description Language (HDL), such as Verilog, can take many forms [1][2]. Are there specific forms that lend themselves well to synthesis? This paper describes some common coding styles and highlights two coding styles with registered outputs that are well suited for commonly used synthesis techniques.

This paper will briefly describe coding styles that generate combinational logic outputs and then will detail coding styles that generate registered outputs and describe why the registered output coding styles are often beneficial to synthesis strategies.

2.0 Basic FSM Structure

A typical block diagram for a Finite State Machine (FSM) is shown in Figure 1.

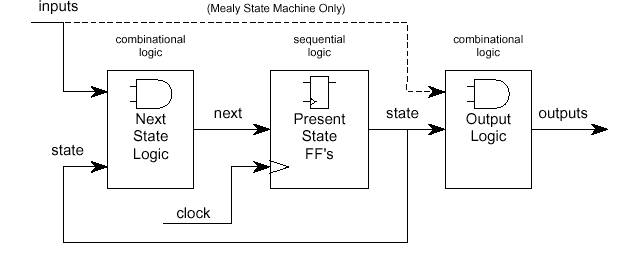
Figure 1 - FSM Block Diagram

A Moore state machine is an FSM where the outputs are only a function of the present state.

A Mealy state machine is an FSM where one or more of the outputs are a function of the present state and one or more of the inputs.

Both Moore and Mealy FSMs have been successfully implemented in digital designs. How the outputs are generated for these state machines is an interesting topic. Outputs are sometimes generated by combinational logic based on comparisons with a set of states, and sometimes outputs can be derived directly from individual state bits.

The code in Example 1 uses a common, efficient Verilog coding style to implement the state diagram shown in Figure 2.

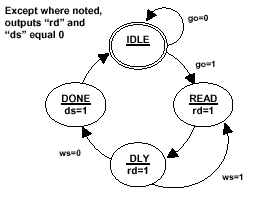
Figure 2 - FSM1 State Diagram

This coding style is sometimes referred to as a two-always block coding style with continuous assignment outputs. The first always block in this example is used to generate the sequential state register, the second always block is used to generate the combinational next state logic, and the continuous assignments are used to generate the combinational output logic.

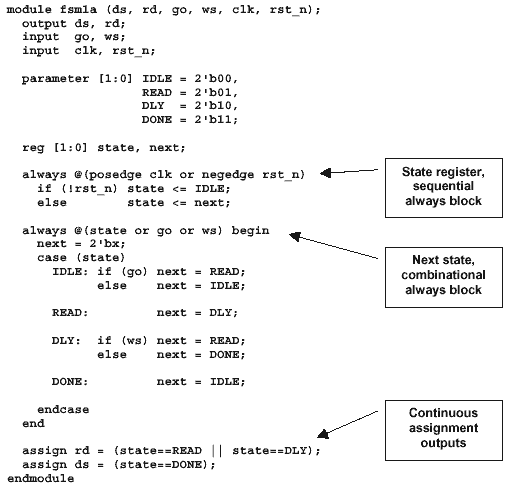
Example 1 - FSM Coding Style - Two-always blocks with continuous assignment outputs

The code in Example 2 is used to synthesize the same basic logic as Example 1, but the generation of the outputs is accomplished by moving the output equations into the same always block that is used to generate the combinational next state logic. This is a commonly used two-always block coding style.

Example 2 - FSM Coding Style - Two-always blocks with combined output assignments

The combinational outputs generated by these two coding styles (Example 1 and Example 2) suffer two principal disadvantages:

1. Combinational outputs can glitch between states.
2. Combinational outputs consume part of the overall clock cycle that would have been available to the block of logic that is driven by the FSM outputs.

When module outputs are generated using combinational logic, there is less time for the receiving module to pass signals through inputs and additional combinational logic before they must be clocked.

3.0 Partitioning For Synthesis

A popular and proven technique for partitioning a design for synthesis is to partition the design so that all outputs are registered and all combinational logic is on the input-side of a module as shown in Figure 3. This is sometimes referred to as "cloud-register" partitioning.

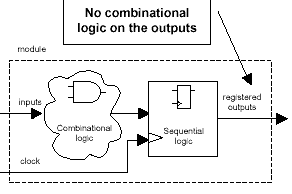
Figure 3 - "Cloud-register" module partition

A variation on the same synthesis technique is to partition the design so that all combinational logic is on the inputs or between registered stages within the module as shown in Figure 4.

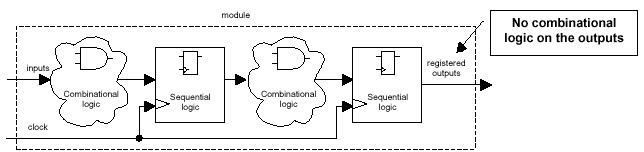
Figure 4 - Multi-stage module partition with registered outputs

The reason this technique is important is not that it necessarily makes a design any better, but that it greatly simplifies the task of constraining a design for synthesis.

Designs can be and have been successfully completed with combinational logic on both the inputs and the outputs of module partitions, but such designs complicate the task of constraining a design to meet timing requirements.

As shown in Figure 5, if a design requires a 10ns clock cycle, and if the output combinational logic of module A consumes 3.5ns, then the inputs of modules C and D and some of the inputs of module E must be constrained to use only 6.5ns (including setup time on registered elements). If module B consumes 5ns in the output combinational logic, then the other inputs of module E must be constrained to use only 5ns (including setup time on registered elements).

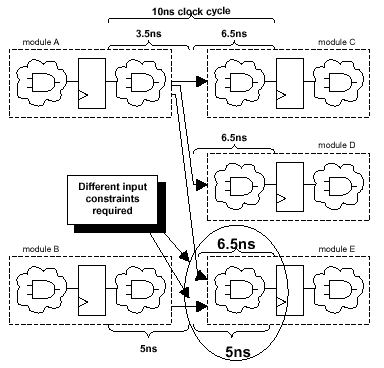
Figure 5 - Constraining combinational outputs that drive combinational inputs

For this simple 5-module design, the task of making these constraints is not too difficult, but imagine having to constrain dozens of inputs on the tens or hundreds of modules of a larger design, and making sure all of the constraints have been correctly set. This is one of the motivations behind registered module outputs.

4.0 Synthesis Time Budgeting

In a paper entitled "Evolvable Makefiles and Scripts for Synthesis", [3] Ekstrandh and Bell, describe a clever time-budgeting technique for synthesizing many modules by constraining inputs and outputs to sequential modules, and applying time-budget allotments to pure combinational modules. If pure combinational logic modules are removed and all sequential module outputs are registered, techniques similar to those described by Ekstrandh and Bell become even easier to implement.

One major argument against registered outputs is that redundant combinational logic might be required at the inputs of multiple receiving modules. In contrast, moving the combinational logic from some module outputs to the inputs of receiving modules might help suggest a different, more optimal partitioning of a design.

The best reason for moving combinational logic away from module outputs is that it significantly reduces synthesis scripting efforts that can lead to more easily meeting overall timing constraints. Tight constraints on output combinational logic in a driving module and tight timing constraints on input combinational logic in a receiving module generally does not yield the same efficient logic that could be inferred if all of the combinational logic could be optimized together with a larger overall timing constraint.

5.0 Registering FSM Outputs

Two good methods for coding FSMs so that all module outputs are registered include, (1) generating and registering "next-outputs", and (2) Encoding the state variables so that each output is one of the encoded bits of the registered state variable.

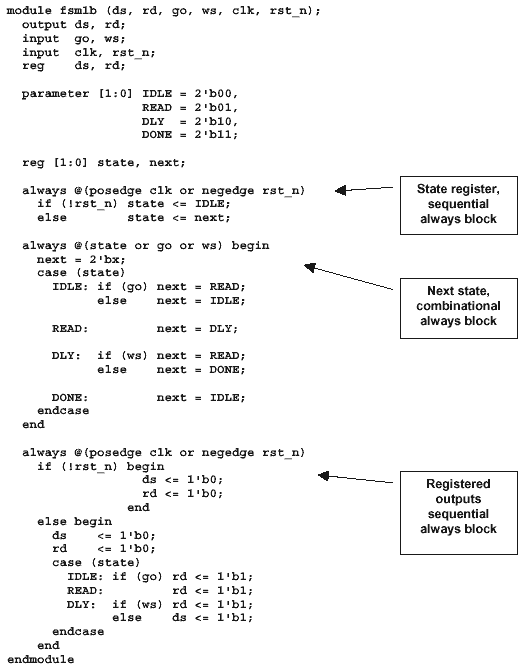
Example 3 - FSM Coding Style - Three-always block coding style

5.1 Three Always Block FSM

The first method commonly used to register the FSM outputs is to code a two always block FSM, the same as in Example 1, but instead of generating the outputs using continuous assignments, code a third block as a sequential always block to register the "next outputs" as shown in Example 3.

This method requires careful coding since this style forces an engineer to examine the present state and the inputs to determine what the "next outputs" will be. This method is somewhat error prone, but works fine if the outputs are properly coded.

The block diagram in Figure 6 shows the two sequential and one combinational logic blocks that are generated by the three always blocks.

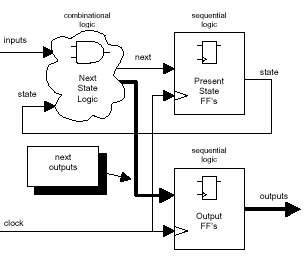
Figure 6 - FSM with registered outputs

5.2 One-Hot Output Encoding

A second interesting method for registering the FSM outputs is to select a state encoding that forces the outputs to be driven by individual state-register bits as shown in the block diagram of Figure 7.

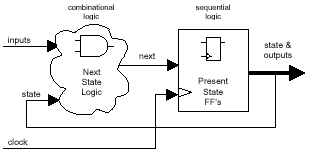
Figure 7 - FSM with registered outputs encoded as state bits

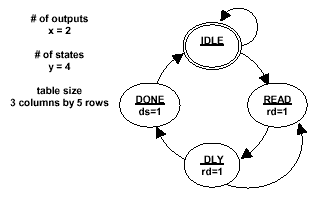
Figure 8 - Extracting table information from a state diagram

A structured method for encoding the outputs as part the state encoding is outlined in the following steps:

1. Count the number of outputs (x) and the number of states (y) in the state machine and start by making a table with y+1 rows and x+1 columns.

2. Starting at the second row in the left-hand column, make a list of all the FSM states, moving down the column for each state in the state machine. This will fill the left-hand column except for the top left-hand column cell.

3. Starting at the first row, second column and working to the right, list each FSM output as a separate column header.

Table 1 - Starting state table (redundant output patterns are circled)

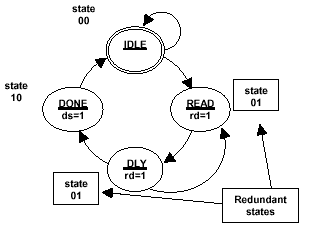
Figure 9 - One-hot output encoded redundant states

4. Place a "1" in each output column where an output is high for the listed states and place a "0" in each output column where an output is low for the listed states.

5. After filling out the entire table, search for output patterns that are the same for more than one state. If there are no duplicate patterns, use the output patterns in the table as state encodings. If all of the encodings are unique, no additional state bits are necessary and each state bit not only represents part of the state encoding, it also represents what will become a registered output bit.

Note: FSM inputs do not affect the state encodings. Only the number of states and the number of outputs affect the state encodings.

In general, the output patterns will not be unique to any one state and the following additional steps will be required:

6. Circle the duplicate output patterns in the table as shown in Table 1.

7. If there are two output patterns that are the same, one additional state bit will be required to create unique state encodings. If there are three or four output patterns that are the same, two additional state bits will be required to create unique state encodings. If there are between five and eight output patterns that are the same, three additional state bits will be required to create unique state encodings, etc.

Table 2 - State table after adding extra state bit column

8. Add a blank column between the state names column and the first output column and label this column "x0." Add another column for each additional required state bit, labeling each column "x1", "x2", etc.

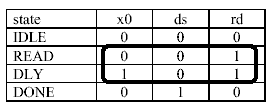
Table 3 - State table with unique state encodings

Fill the added columns with all zeros except for the circled redundant-encodings rows. Add binary encodings into the extra columns of the redundant-encoding rows to create unique state encodings as shown in Figure 10.

Figure 10 - One-hot output encodings with extra bits to create unique state encodings

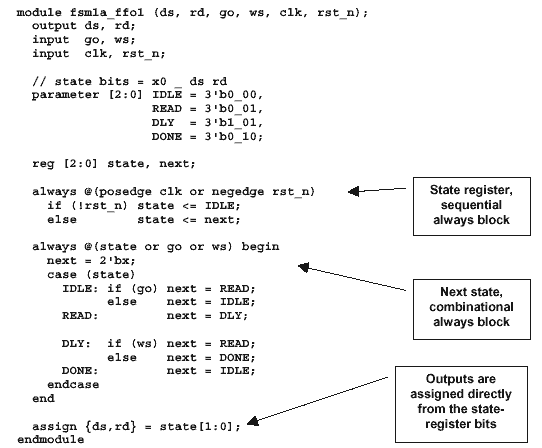
Example 4 - FSM Coding Style - One-hot outputs encoding

The state encodings in Table 3 will now be used to make Verilog parameter assignments to define each state encoding.

Now that the outputs have been incorporated into the state encodings, one or more continuous assignment statements can directly drive the outputs, where the actual state bits are used to drive the outputs. Since no additional glue logic is required to drive the outputs, the outputs will now be glitch-free.

The outputs of the Verilog state machine are now easily coded by making bit-select assignments from the state vector to each output, or by concatenating all of the outputs together into one continuous assignment and assigning all of the significant state bits to the outputs as shown in Example 4. If extra state bits were required to create unique state encodings, the output bits will be the LSBs of the state vector.

6.0 Mealy Outputs

Asynchronous Mealy outputs violate the synthesis guideline to partition a design into "cloud-register" groupings. An asynchronous Mealy output is an output that is a function of the present state and one or more inputs, which requires combinational logic to be placed on the Mealy outputs, forming a cloud of combinational logic after the register, as shown on the FSM module in the block diagram of Figure 11.

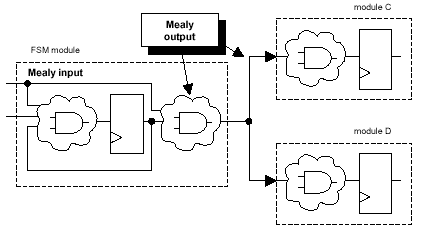
Figure 11 - FSM Mealy output driving combinational inputs

It is frequently feasible to move asynchronous Mealy outputs from an FSM module to the input or inputs of one or more modules (such as modules C and D as shown in Figure 12) that would have been driven by the Mealy outputs.

Figure 12 - Mealy logic partitioned separate from the FSM output

Transferring the Mealy logic from the output of the FSM module to the inputs of the driven modules might cause extra logic to be inferred because the logic has to be taken from a single output-"cloud" and added to potentially multiple input-"clouds." The undesirable, small increase in area due to the addition of redundant logic is generally offset by significantly simplifying the design effort and synthesis scripts.

7.0 Conclusions

• Partitioning designs so that there is no combinational logic on the outputs of an FSM significantly simplifies the task of synthesizing a multi-module design.
• Coding FSMs with registered outputs eliminates combinational output logic.
• Coding FSMs with registered outputs insures that the outputs will be glitch-free.
• The one-hot output encoding style is an efficient technique for coding FSMs to drive registered outputs directly from the state register bits.

References

[1] S. Golson, "State Machine Design Techniques for Verilog and VHDL," Synopsys Journal of High-Level Design, September 1994, pp. 1-48.

[2] C.E. Cummings, "State Machine Coding Styles for Synthesis," SNUG (Synopsys Users Group) 1998 Proceedings, section-TB1 (3rd paper), March 1998.