Sigma-Delta Modulator

Final Report

By,

Stephen C. Terry

&

Nazmul Islam

For the Course ECE 652

Course Instructor: Dr. Don Bouldin

Date: 6^th May 2003

Introduction:

Sigma-delta modulation techniques have been very successfully used in analog-to-digital conversion (ADC) applications over the last two decades. Although sigma-delta concepts existed since the middle of the century, only recent advances in VLSI technologies have made possible the appropriate handling of the bit stream generated by the 1-bit ADC.

Although now almost universally known a sigma-delta converter, these devices are still referred to by some manufacturers as delta-sigma converters. This term may be more appropriate in that, in its basic form, the converter consisted of a delta modulator (used for many years in telecommunications), where the input signal is added to the input of the integrator instead of its output (thus eliminating the need for an integrator at the receiver end) [1]. Unfortunately, with time the words delta and sigma seem to have been interchanged arbitrarily. Nowadays, a distinction seems to be made only when the relative position of the summing (sigma) block within the modulator is being emphasized. In addition to the above, other terms often found in the literature are over-sampling and noise shaping ADCs.

The last two terms are in fact evocative of the two basic principles involved in the operation of sigma-delta ADCs – over-sampling and noise shaping. The former spreads the quantization noise power over a bandwidth equal to the sampling frequency, which is much greater than the signal bandwidth. In the latter, the modulator behaves as a low-pass filter on the signal, and as a high-pass filter on the noise, thus "shaping" the quantization noise so that most of the energy will be above the signal bandwidth. A digital low-pass filtering stage then greatly attenuates out-of-band quantization noise, and finally, down-sampling brings the sampled signal to the Nyquist rate.

Sigma-delta ADCs are very extensively documented in the literature. The emphasis, however, seems to be either on very theoretical aspects involved in the technology, or on the traditional low-speed, high-resolution applications of these converters.

A very complete review of oversampling methods used for A/D and D/A conversion, as of 1992, is presented in [1]. The paper [2] also provides an up-to-date view of the technology, including an examination of its use in the A/D conversion of narrowband bandpass signals, as well as a discussion of several parallel architectures.

Advantages and disadvantages of sigma-delta ADCs

The penalty paid for the high resolution achievable with sigma-delta technology has always been speed - the hardware has to operate at the oversampled rate, much larger than the maximum signal bandwidth, thus demanding great complexity of the digital circuitry. Because of this limitation, these converters have traditionally been relegated to high-resolution, very-low frequency applications (Figure 1), and more recently speech, audio and medium speeds (100 kHz to 1 MHz).

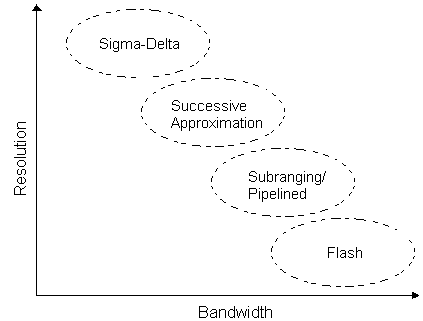
Figure 1: A/D Converter technologies, resolution and bandwidth

The digital filtering stage results in long latency between the start of the sampling cycle, and the first valid digital output; similarly, there is a significant lag thereafter between digital outputs and their corresponding sampling instants. This characteristic has prevented the use of these converters in multiplexed systems - it takes many clock cycles for the digital filter to settle after switching from one channel to the next.

By having thus outlined the key limitations of these devices, we've established the framework within which they are suitable, and may now proceed to itemize their numerous advantages when compared with alternate technologies:

• Most of the circuitry in sigma-delta converters is digital. This implies that performance will not drift significantly with time and temperature. Also, incorporation of the converter into a single-chip package with additional circuitry, such as a D/A converter (Codec), microcontroller, or DSP is feasible. Finally, the cost of implementation is low and will continue to decrease.

• They are inherently monotonic (i.e., a change in the digital output has always the same slope as the analog input). This is of particular importance in closed-loop control systems, where misinterpretation of the direction of change of a measured variable may cause the system to become unstable.

• They are inherently linear, and present little differential non-linearity.

• They do not require an external sample & hold circuit; due to the high input sampling rate and low precision of the A/D conversion, the devices are inherently self-sampling and tracking.

• Requirements for analog anti-aliasing filters are minimum - in most cases, a simple single pole RC-filter suffices. In contrast, the filters required for medium- to high-resolution applications using other (non-oversampling) technologies are very sophisticated, difficult to design, large, and expensive.

• The background noise level, which determines the SNR, is independent of the input signal level.

• Since there is a digital filtering stage after the A/D converter section, noise injected during the conversion process can be controlled very effectively. In fact, the filter may be tailored to minimize noise with very specific characteristics (e.g., 60 Hz).

• As stated above, their mostly digital nature makes these devices relatively inexpensive. In multichannel applications, a one-converter-per-channel architecture will often be more cost-effective than a single (very fast, non-oversampling) converter with multiplexed inputs.

Modulator architectures and implementation problems

The structure of the basic first-order sigma-delta converter is shown in Figure 2. The modulator consists of an integrator and a comparator, with a 1-bit DAC in a feedback loop. The digital decimator that follows performs both, digital filtering and down-sampling of the 1-bit input data stream.

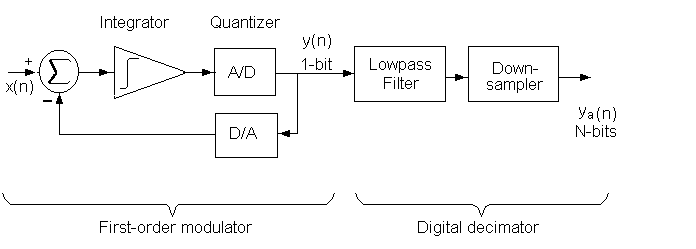
Figure 2: First sigma-delta A/D converter

Descriptions of the operation of this converter, both in time and frequency domains, abound in the literature (see for example [1], [2], [3]). The nonlinear nature of the devices makes precise analysis difficult, especially when higher order architectures are used; in fact, in many cases behavior has only been possible to characterize through simulations. Here we limit ourselves to a brief discussion of common variations of the basic architecture, and implementation problems that might be expected.

Even the very simple first-order modulator can achieve very attractive SNRs; a good "rule of thumb" is that for every doubling of the oversampling ratio, the SNR will improve by approximately 9 dB [2]. In this architecture, imperfections in the integrator usually don't present significant difficulties, unless the oversampling ratio is extremely large. Similarly, constraints on the accuracy of integrator and DAC gains are quite lax - typically, the gain is implemented as a ratio of two capacitors, and the precision required in their matching is of only 1 part in 10. With regard to the quantizer, we observe that any noise introduced by nonlinearities is subject to noise shaping by the modulator, and has therefore little effect on SNR.

A significant problem with the basic first-order system, resulting directly from its nonlinear nature and feedback, is the presence of limit cycle oscillations. This will produce periodic or "tone" components in the output in response to DC inputs, or even small amplitude sinusoidal inputs. Clearly, these tones are highly undesirable in audio/speech applications; for this reason, even when the overall SNR may be very good, first-order modulators are practically never used in these areas.

Conceptually, the extension to a second-order modulator is quite straightforward. By incorporating a second integrator more quantization noise is "pushed" outside the passband. In this case, every doubling of the oversampling ratio results in a 15 dB increase in SNR.

With two integrators, we are now concerned with the accuracy of both their gains. Fortunately, it has been shown [2] that these are (relatively) insensitive to deviations from their nominal values over quite a wide range of oversampling ratios. The problem with limit cycles remains however, resulting in idle tones for DC or low amplitude sinusoidal inputs; also, unlike in the first-order case, the limit cycles are now dependent on the initial condition of the output. Furthermore, an additional potential problem with a second-order modulator that uses a single-bit quantizer, is that of "overloading"; this may produce harmonic distortion tones for sinusoidal inputs, as well as significant tone components near f_s/2.

In addition to further improving SNR, higher than second-order modulators will also alleviate some of the problems with idle tones. In general, for an N-order modulator every doubling of the oversampling ratio provides an additional (6N + 3) dB of SNR. A great variety of topologies have been implemented [1,2], and very often these are patented by the manufacturers. Clearly, the complexity of the circuitry increases dramatically, (conditional) stability is harder to achieve, and exact analysis is seldom possible.

Higher-order modulation can also be achieved by cascading several lower-order stages. This avoids problems with stability, while maintaining the advantages with respect to SNR and limit cycles. Fourth-order modulators consisting of the cascading of two second-order stages are common.

There are also architectures that employ multi-bit quantizers. For example, in a second-order modulator, each additional bit in the quantizer results in a SNR improvement of about 6 dB. The stability of these systems is easier to predict (since a linearized model will more accurately represent the system), and idle tone problems are also alleviated. On the other hand, because of the linearity required for high-resolution converters, the multi-bit DAC is more difficult to fabricate.

Overview of Sigma-Delta Converter Development in 1.8V/0.18mm CMOS

Implementing an analog or mixed-signal system in a 1.8V digital CMOS technology poses many challenges. First, the low power supply voltage means that dynamic range is at a premium. In this work several steps were taken to ensure robust operation at low voltages, including the use of dynamically biased low voltage cascode current mirrors (LVCCM) in the integrator. The second major design challenge is that this technology does not include linear capacitors as an option. Linear capacitors are extremely important in many data converters because they form the backbone of switched-capacitor circuits. The most common application of switched-capacitor circuits in sigma-delta data converters is in the integrator. Considering that linear capacitors were not available, it was decided that a continuous-time, current-mode integrator would be used instead of the more traditional switched-capacitor integrator. The main advantage of the current-mode integrator is that it possible to bias the integrator such that the gate capacitance of a MOSFET can be used as a linear capacitor. Thus, a high performance sigma-delta converter can be realized in a digital CMOS technology that does not have linear capacitors.

In order to further investigate sigma-delta data converter develop in a deep sub-micron, digital CMOS process, the critical components used in a sigma-delta have been laid out and simulated and are now ready for fabrication. These cells include a non-overlapping clock generator, high-performance clocked comparator, and a current-mode integrator. The next step in the development process is to fabricate and test these individual cells to insure that their performance is adequate for the sigma-delta requirements. Additionally, during testing it will be possible to build a sigma-delta converter out of the fabricated components, and thus the performance of the complete converter can be evaluated.

Comparator Design:

Comparators are a key component in a data-converters because they represent the link between the analog and digital domains (i.e. analog signal in and digital level out). To get an efficient Sigma-Delta Converter we need a high-speed comparator with high resolution. This comparator can achieve 8-b accuracy with sampling rate up to 65 MHz.

It consists of a differential input pair, a CMOS latch circuit (both n-channel and p-channel flip-flop) and an S-R latch (generates CMOS compatible output voltage). We have used two non-overlapping clock named S1 & S2 in the circuit. To generate the non-overlapping clock the clock generation circuit was also generated.

After doing the pre-layout simulation, the post-layout simulation was done. Pre-layout give a delay of 97.6 pico-sec, on the other hand the Post-layout gave a delay of 104 pico-sec. The reason behind the high delay in post-layout simulation is there creates extracted capacitance in the post layout simulation.

Figure 3: Schematic of Comparator

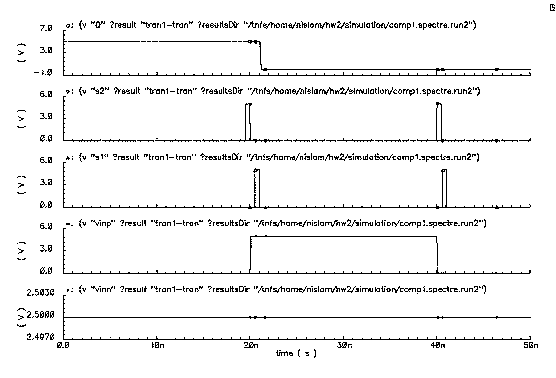
Figure 4: Pre-Layout Simulation of Comparator

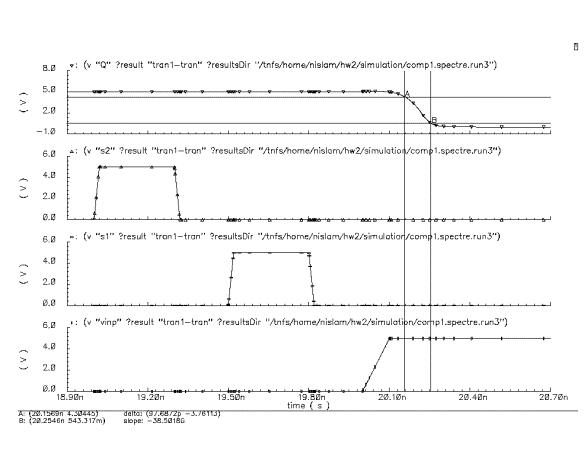
Figure 5: Zoomed Pre-Layout Simulation of Comparator

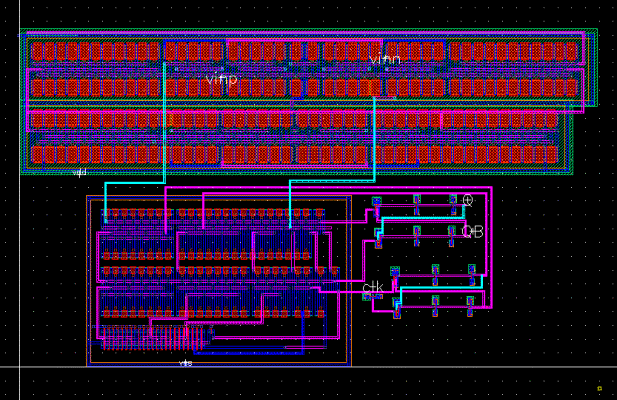
Figure 6: Layout of the Comparator

Figure 7: Zoomed version of Post-Layout Simulation of Comparator

Integrator Design:

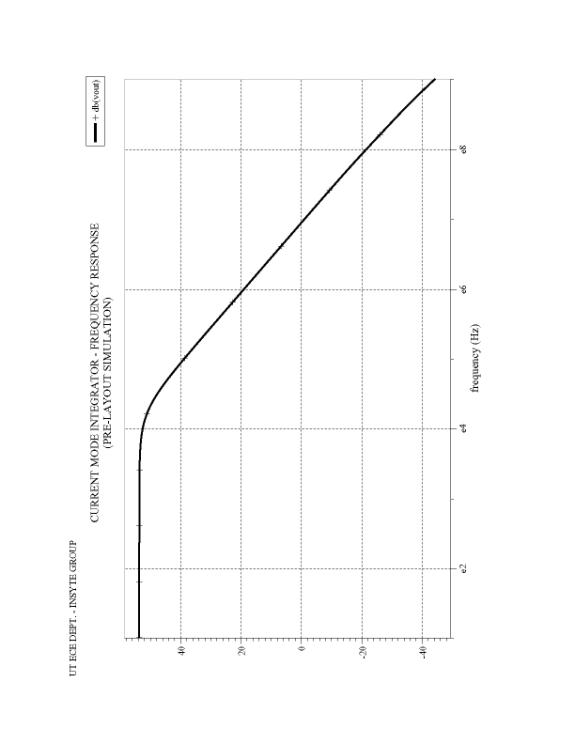
The integrator is perhaps the most important component in a sigma-delta converter because it determines the noise floor and dynamic range. As stated previously, it was decided in this project to use a current-mode integrator because linear capacitors are not available in this technology. If linear capacitors were available, a switched capacitor integrator would be used. Figure 8 presents the integrator schematic, which is based on the integrator presented in [4]. Notable in this implementation is the cascode operation at 1.8V power supply, which is facilitated by the dynamically biased NMOS cascode current mirrors. Additionally, the bias current for each leg of the integrator is 100mA. Figure 9 presents the Smartspice simulation for the integrator. One can see that the integrator has a finite DC gain of roughly 50dB with a dominant pole at 10 kHz. The integrator layout is shown in Figure 10. Notable in the layout is the extensive use of common-centroid symmetry. Finally, Figure 11 presents the Smartspice simulation for the post-layout extraction of the integrator. As one can see, there is very little difference between Figures 9 and 11.

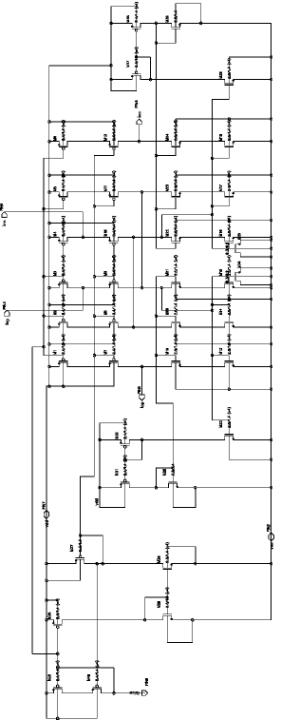
Figure 8: Cadence Schematic of Current-Mode Integrator

Figure 9: Pre-Layout Simulation of Current-Mode Integrator

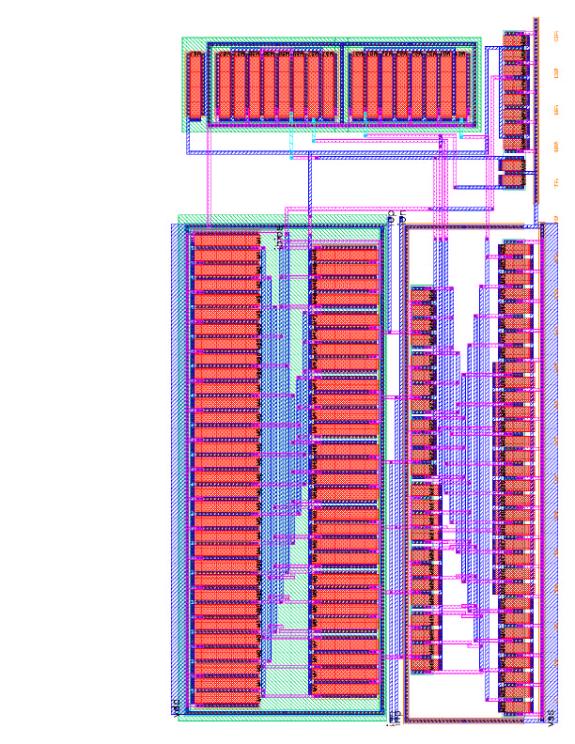
Figure 10: Integrator Layout in 0.18mm CMOS technology

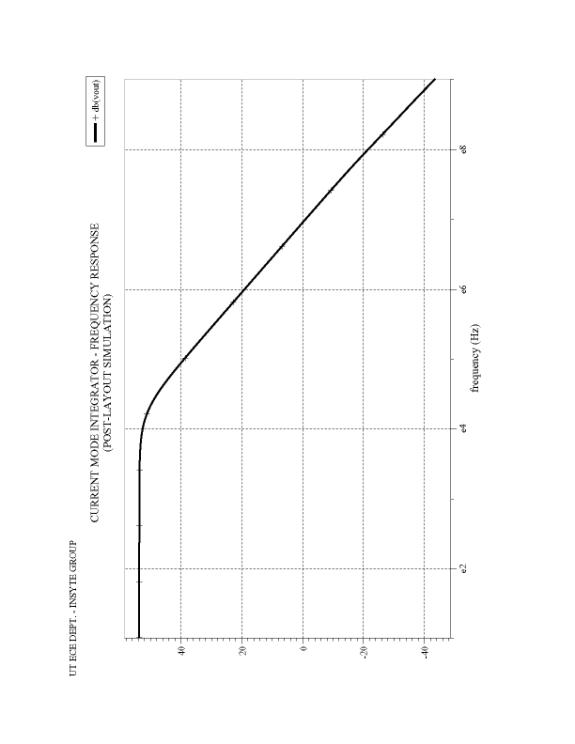
Figure 11. Post-Layout Integrator Simulation

Conclusion

We have presented the design, layout, and simulation of components required in a sigma-delta data converter. These cells are now ready for fabrication and testing. The most notable aspect of this design is that all cells have been operate at 1.8V, and no cell requires linear capacitors. The next step in this work will be to measure the actual performance of the different system components and make any adjustments that necessary so that this work can be targeted to a SOC.

References

[1] J. Candy and G. Temes, "Oversampling methods for A/D and D/A conversion," in Oversampling Delta-Sigma Data Converters, pp.1-25, IEEE Press, 1992.

[2] P.M. Aziz, H.V. Sorensen and J. Van Der Spiegel, "An overview of sigma-delta converters," IEEE Signal Processing Magazine, Vol.13, No.1, Jan. 1996.

[3] Analog Devices, "Sigma-delta conversion technology," DSPatch - Digital Signal Processing Applications Newsletter, Winter, 1990.

[4] R.H. Zele and D.J. Allstot, “Low Power CMOS Continuous-Time Filters,” IEEE J. Solid-State Circuits, vol. 31, no.2, Feb. 1996, pp. 157 – 168.