CS140 -- Final Exam: Answers and Grading Guide

December 15, 1998

Question 1

The code is in q1.c. Run it if you have any questions.

Start with -20. Then add 5 for the first ``total++.'' Then add 5*2 for the second one. The total is -5. Run the code yourself (add some print statements) if you're confused.

You got 2 points for answering -5. One point for -8.

Question 2

Similarly, you start with -20, then you'll iterate n+1 times in the outer loop. This will increment total n+1 times. Assume n is a power of two. The inner loop runs log(n) times. Thus, you'll get (n+1)log(n) iterations of the inner loop. The final value of total is therefore:

-20 + (n+1) + (n+1)log(n) = n*log(n) + n + log(n) - 19

You got 4 points for answering n*log(n) + n + log(n) - 19 or its equivalent. You got 3 points for n*log(n) + n - 20, 2 points if you gave something that was Theta(n*log(n)), and one point if youf answer had a log(n) in it.

Question 3

The biggest term is the n*log(n) term. Therefore:

. g(n) = 1 g(n) = log(n) g(n) = n g(n) = n*log(n) g(n) = n*n

f(n) = O(g(n)) . . . X X

f(n) = Omega(g(n)) X X X X .

f(n) = Theta(g(n)) . . . X .

f(n) = o(g(n)) . . . . X

Grading here went as follows. You got four points total for big-O terms, two points for the Omega terms, two points for the Theta term, one point for little-o. You were penalized for marking incorrect boxes.

You were graded relative to the answer you put down in Question 2. Thus, if you put down something where the dominant term is n*n, then your answer should have been:

. g(n) = 1 g(n) = log(n) g(n) = n g(n) = n*log(n) g(n) = n*n

f(n) = O(g(n)) . . . . X

f(n) = Omega(g(n)) X X X X X

f(n) = Theta(g(n)) . . . . X

f(n) = o(g(n)) . . . . .

If your answer to question two had a dominant term that is linear, then your answer should have been:

. g(n) = 1 g(n) = log(n) g(n) = n g(n) = n*log(n) g(n) = n*n

f(n) = O(g(n)) . . X X X

f(n) = Omega(g(n)) X X X . .

f(n) = Theta(g(n)) . . X . .

f(n) = o(g(n)) . . . X X

If your answer to question two had a dominant term that is log(n), then your answer should have been:

. g(n) = 1 g(n) = log(n) g(n) = n g(n) = n*log(n) g(n) = n*n

f(n) = O(g(n)) . X X X X

f(n) = Omega(g(n)) X X . . .

f(n) = Theta(g(n)) . X . . .

f(n) = o(g(n)) . . X X X

And finally, if your answer to question two had a dominant term that is constant, then your answer should have been:

. g(n) = 1 g(n) = log(n) g(n) = n g(n) = n*log(n) g(n) = n*n

f(n) = O(g(n)) X X X X X

f(n) = Omega(g(n)) X . . . .

f(n) = Theta(g(n)) X . . . .

f(n) = o(g(n)) . X X X X

Question 4

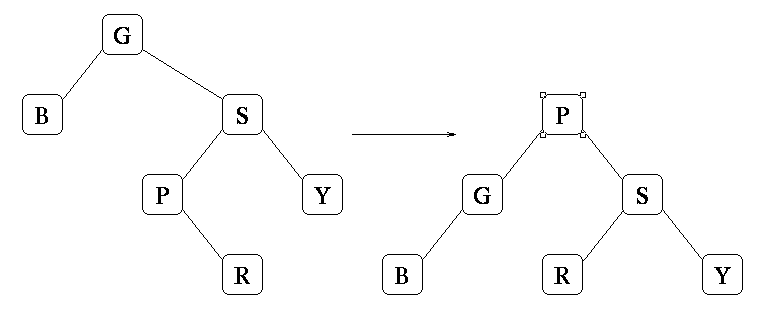
Grading: 2 points for getting it right.

Question 5

First you insert the R, and the tree looks as in Question 4. This is imbalanced around node G, and needs to be fixed with a double rotation about node P:

Grading: 4 points for getting it right. 2 points if you had a valid AVL tree (with all the right elements). Zero otherwise.

Question 6

First you insert the T, and the tree looks as in the left diagram below. This is imbalanced around node G, and needs to be fixed with a single rotation about node S:

Grading: 4 points for getting it right. 2 points if you had a valid AVL tree (with all the right elements). Zero otherwise.

Question 7

First you insert the R, and the tree looks as in the left diagram below. Now you have to splay R to the top. First you do a double rotation about R as depicted, and then R is one node from the root. You get it to the root with a single rotation about node R.

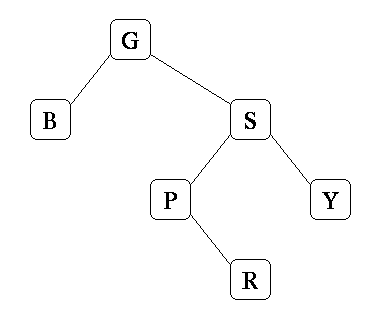
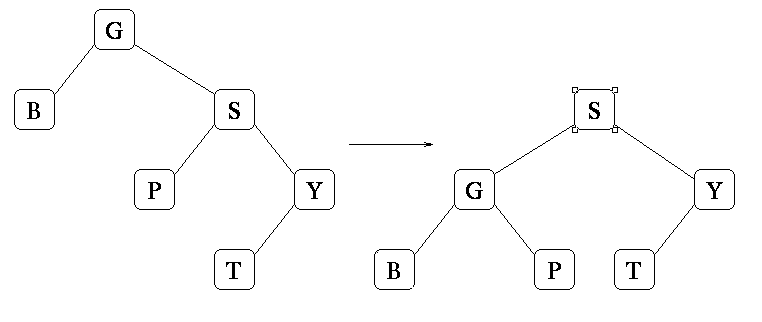
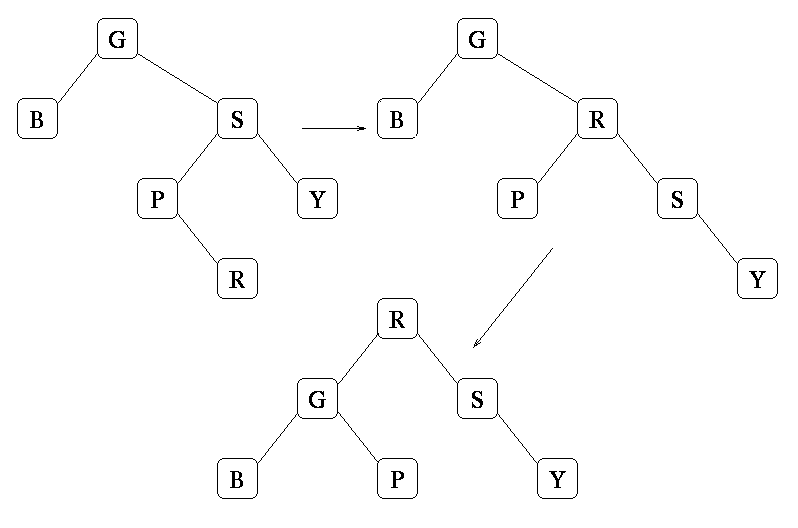
Grading: 4 points for getting it right. 2 points for a valid tree with R at the root.

Question 8

First you insert the A, and the tree looks as in the left diagram below. Now you have to splay A to the top. This is done with a zig-zig transformation -- rotate about B and then about A:

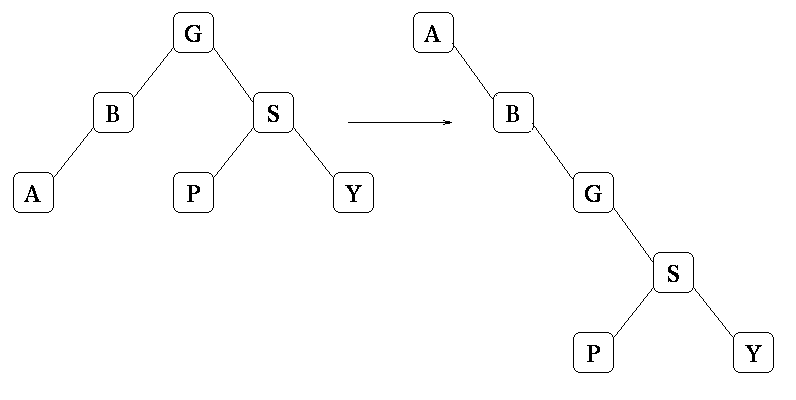
Grading: 4 points for getting it right. 2 points for a valid tree with A at the root.

Questions 9-20

Two points each.

Question 9: a (constant time).
Question 10: c -- you may get up to n collisions. One point for answering a.
Question 11: c -- the tree does not have to be balanced. One point for answering b.
Question 12: b -- one of the nice properties of a balanced binary tree.
Question 13: c -- the tree is not always balanced. See the book for examples. One point for answering b.
Question 14: d -- this is the nice property of splay trees.
Question 15: a -- a constant number of pointer swaps.
Question 16: b.
Question 17: d. n operations at O(log(n)) each.
Question 18: e -- if you insert n elements that are already sorted, your tree will have depth n. One point for answering d.
Question 19: c -- use recursion -- you make one call per node. One point for answering d, since this you had to deal with the red herring of the flink and blink pointers.
Question 20: c -- obviously linear with the flink and blink pointers.

Question 21

The answer is e. First collision is at 71, which goes into entry 2. Then at 52, 10 and 4 which go into entries 4, 5 and 6 respectively.

No partial credit.

Question 22

The answer is f. First collision is at 71, which goes into entry 2. Next is 52, which looks at entry 3 and finds it occupied, so it looks at entry 2+4=6, and goes there. 10 then collides at entries 0 and 1 and then looks at entry 0+4=4, and puts it there. Finally, 4 collides with 10 and goes into entry 5.

No partial credit.

Question 23

The correct answers are b, d, e and g. The only really tricky one is g. Think about it.

Grading was as follows: 2 points for each right answer. -2 for each wrong answer. Minimum score was zero.

Question 24

The ordering of calls is:

visit(X)
  visit(R)
    visit(M)
      visit(G)
        print(G)
      visit(P)
        print(P)
      print(M) 
    visit(V)
      visit(U)
        visit(T)
          print(T)
        print(U)
      visit(W)
        print(W)
      print(V)
    print(R)
  print(X)

This makes:

G
P
M
T
U
W
V
R
X

You got 4 points for that. 2 points for a reverse postorder traversal (WTUVPGMRX). Otherwise, you got a point if the last thing printed was X.

Question 25

int nnodes(BstreeNode *b) {
  if (b == NULL) return 0;
  return 1 + nnodes(b->left) + nnodes(b->right);
}

8 points for something that works, like the above. 6 points if you forget to test for NULL. 2 points for something recursive. 0 otherwise.

Question 26

This is really easy -- just push onto the front of the list and pop off the front. Since dllists and stacks are both (void *)'s, you don't even need to cast, so I didn't take off if you omitted casting.

#include < stdio.h >
#include "dllist.h"

Stack new_stack()
{
  return (Stack) new_dllist();
}

free_stack(Stack s)
{
  free_dllist((Dllist) s);
}

int stack_empty(Stack s)
{
   return dll_empty((Dllist) s);
{

stack_push(Stack s, Jval val)
{
  dll_prepend((Dllist) s, val)
}

Jval stack_pop(Stack s)
{
  Jval retval;

  retval = stack_top(s);
  dll_delete_node(dll_first((Dllist) s));
  return retval;
}

Jval stack_top(Stack s)
{
  if (stack_empty(s)) {
    fprintf(stderr, "Error: trying to look at the top of an empty stack\n");
    exit(1);
  }
  return (dll_val(dll_first((Dllist) s)));
}

Point allocation was as follows:

Two points for new_stack().
Two points for free_stack().
Two points for stack_empty().
Three points for stack_push().
Four points for stack_pop(), allocated as follows:
- One for error checking (or letting stack_top() error check for you).
- One for saving the value in the first node.
- Two for getting the dll_delete_node() right.
Four points for stack_top(), allocated as follows:
- One for error checking (or letting stack_top() error check for you).
- One for finding the front of the list correctly.
- Two for returning the right thing (not the node, but the val field).

.	g(n) = 1	g(n) = log(n)	g(n) = n	g(n) = nlog(n)*	g(n) = nn*
f(n) = O(g(n))	.	.	.	X	X
f(n) = Omega(g(n))	X	X	X	X	.
f(n) = Theta(g(n))	.	.	.	X	.
f(n) = o(g(n))	.	.	.	.	X