CS140 Final Exam: December 7, 2004

Answer to Question 1

Part 1: Look at the implementation of dll_append. This is a malloc() and a few pointer operations. Answer: a.
Part 2: In the worst case, the splay tree is a line, as in Question 4, and the operation has to go over every element. Splay trees guarantee good behavior over collections of operations, not over single operations. Answer: c.
Part 3: AVL trees guarantee that insertion and find operations are in log time: Answer: b.
Part 4: In the worst case, all n elements are consecutively located, and you try to find an element that requires you to search all n elements. Answer: c.
Part 5: All tree traversals visit each node and link once. There are n nodes and n-1 links. Answer: c.
Part 6: This performs a constant number of pointer operations: Answer: a.
Part 7: Here is where the performance of splay trees is good -- the operations average to be logarithmic: Answer: d.
Part 8: Straightforward: Answer: d.
Part 9: This creates a line, and is the worst-case for binary trees: Answer: e.
Part 10: Again straightforward: Answer: d.

Answer to Question 2

Part 1

63 mod 32 equals 31. Since elements 31, and 0 through 3 are taken, the element will go into location 4.

Part 2

With quadratic probing, we test h, which equals 31. It is taken, so we test (h+1*1)%32, which equals 0. That is taken, so we test (h+2*2)%32, which equals 3. That is taken, so we test (h+3*3)%32, which equals 8. That is also taken, so we test (h+4*4)%32, which equals 15. That one is free, so that is where it goes. Answer = 15.

Answer to Question 3

There exist positive constants n and m such that for all values of r greater than n, m*b(r) > a(r). That is answer e. The only other answer that makes any sense is n, although it does not define what r_0 is. If r_0 is a positive constant, and n equals 1 (which of course is a positive constant), then you'll note that answer n is equivalent to answer e. None of the other answers are even close.

Answer to Question 4

Part 1

Part 2

Answer to Question 5

Part 1

The internal nodes hold the minimum keys of all but their leftmost subtrees. So:

Part 2

When 15 is added, the external node holding it has five values, so the node must be split into two nodes, one with three values, and one with two. This adds an extra link to its parent, which now has five links, so it too must be split. If we split the left sides of each node into two, and the right sides into three, then the resulting tree is:

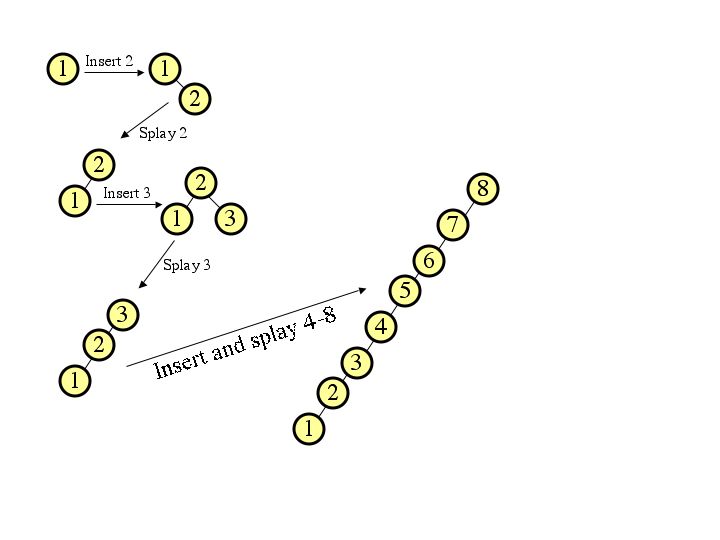
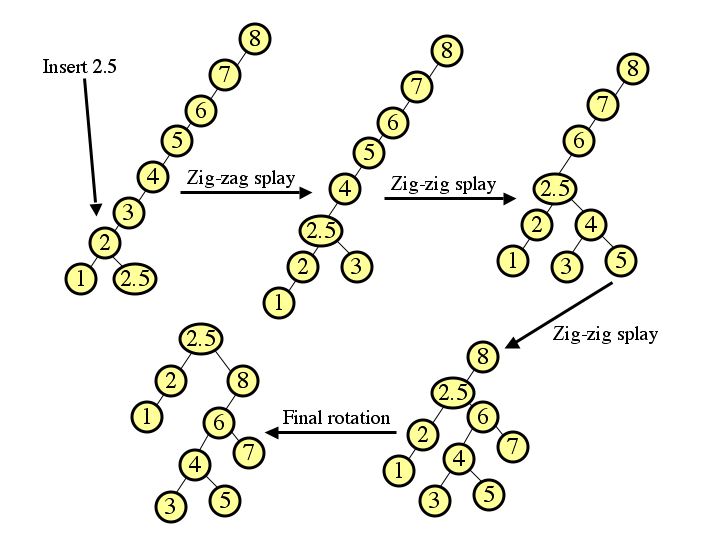
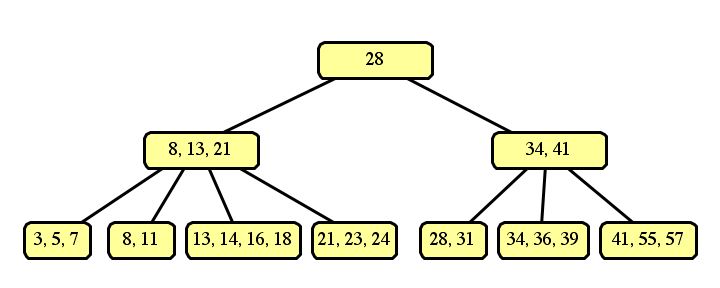
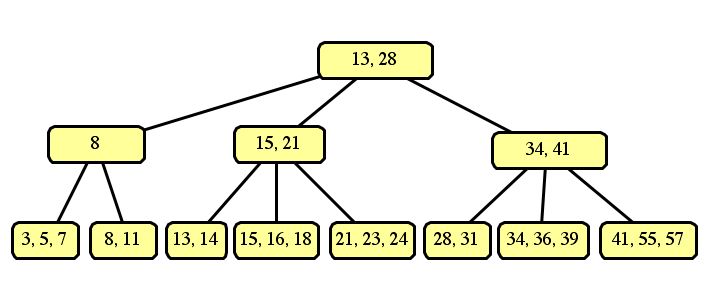
If we split the left sides of each node into three, and the right sides into two, then the resulting tree is:

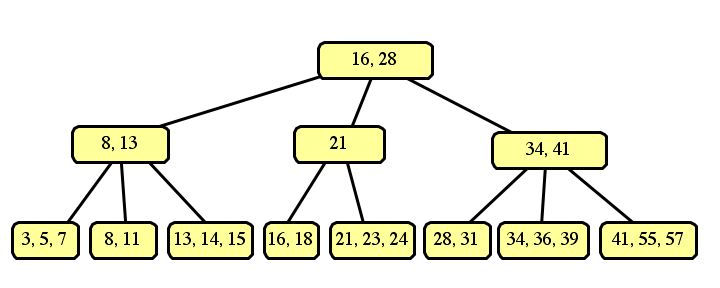
These are the only two correct answers. An optimization of B-trees would "borrow" a slot from a neighboring node, such as:

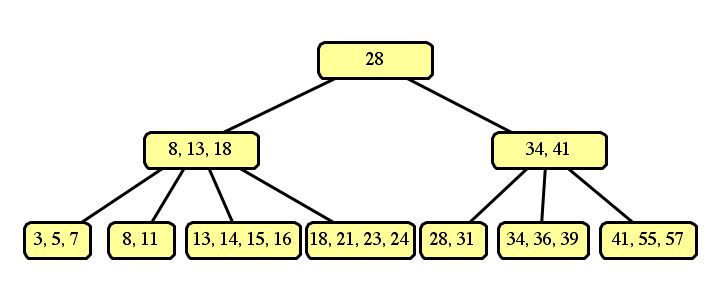
However, this answer did not receive full credit, since it is not part of the standard definition of B-Trees.

Answer to Question 6

This is a very simple recursival postorder traversal. If my left subtree is a binary search tree whose maximum key is less than mine, and my right subtree is a binary search tree whose minimum key is greater than mine, then this is a binary search tree:

int is_bstree(BTreeNode *root, double *min, double *max)
{
  double subtree_min, subtree_max;

  if (root->left == NULL) {
    *min = root->key.d;
  } else {
    if (!is_bstree(root->left, &subtree_min, &subtree_max)) return 0;
    if (subtree_max >= root->key.d) return 0;
    *min = subtree_min;
  }

  if (root->right == NULL) {
    *max = root->key.d;
  } else {
    if (!is_bstree(root->right, &subtree_min, &subtree_max)) return 0;
    if (subtree_min <= root->key.d) return 0;
    *max = subtree_max;
  }

  return 1;
}

Answer to Question 7

Here is what the tree looks like after reading in the input data:

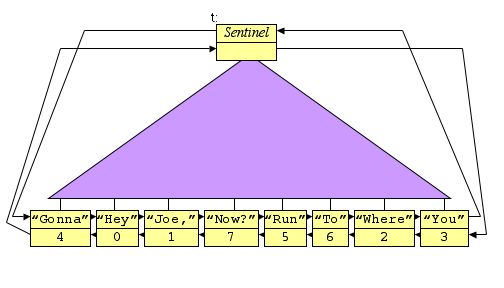
So, it will print out:

Character 4 of "Gonna": "a"
Character 0 of "Hey": "H"
Character 1 of "Joe,": "o"
Character 7%4=3 of "Now?": "?"
Character 5%3=2 of "Run": "n"
Character 6%2=0 of "To": "T"
Character 2 of "Where": "e"
Character 3%3=0 of "You": "Y"

Meaning the answer is: aHo?nTeY

You can cut/paste the program and try it yourself if you want.