CS202 Final Exam - December 6, 2021 - Answers and Grading

Question 1 - 6 points

This was a multiple choice, and on canvas, the answers were shuffled. Here's an example:

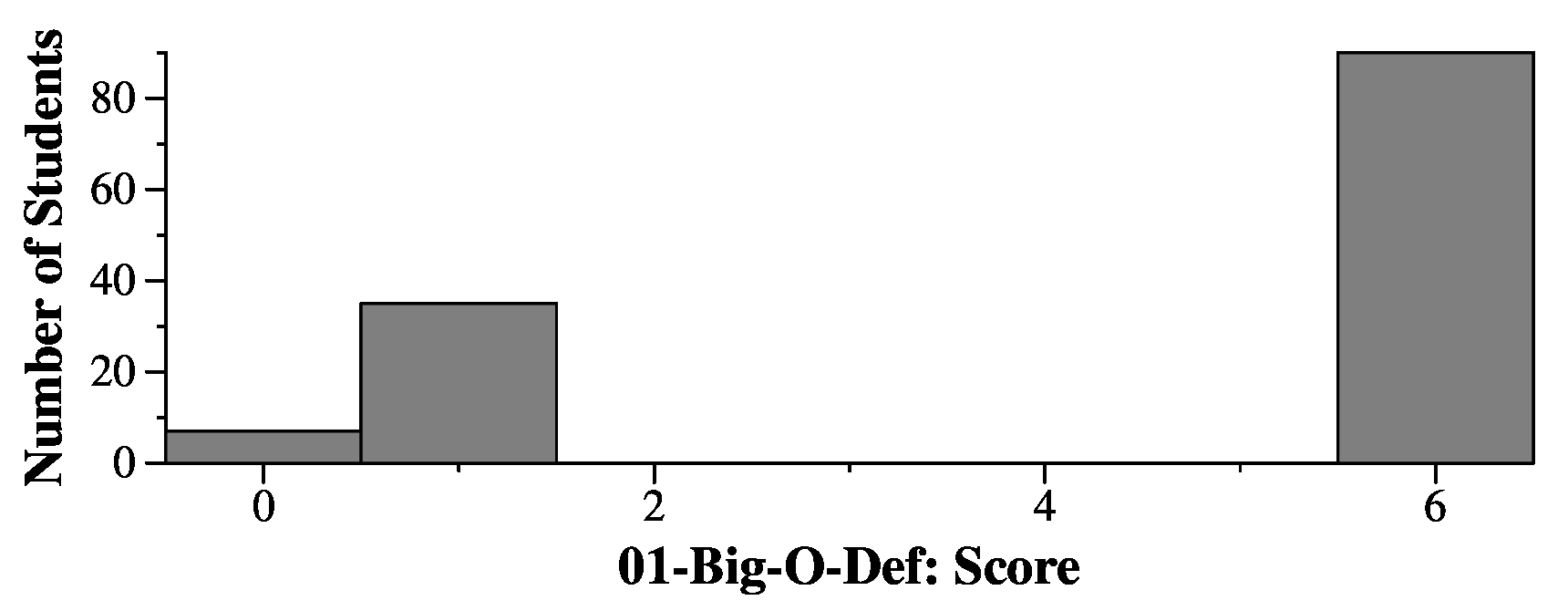
If f(n) = O(g(n)), then:

A. There exist positive constants x and y such that for all n > x, y * f(n) > g(n).
B. There exist positive constants x and y such that for all n < x, y * g(n) > f(n).
C. There exist positive constants x and y such that for all n < x, y * f(n) > g(n).
D. There exist positive constants x and y such that for all n > x, y * g(n) > f(n).

The answer is D. Straight from the definition of big O.

Question 2

These were from a bank of five similar, but different questions. Here's an example:

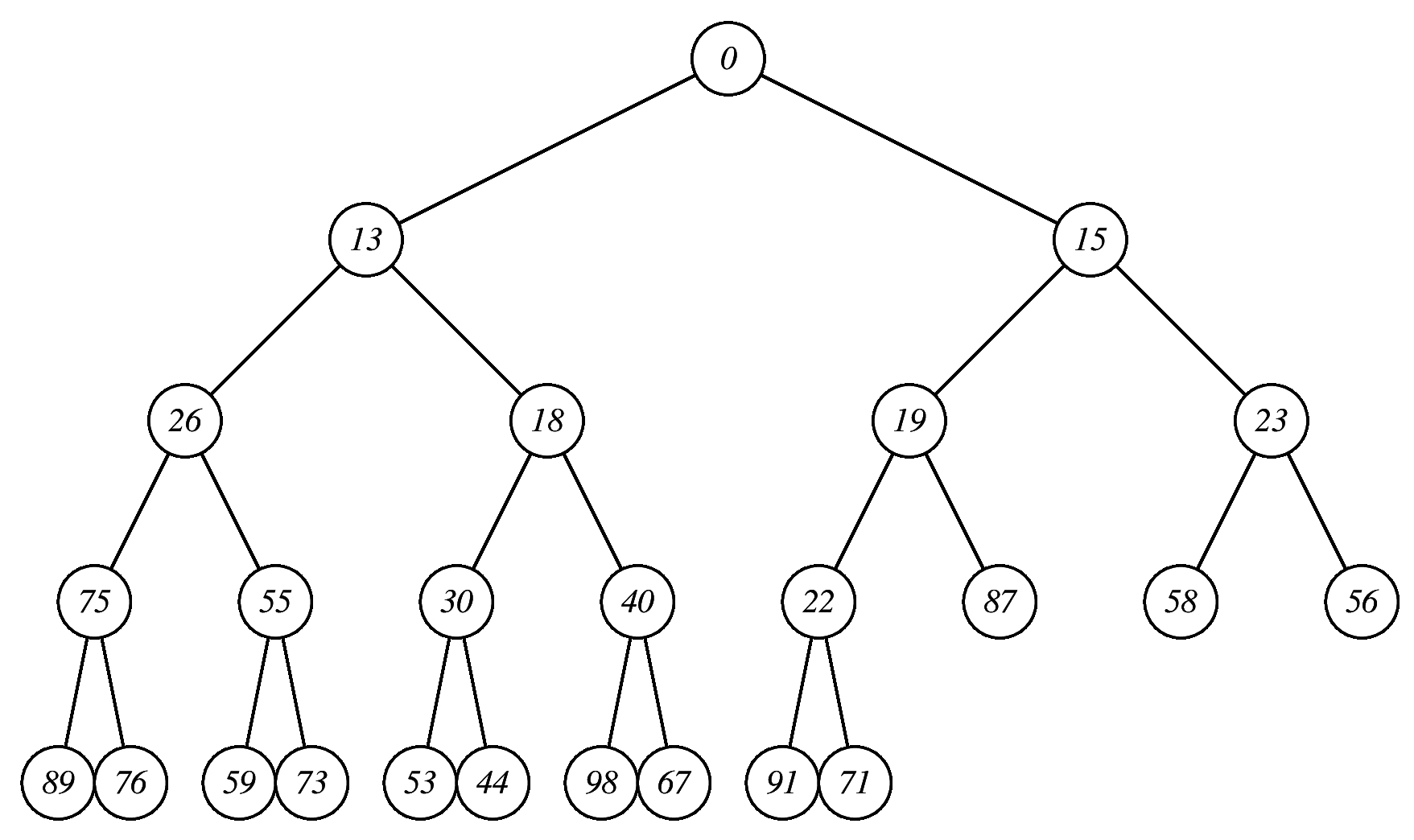Suppose that Logan pushes the value 4 into the heap pictured above. When the resulting heap is stored in a vector named h, please tell me the following:

What is the value at index 1 of h (in other words, h.at(1))
What is the value at index 2 of h (in other words, h.at(2))
What is the value at index 5 of h (in other words, h.at(5))
What is the value at index 6 of h (in other words, h.at(6))
What is the value at index 11 of h (in other words, h.at(11))
What is the value at index 12 of h (in other words, h.at(12))
What is the value at index 24 of h (in other words, h.at(24))
What is the value at index 25 of h (in other words, h.at(25))

The result of push(4) is the following heap:

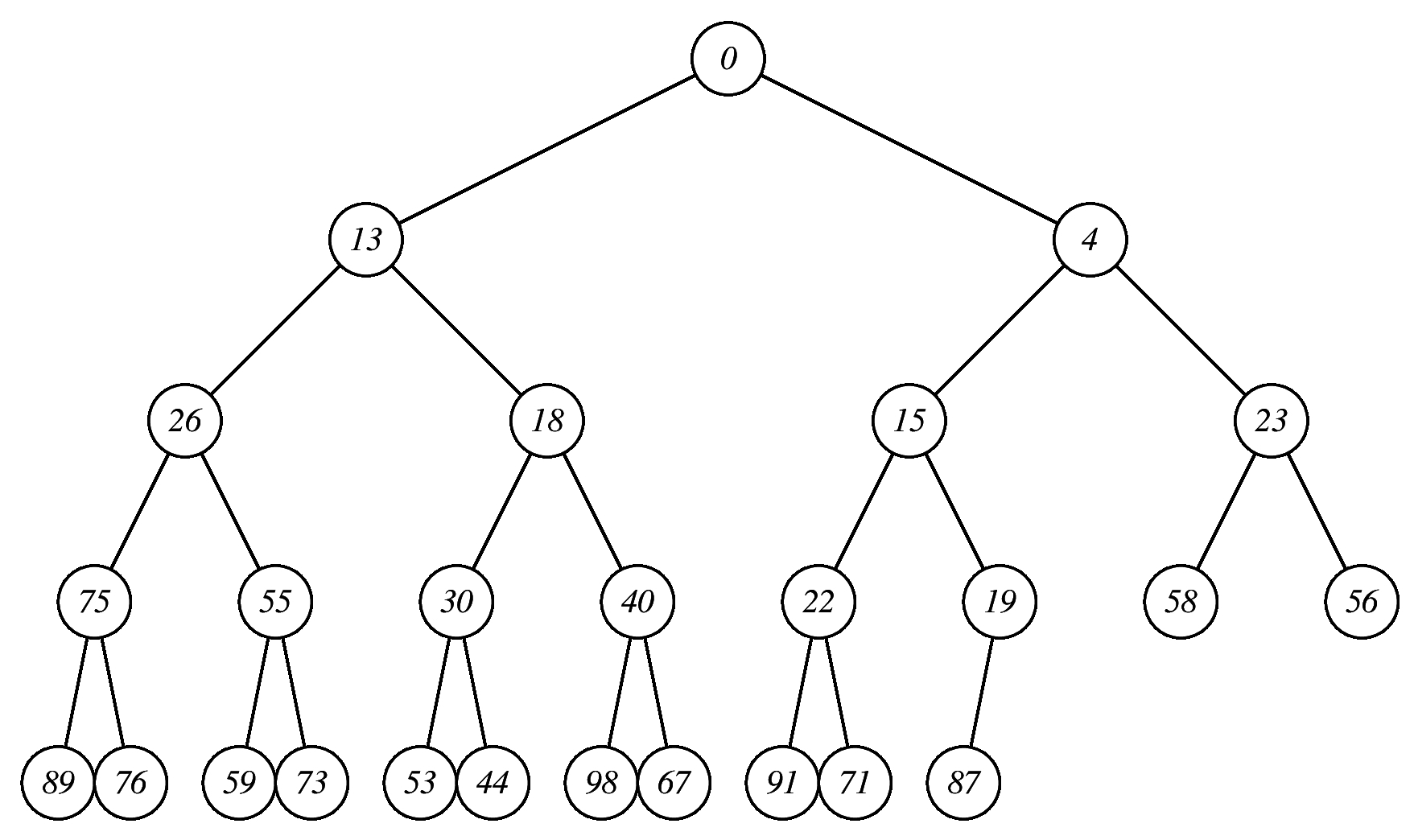To answer the question, simply find each value on the heap:

h[1] = 13
h[2] = 4
h[5] = 15
h[6] = 23
h[11] = 22
h[12] = 19
h[24] = 71
h[25] = 81

To find your question, look at the name of the person. Here are the questions, answers, and heaps for each of the people:

Jacob: Questions, Answers, Heap.
Brooke: Questions, Answers, Heap.
Savannah: Questions, Answers, Heap.
Logan: Questions, Answers, Heap.
Riley: Questions, Answers, Heap.

Grading

Each question was worth 1.5 points. On your grade, your answers are recorded as:

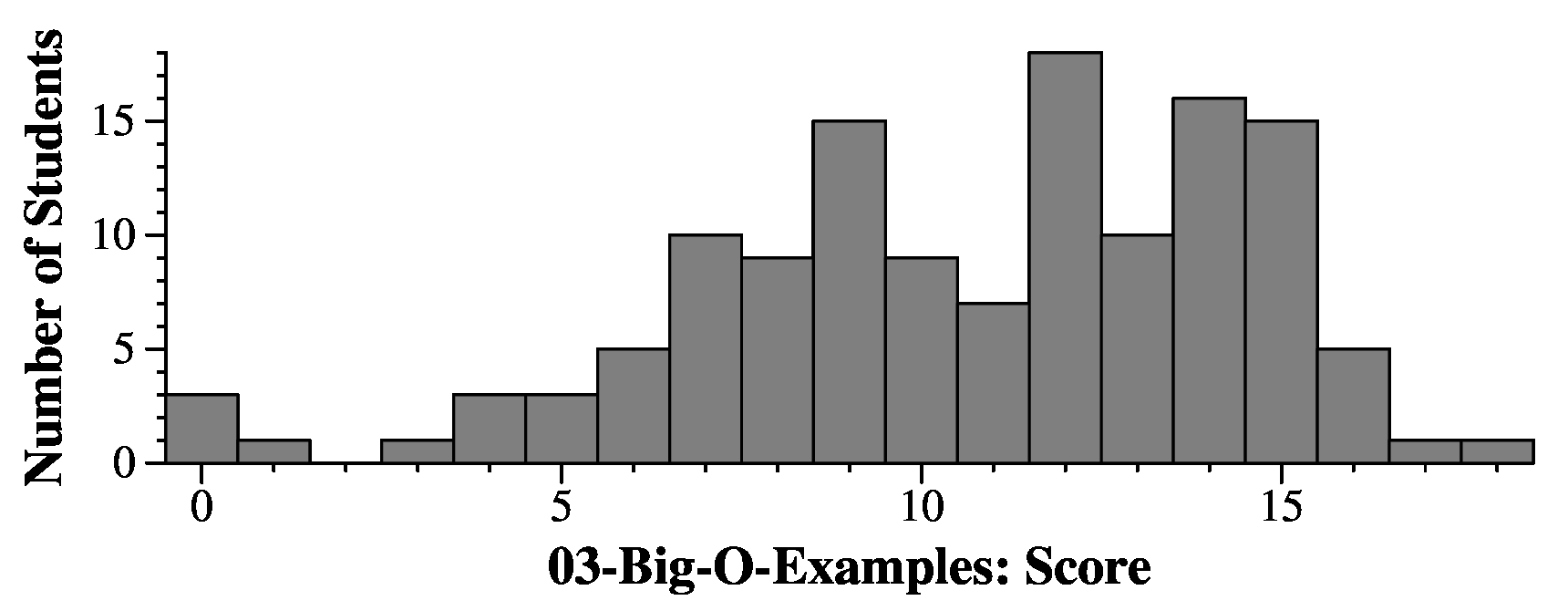
Initial-Q#-Iindex-your-answer

The Initial is J, R. L, B, S for Jacob, Riley, Logan, Brooke and Savannah. So, for example, if your answer is recorded as B-Q1-I1-17, you interpret that as "Brooke, question 1, looking for h[1], and you answered 17."

I gave partial credit of 0.5 points for each of the following:

B-Q1-I1-43
B-Q1-I1-9
B-Q2-I2-17
B-Q2-I2-19
B-Q2-I2-72
B-Q3-I5-25
B-Q3-I5-39
B-Q3-I5-40
B-Q3-I5-85
B-Q3-I5-87
B-Q4-I6-19
B-Q4-I6-31
B-Q4-I6-39
B-Q4-I6-43
B-Q4-I6-49
B-Q4-I6-59
B-Q5-I10-53
B-Q6-I11-47
B-Q7-I23-92
B-Q8-I24-14
B-Q8-I24-55
B-Q8-I24-58
J-Q1-I1-8
J-Q2-I2-10
J-Q2-I2-16
J-Q3-I5-24
J-Q4-I6-18
J-Q5-I11-52
J-Q6-I12-41
J-Q7-I24-82
J-Q8-I25-99
L-Q1-I1-0
L-Q1-I1-89
L-Q2-I2-13
L-Q2-I2-15
L-Q3-I5-18
L-Q3-I5-19
L-Q4-I6-73
L-Q6-I12-87
L-Q7-I24-91
L-Q8-I25-4
L-Q8-I25-71
R-Q1-I1-1
R-Q1-I1-4
R-Q2-I2-6
R-Q2-I2-7
R-Q3-I5-28
R-Q3-I5-8
R-Q4-I6-7
R-Q5-I11-11
R-Q6-I12-43
R-Q7-I24-77
R-Q8-I25-52
S-Q1-I1-5
S-Q2-I2-12
S-Q2-I2-39
S-Q3-I5-17
S-Q4-I6-57
S-Q5-I11-40
S-Q6-I12-60
S-Q7-I24-79
S-Q7-I24-88
S-Q8-I25-67
S-Q8-I25-68
S-Q8-I25-91

Questions 3-14

These came from a bank and were randomly ordered. Here they are:

What is the Big-O running time of inserting the value 100 n times into an empty set of integers? O(1). Sets don't insert duplicates, so the set size is always 1.
What is the Big-O running time of inserting n integers in the front of a vector with n elements? O(n²)
What is the Big-O running time of finding a value in an AVL tree with n elements? O(log n)
Suppose that there are m unique elements in a multiset with n elements. What is the Big-O running time of printing all of those unique elements? O(n) -- that's how long it takes to traverse the multiset. I also gave credit to O(m log n), which you can achieve using upper_bound. We'll learn more about that next semester.
What is the Big-O running time of creating a sorted vector from an AVL tree with n elements? O(n) - Tree traversal.
What is the Big-O running time of given an iterator into a map with n elements, calling erase() on that iterator? O(log n)
What is the Big-O running time of creating a heap from a vector with n elements? O(n) - That's what's special about a heap.
What is the Big-O running time of removing the minimum element from a heap with n elements? O(log n)
What is the Big-O running time of dividing an integer n by 2 until it equals zero? O(log n)
What is the Big-O running time of inserting n values into an empty multimap? O(n log n)
What is the Big-O running time of inserting n values repeatedly in front of the 3rd element in a list that starts with n elements (and n > 3)? O(n). It's O(1) to get to the 3rd element, and O(1) for each insertion.
What is the Big-O running time of inserting n values repeatedly in front of the 1st element in a deque with n elements? O(n). push_front() on a deque is O(1).

Grading

Each question was worth 1.5 points.

Question 15

These came from a bank. Here's an example:

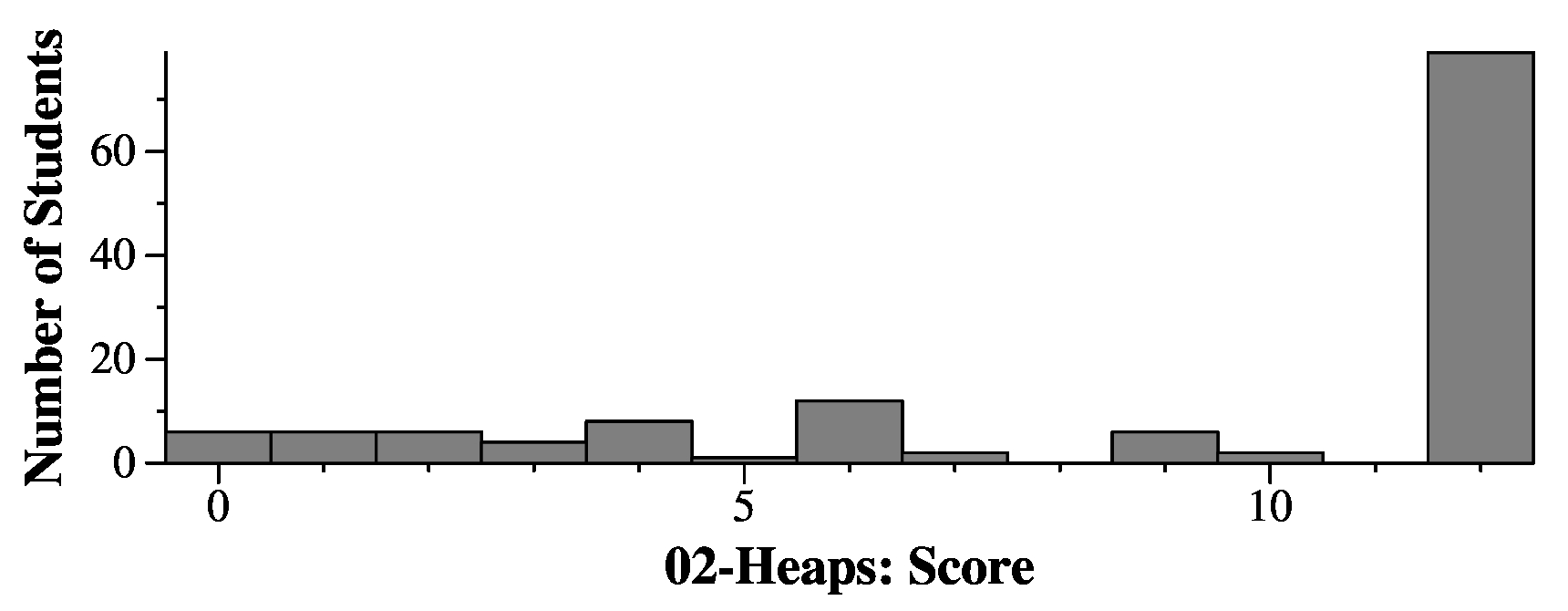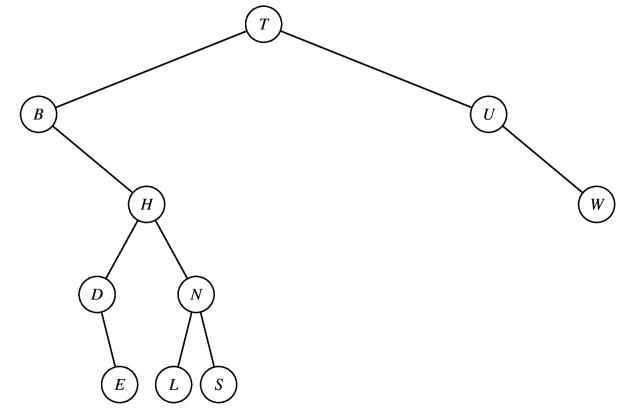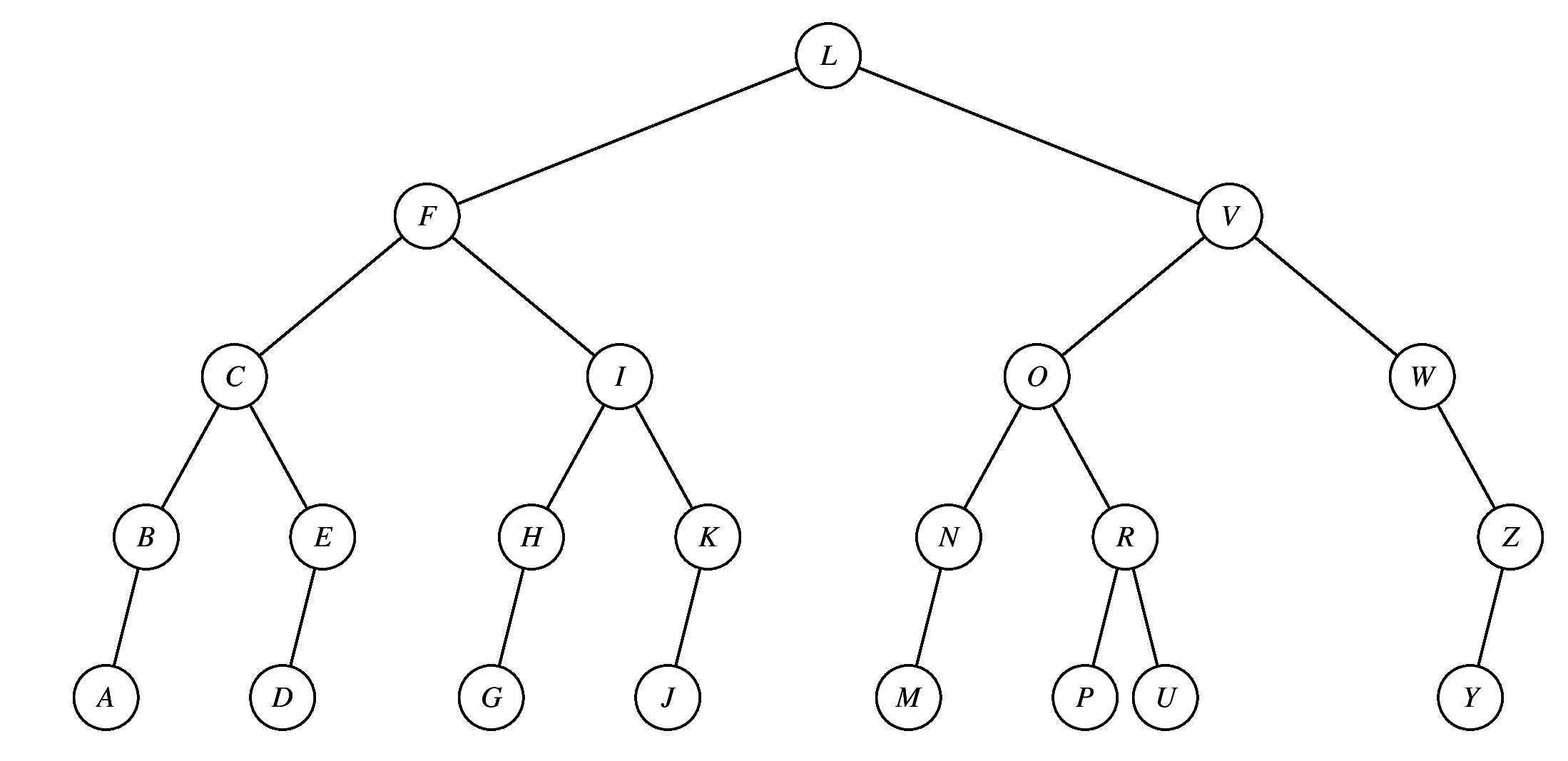
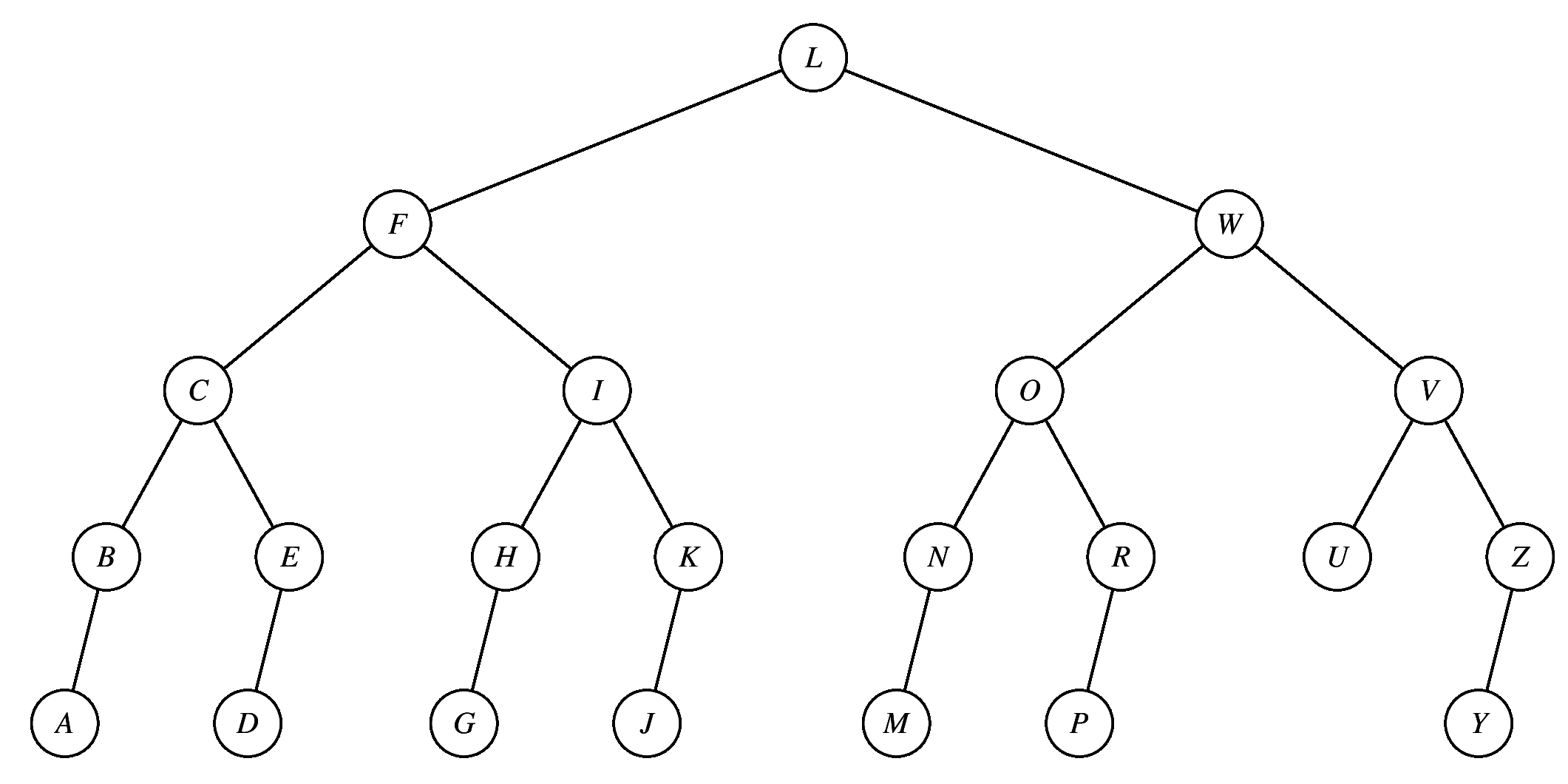
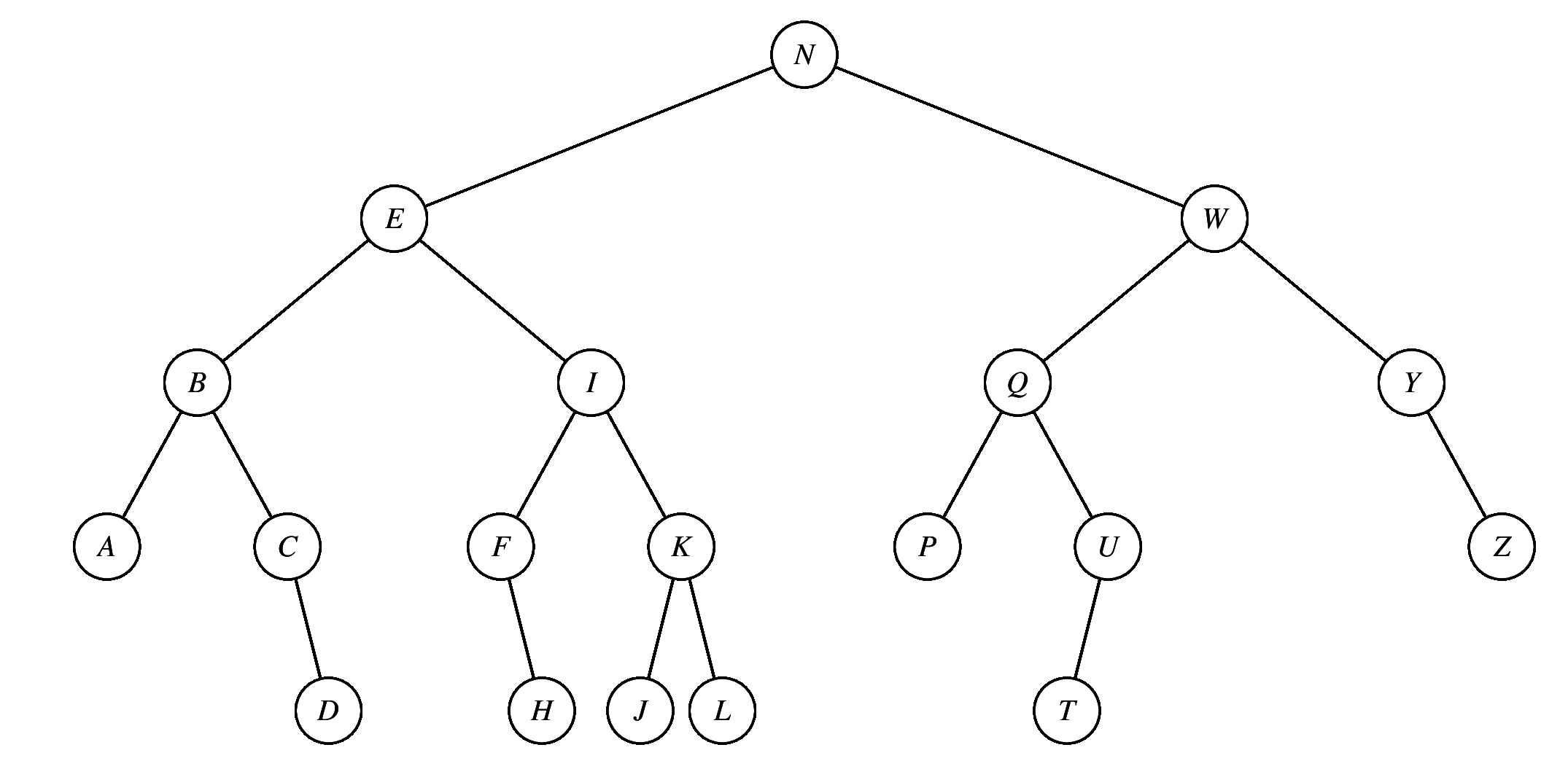
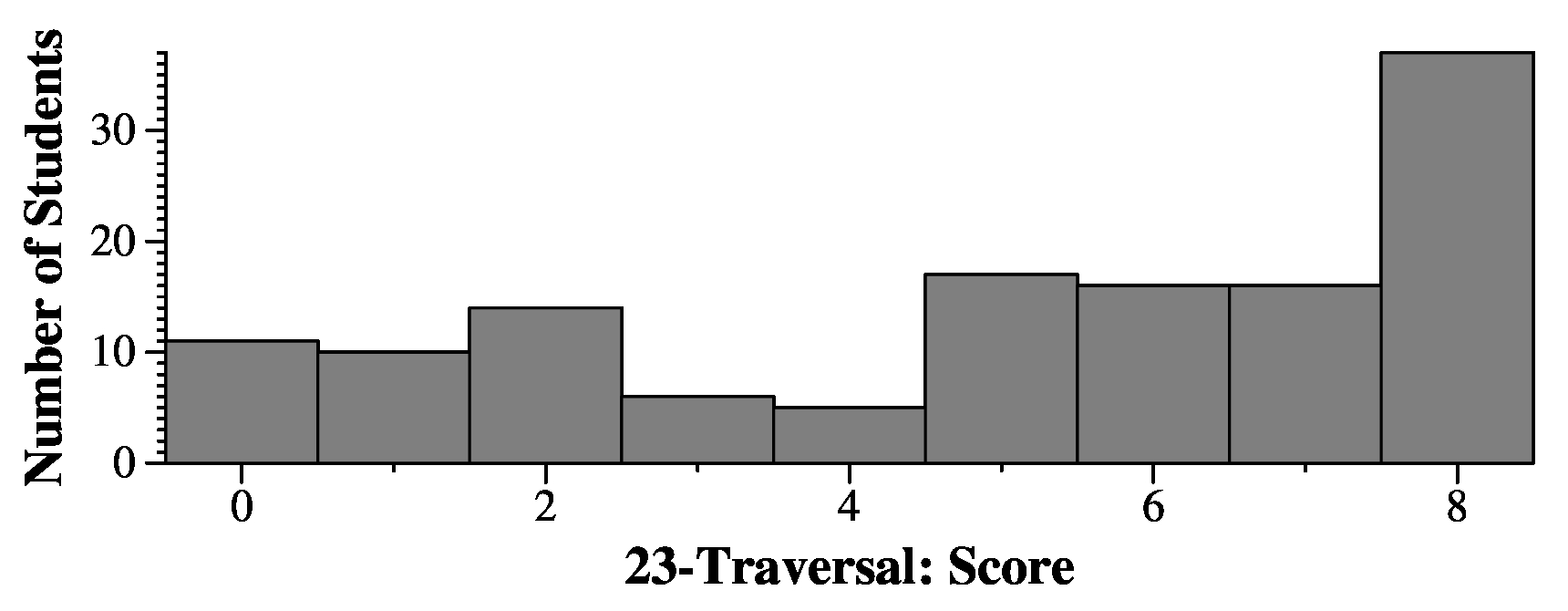
In the following blank, please enter a preorder printing of the nodes. You can just enter all of the letters, in order, without spaces: TBHDENLSUW

And in the following blank, please enter a postorder printing of the nodes: EDLSNHBWUT

Grading

Each traversal was worth 4 points. To see your tree, your question had a six character hash -- here are the trees corresponding to the hashes:

In your grading file, each of your traversals are represented in the form "X-Y", where X is the correct traversal, and Y was your traversal. Obviously, if X and Y matched, you got full credit. Here's partial credit for the preorder traversals:

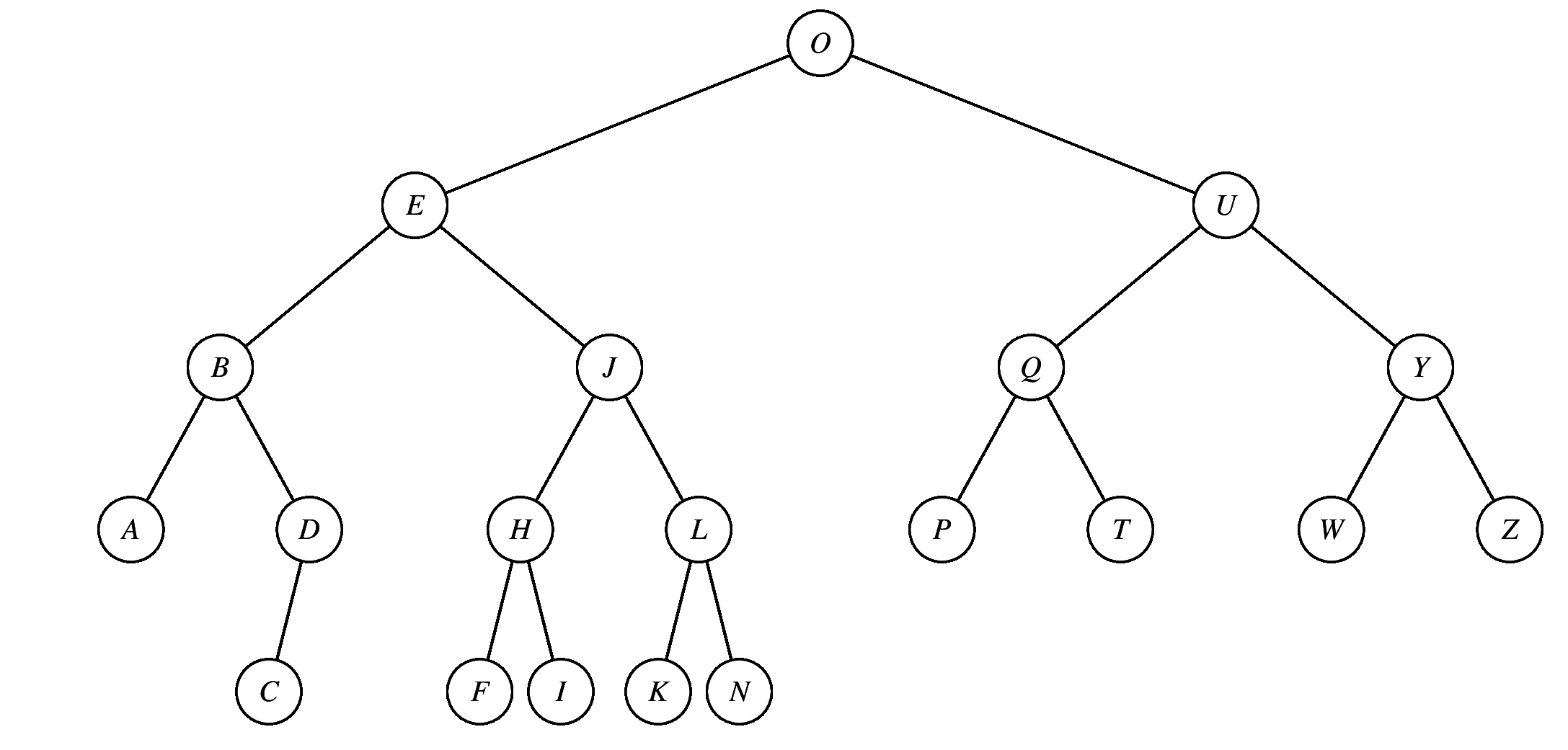
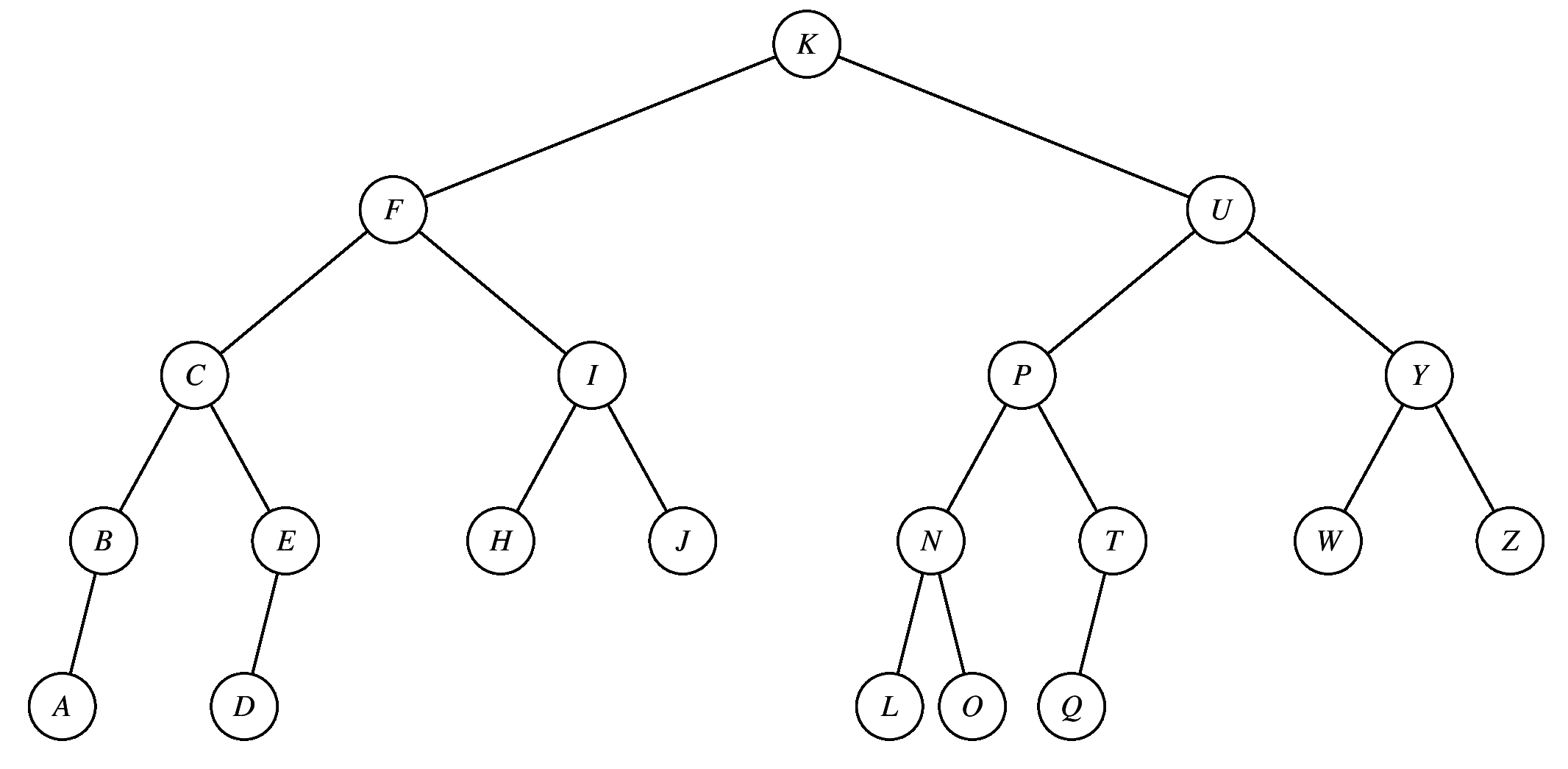
Points  Traversal
 3.5    OJDBMUSTZW-OJDBMUSTZX
   3    TBHDENLSUW-TBHDENLS
   3    HEADCGZOKU-HEAGDCZOKU
   3    DBAGFERJQS-DBGAFREJSQ
   3    DBAGFERJQS-DBAGFERJSQ
 2.5    HEADCGZOKU-HEGADCZOKU
   2    DBAGFERJQS-ABEFQJSRGD
 1.5    VDCANIFUPY-VDCNAIUFP

And here's partial credit for the postorder traversals:

 3.5  ABEFQJSRGD-ABEFQJRSGD
   3  EDLSNHBWUT-EDLSNHWBUT
   3  BDMJTSWZUO-BDMJSTWZUO
   3  BDMJTSWZUO-BDMJOTSWZU
   3  ACFIPUNDYV-ACFIPUNYV
   2  ABEFQJSRGD-DBAGFERJQS
   1  EDLSNHBWUT-EDHLNSBTWU
   1  EDLSNHBWUT-EDHLNSBTUW
   1  CDAGEKUOZH-CDAGKUOEZH
   1  BDMJTSWZUO-BDJOMTSUWZ
   1  BDMJTSWZUO-BDJMTSWZUO
   1  BDMJTSWZUO-BDJMOTSUWZ
   1  ACFIPUNDYV-ACDFINPUVY
   1  ABEFQJSRGD-ABDGFRSJEQ
   1  ABEFQJSRGD-ABDEFQJSRGD
   1  ABEFQJSRGD-ABDEFGQJRS
   1  ABEFQJSRGD-ABDEFGJQRS

Question 16

These came from a bank. Here's an example:

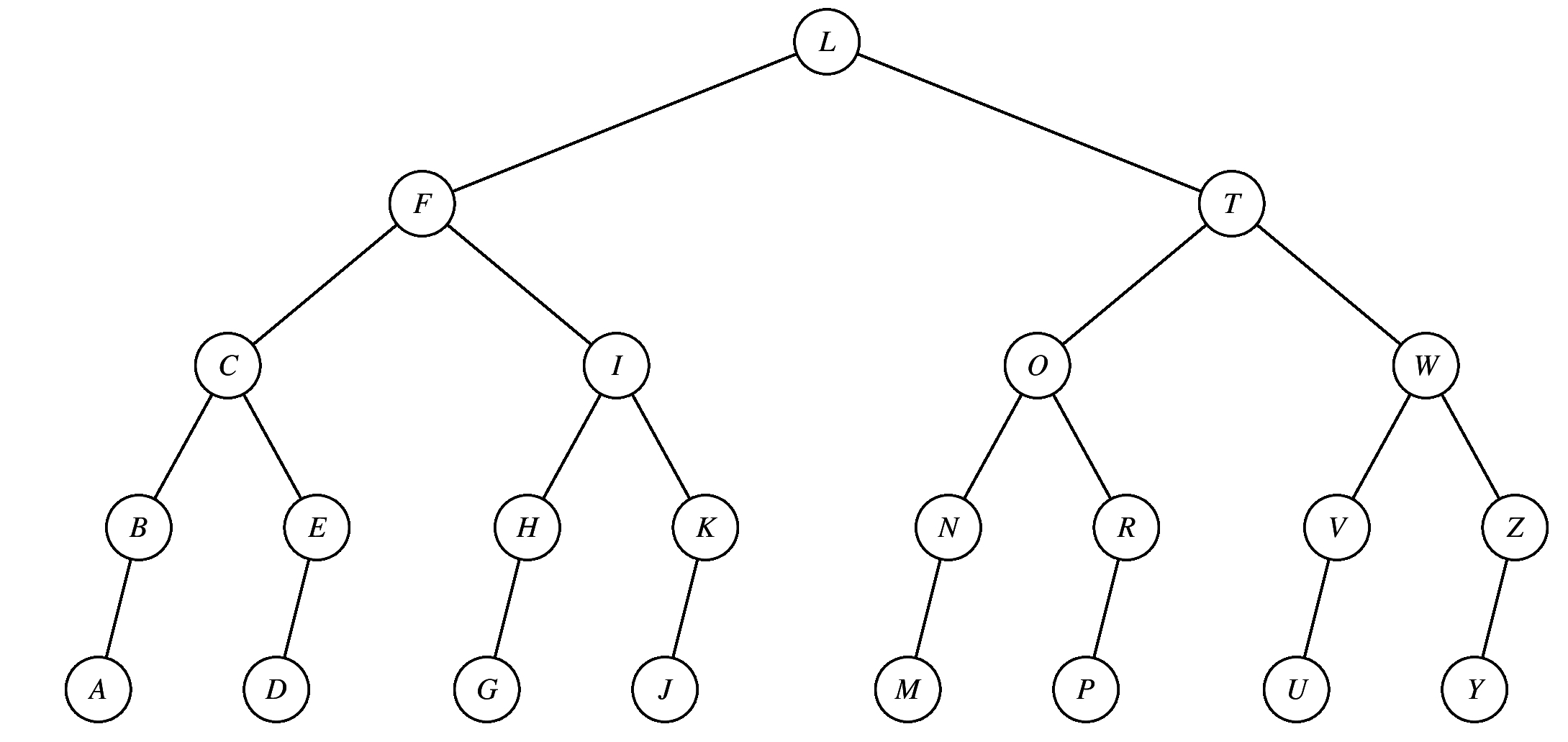In the given binary search tree, which of the following trees results when you delete the node T?

The answer is below -- you replace T with R and delete R.

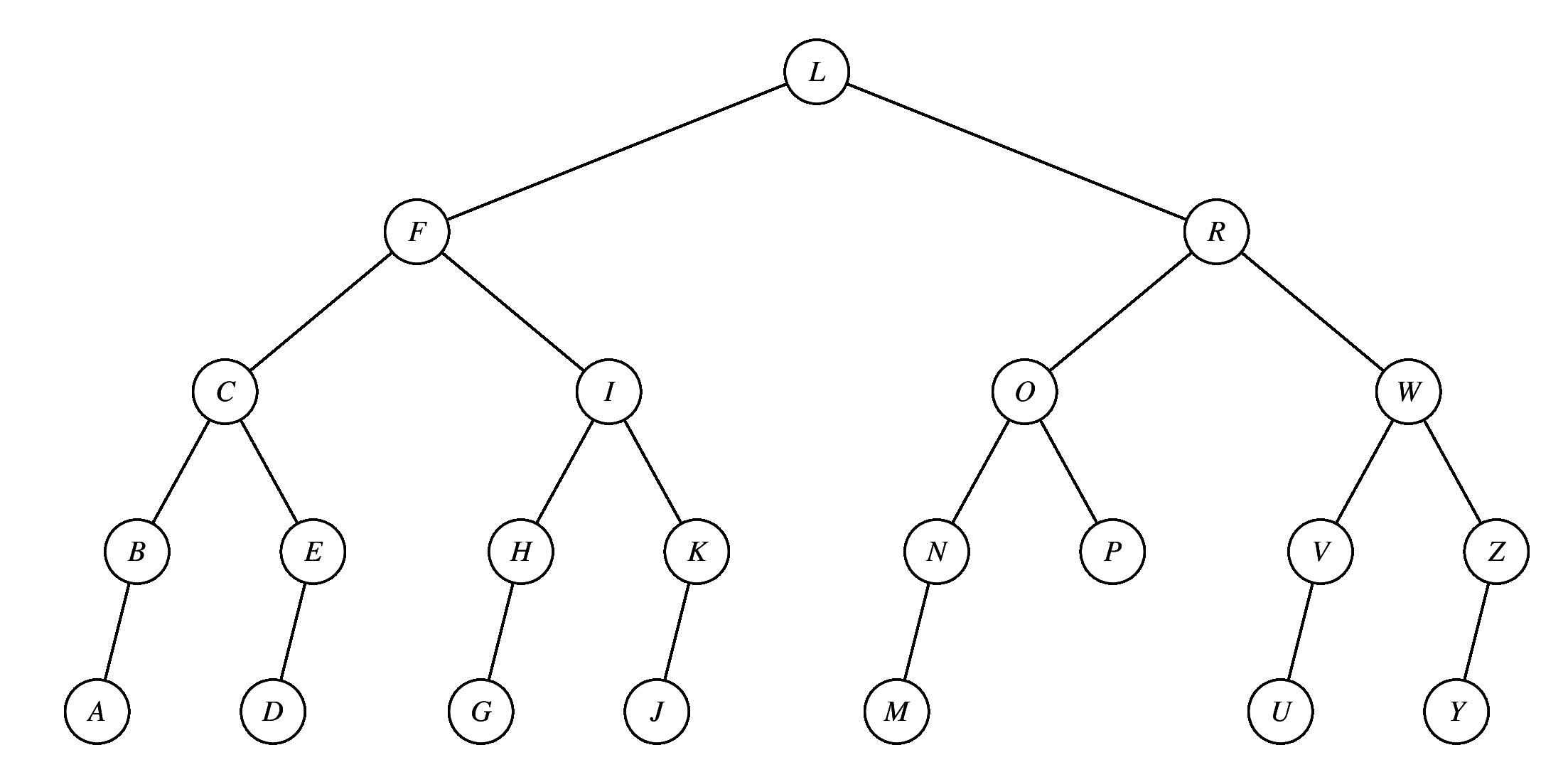This was a multiple choice question. The following answers were incorrect (if you click on them, you'll see them in full res).



	-

Grading

This was worth 6 points, with no partial credit. In your exam, you'll see that every picture of a tree has a four-digit hexadecimal tag. In the grading of your exam, your answer is labeled with three tags. The first is the picture of the binary search tree in the question, the second is the answer, and the third is your answer. Your answer is only correct if the second and third tags match.

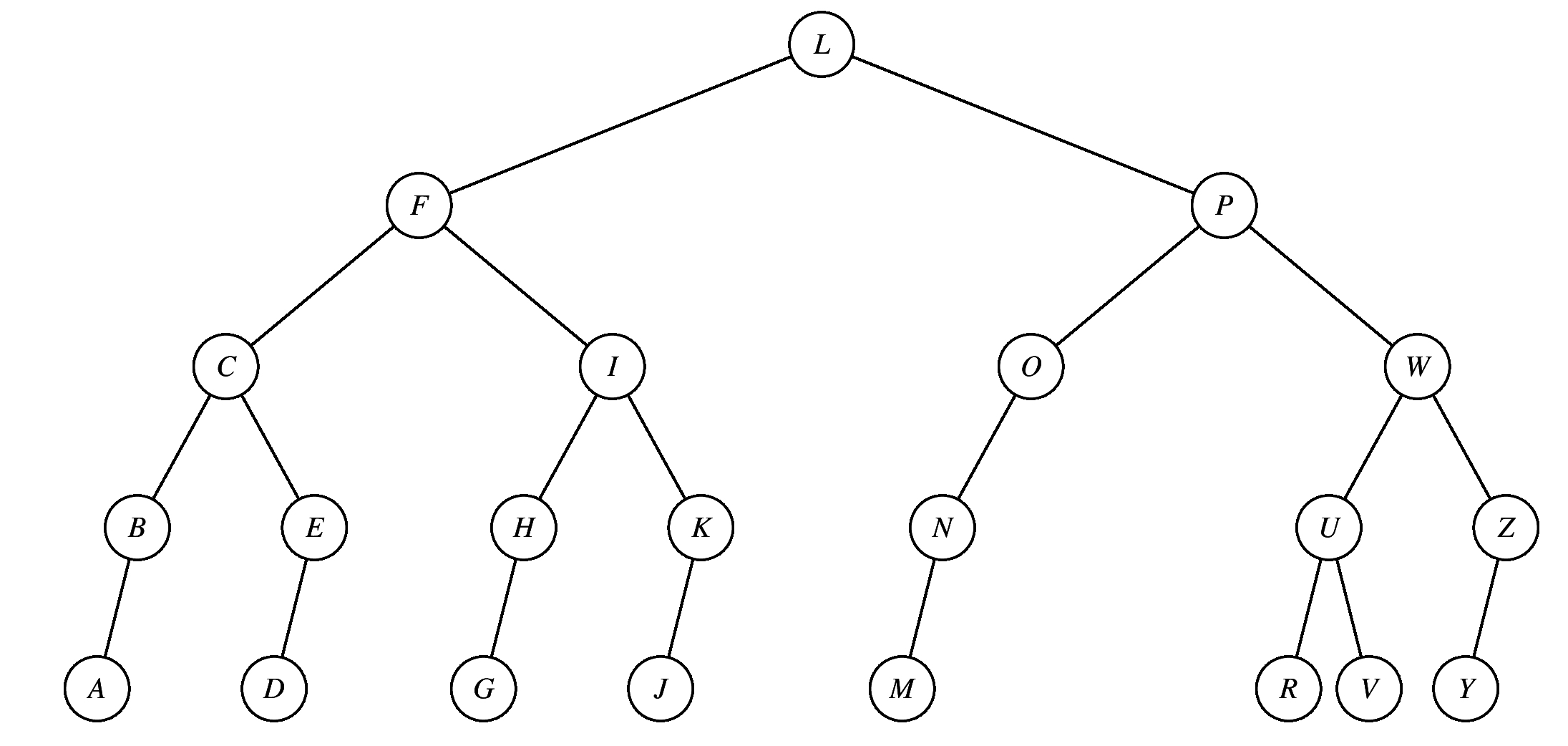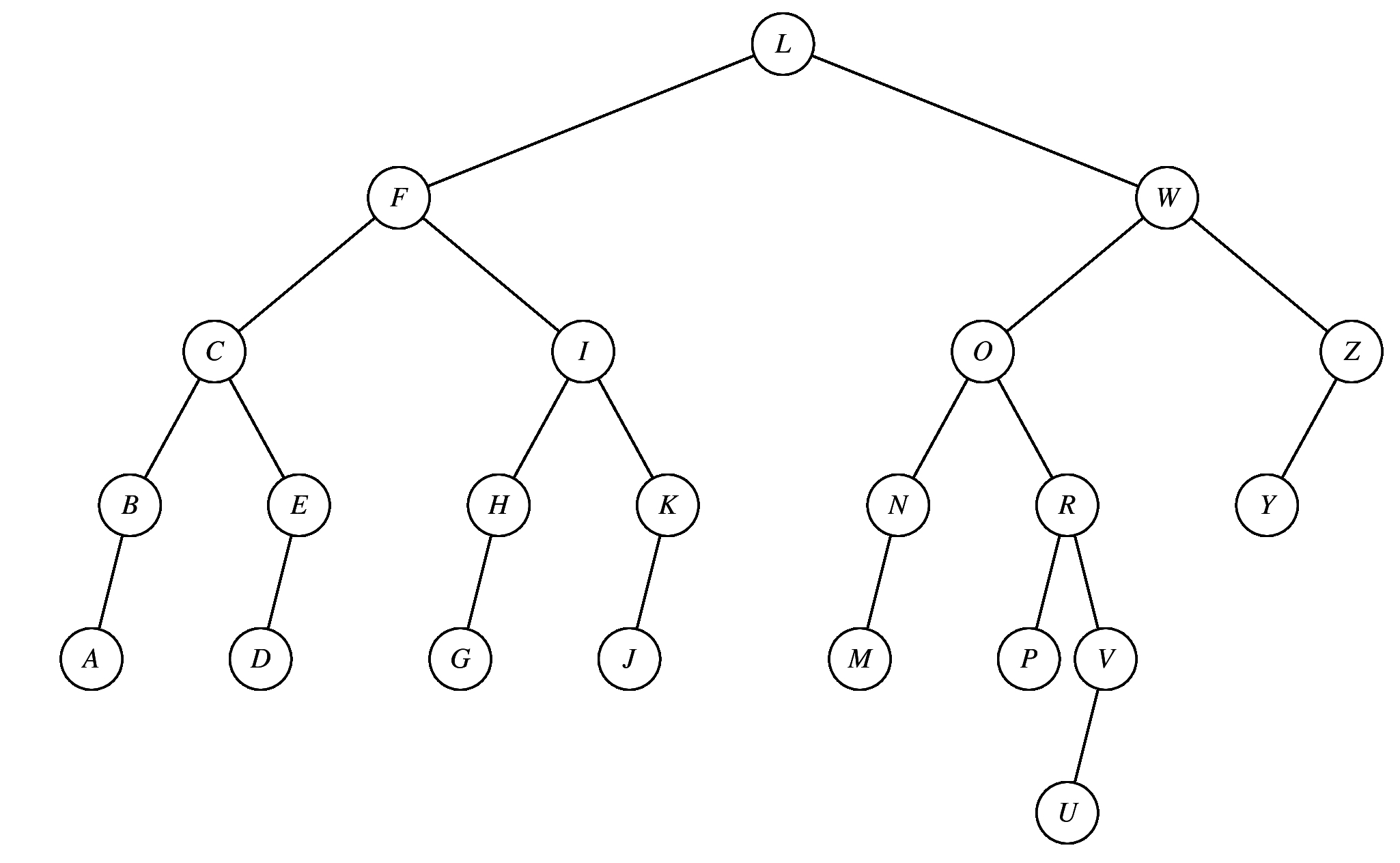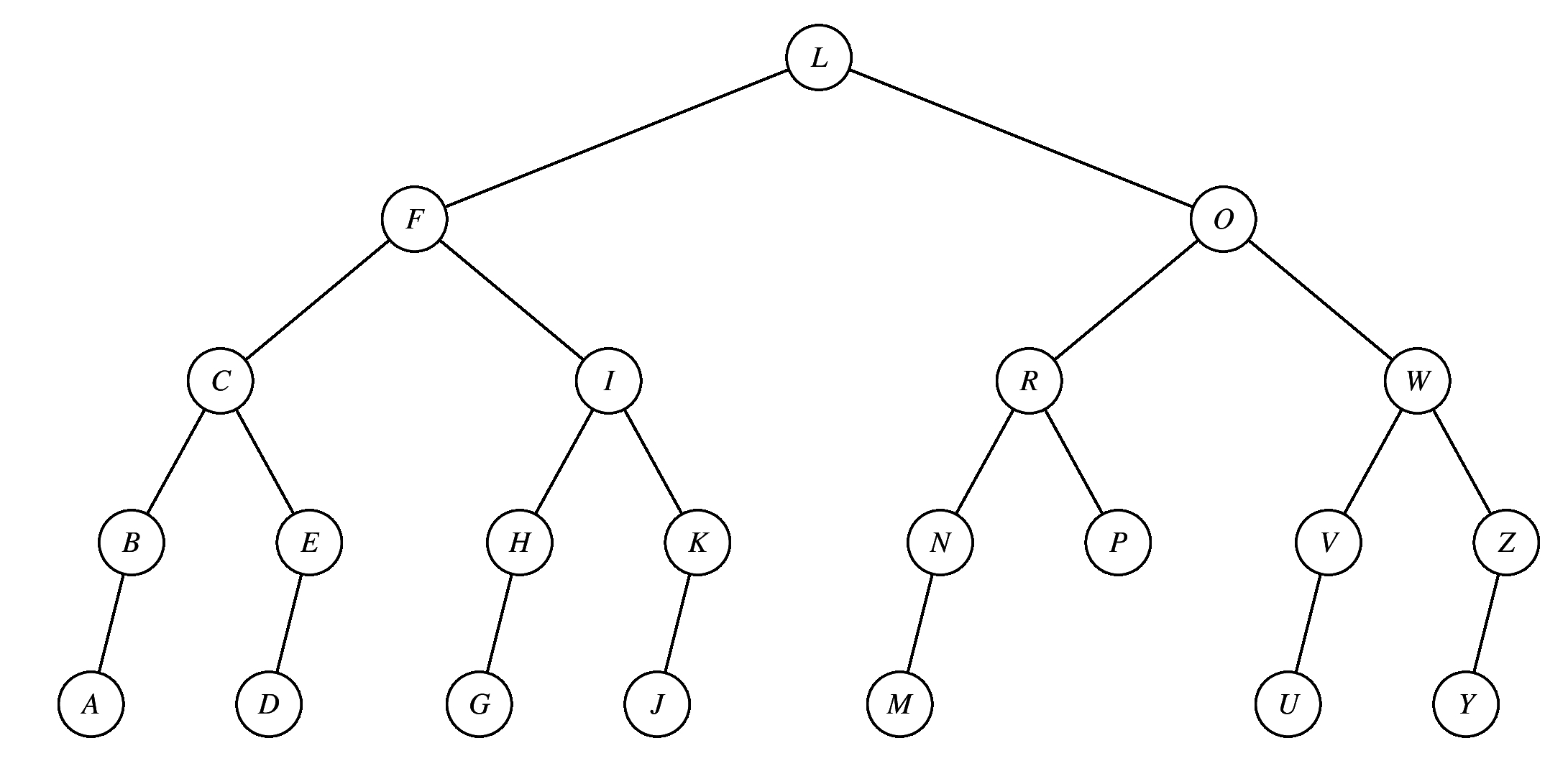Below are all of the tags with links to their pictures, so that you can see your question and answer:

Questions 17 through 20

These were given in a random order:

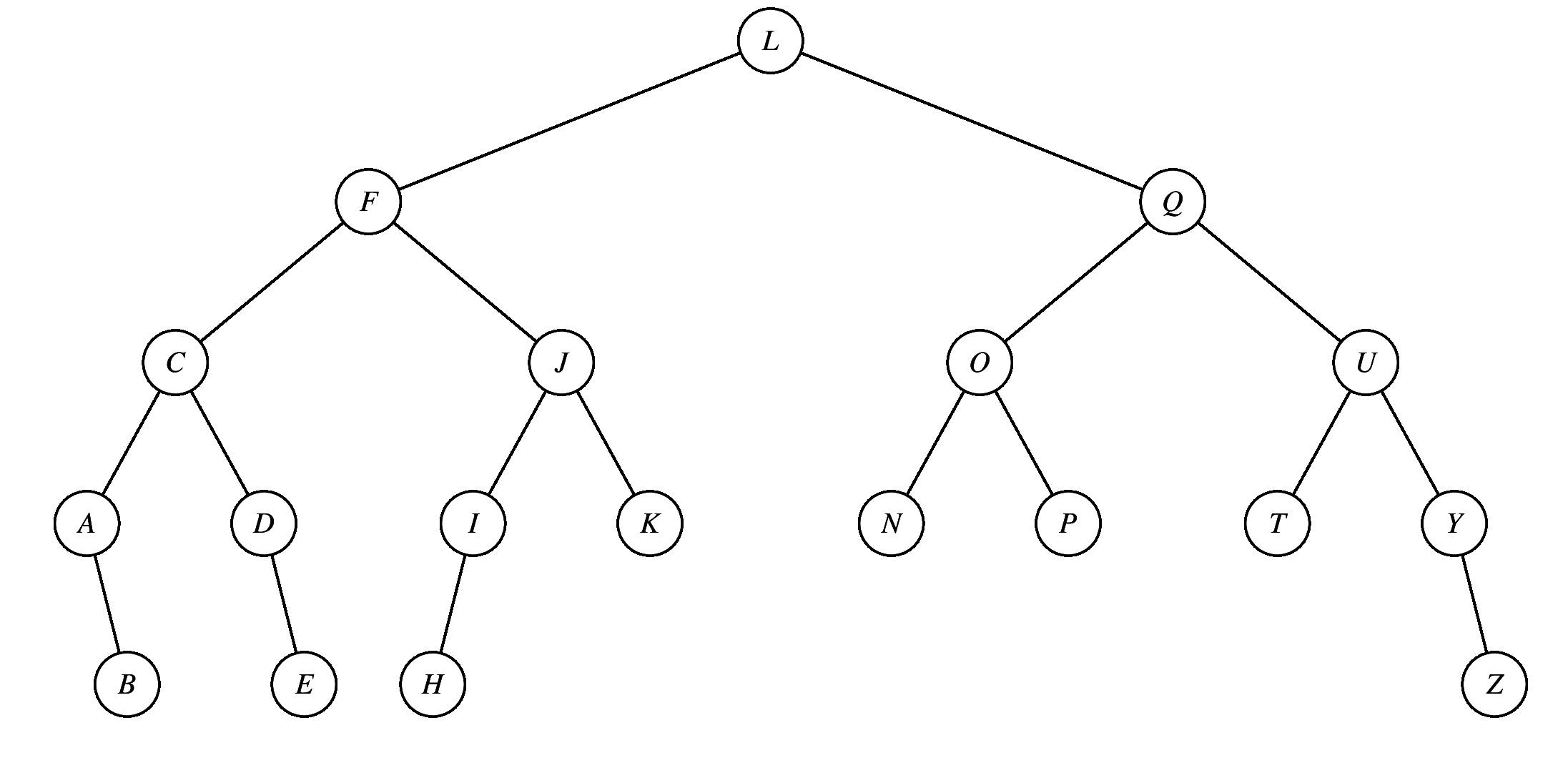
(f9f1) Suppose you insert M into the AVL tree above. The first rotation will be about the node _________. How many total rotations will there be? _________.

Answers: J, 2.

(6f57) Suppose you insert M into the AVL tree above. The first rotation will be about the node _________. How many total rotations will there be? _________.

Answers: P, 1.

(3e0a) Suppose you delete T from the AVL tree above. The first rotation will be about the node _________. How many total rotations will there be? _________.

Answers: Y, 1.

(7d26) Suppose you delete Y from the AVL tree above. The first rotation will be about the node _________. How many total rotations will there be? _________.

Answers: U, 2.

Grading

4 points per question. I gave some partial credit, when, for example you had the right node but the wrong number of rotations.

Question 21

You have the following class definition in zippy.hpp:

class Zippy {
  public:
    Zippy();
    ~Zippy();
    Zippy(const Zippy &z);
    Zippy& operator= (const Zippy &z);

    Do_Stuff(const vector <int> &stuff);
    vector <int> Get_Stuff() const;
  protected:
    void *s;
};

In zippy.cpp, you have the following class definition:

class MyZippy {
  public:
    vector <int *> v;
};

Here's the constructor for Zippy:

Zippy::Zippy()
{
  MyZippy *z;

  z = new MyZippy;
  s = (void *) z;
};

I'm not going to show you any method implementations, but I'll tell you that Do_Stuff() makes multiple calls of the form "z->v.push_back(new int)". Please write the destructor. (Remember to set the entry box's "paragraph" to "preformatted").

Answer

The destructor needs to typecast s to an instance of MyZippy *. Then it should delete any integers allocated in the vector. Finally, it should delete the instance of MyZippy *. You don't need to clear the vector, because that is done automatically in the last delete call:

Zippy::~Zippy()
{
  size_t i;
  MyZippy *z;

  z = (MyZippy *) s;
  for (i = 0; i < z->v.size(); i++) delete z->v[i];
  delete z;
}

Grading

Typically you started with 8 points and then had deductions. Common deductions:

You used z, but didn't set it to be (MyZippy *) s: -3
You used z, but then did "delete s" or "delete z->s": -1
You didn't use z at all, but pretended that Zippy had a vector v, and then you typically deleted s: -4.
You forgot to delete z (or s): -1 or -2, depending on the other things in your program.

Question 22

Recall the following class definitions from dlist.hpp:

class Dnode {
  friend class Dlist;
  public:
    std::string s;
    Dnode *Next();
    Dnode *Prev();
  protected:
    Dnode *flink;
    Dnode *blink;
};

class Dlist {
  public:
     /* A bunch of stuff that doesn't matter. */

    Dnode *Begin() const;         // Pointer to the first node on the list
    Dnode *End() const;           // Pointer to "one past" the last node on the list.

    void Insert_Before(const std::string &s, Dnode *n);

  protected:
    Dnode *sentinel;
    size_t size;
};

Implement these three methods. You cannot call any other methods of Dlist, and you cannot call the Next() or Prev() methods of the Dnode class.

Answer

Dnode *Dlist::Begin()
{
  return sentinel->flink;
}

Dnode *Dlist::End()
{
  return sentinel;
}

void Dlist::Insert_Before(const string &s, Dnode *n)
{
  Dnode *newnode, *prev;

  newnode = new Dnode;
  prev = n->blink;

  newnode->s = s;
  newnode->flink = n;
  newnode->blink = prev;   // this could be newnode->blink = n->blink; 
  n->blink = newnode;
  prev->flink = newnode;   // this could be newnode->blink->flink = newnode;
  size++;
}

Grading

Typically, you started with 10 points, and then had deductions. Common deductions:

Begin() implemented incorrectly: -1
End() implemented incorrectly: -1
s not set: -1
size not incremented: -1
newnode->flink set incorrectly: -1.5
newnode->blink set incorrectly: -1.5
n->blink set incorrectly: -1.5
prev->flink set incorrectly: -1.5
Didn't call new to allocate memory for newnode: -1.5
Loops: At least -3

Question 23

Below is the class definition of a node in a tree:

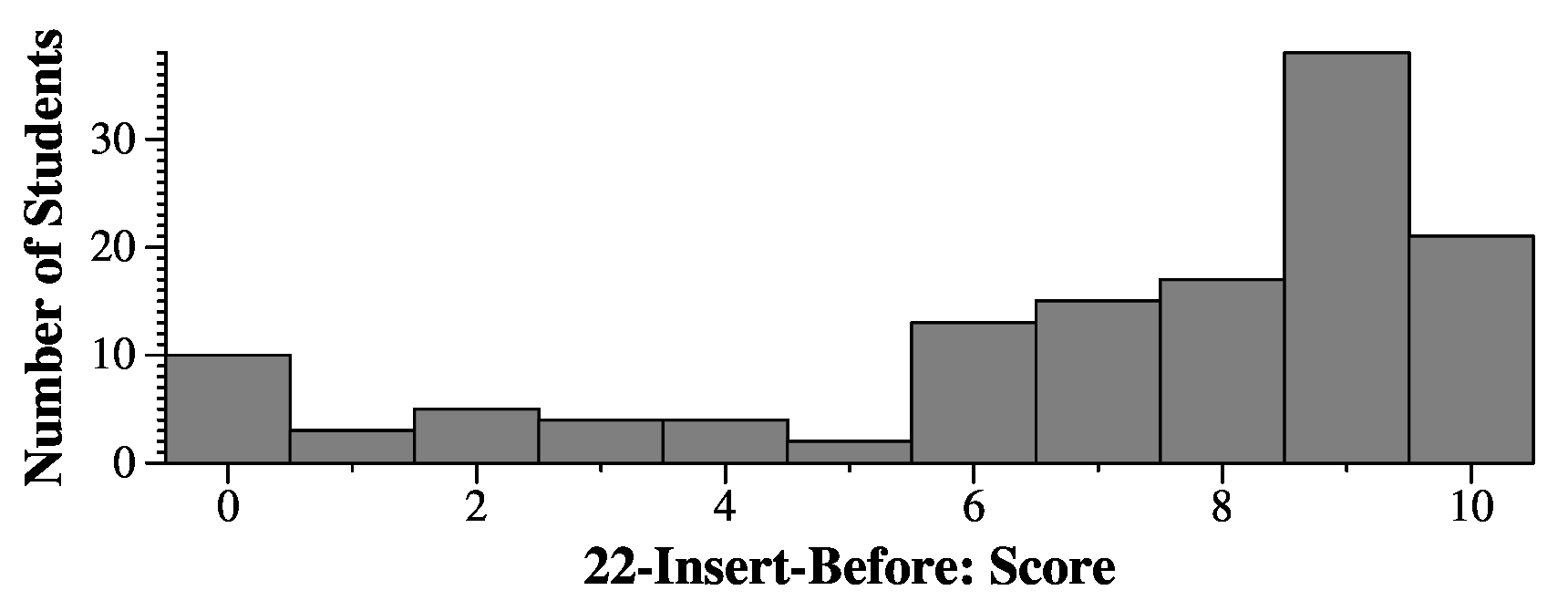class TreeNode {
  public:
    vector <TreeNode *> children;
    double weight;
};

Let's define a "rank" of a subtree rooted by a node to be the maximum of the node's weight, and the average rank of the subtrees rooted by the node's children. Please write a procedure with the following prototype, that returns the rank of a node's subtree:

double rank(const TreeNode *n);

Answer

The answer is a straightforward postorder traversal:

double rank(const Treenode *n)
{
  double total, average;
  size_t i;
  
  /* Base case is when a node has no children. */

  if (n->children.size() == 0) return weight;

  /* Otherwise, compute the average rank of the children. */
  total = 0;
  for (i = 0; i < n->children.size(); i++) {
    total += rank(n->children[i]);
  }
  average = total / (double) n->children.size();
 
  /* Return tha maximum */
  return (weight > average) ? weight : average;
}

Grading

There were at least ten questions during the exam with students being confused about the definition of "rank". And several students made remarks on their exams that they didn't understand the definition. I ran the question by Dr. Vander Zanden after the exam, and he said it was "crystal clear", and that he suspects, as I do, that the confused students are not comfortable with recursion, as the definition is recursive.

So for the students who were confused, and to any students studying from this exam, please make yourself comfortable with this definition. It's a tree, so there will be internal and external nodes. External nodes have no children, so the rank here is the node's weight. That's the base case of the recursion, and without it, the definition of "rank" would be circular and incomplete. With internal nodes, you recursively call rank() on the children, and then calculate the average. The rank is then the maximum of that and the node's weight.

Grading here went one of two ways. If your code was confused, you simply received a point or two, depending on how confused it seemed. If it wasn't confused, then you started with 8 points and received deductions. Here were the common deductions:

Division by zero (you didn't account for n->children.size() being zero: -2.
Not initializing the total while computing the average: -1.
Not using "n->" and instead treating children like you were implementing a method of TreeNode: -1.
Calculating the average incorrectly: -2

Question 24

Behold the following program:

#include <iostream>
#include <vector>
using namespace std;

void a()
{
  int i;
  vector <int> v;

  while (cin >> i) {
    v.push_back(i);
    if (i%2 == 0) a();
  }
  for (i = 0; i < v.size(); i++) cout << " " << v[i];
}

int main()
{
  a();
  cout << endl;
  return 0;
}

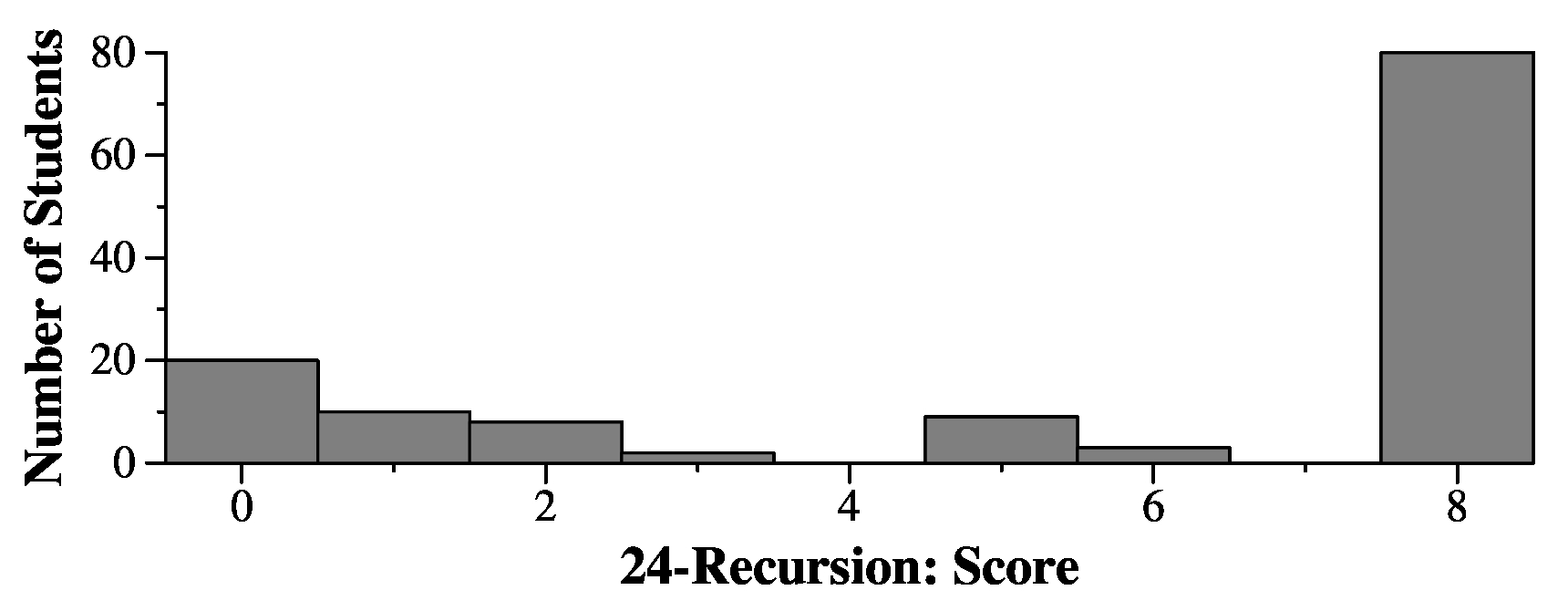
Suppose that this is compiled to a.out.In line one of your answer below, please put the output to:

echo 10 11 12 | ./a.out

In line two of your answer below, please put the output to:

echo 91 50 19 97 84 88 68 | ./a.out

Please answer in the proper format. Which means that line one contains the output of the first call, and line two contains the output of the second call. If you want to put other stuff in your answer, please put it after those first two lines.

Answer

11 12 10
68 88 19 97 84 91 50

Grading

4 points per output. Partial credit: 1 point for answers that begin with the right number, and 1 point for answer that have the proper numbers, none repeated, in the wrong order.