 |
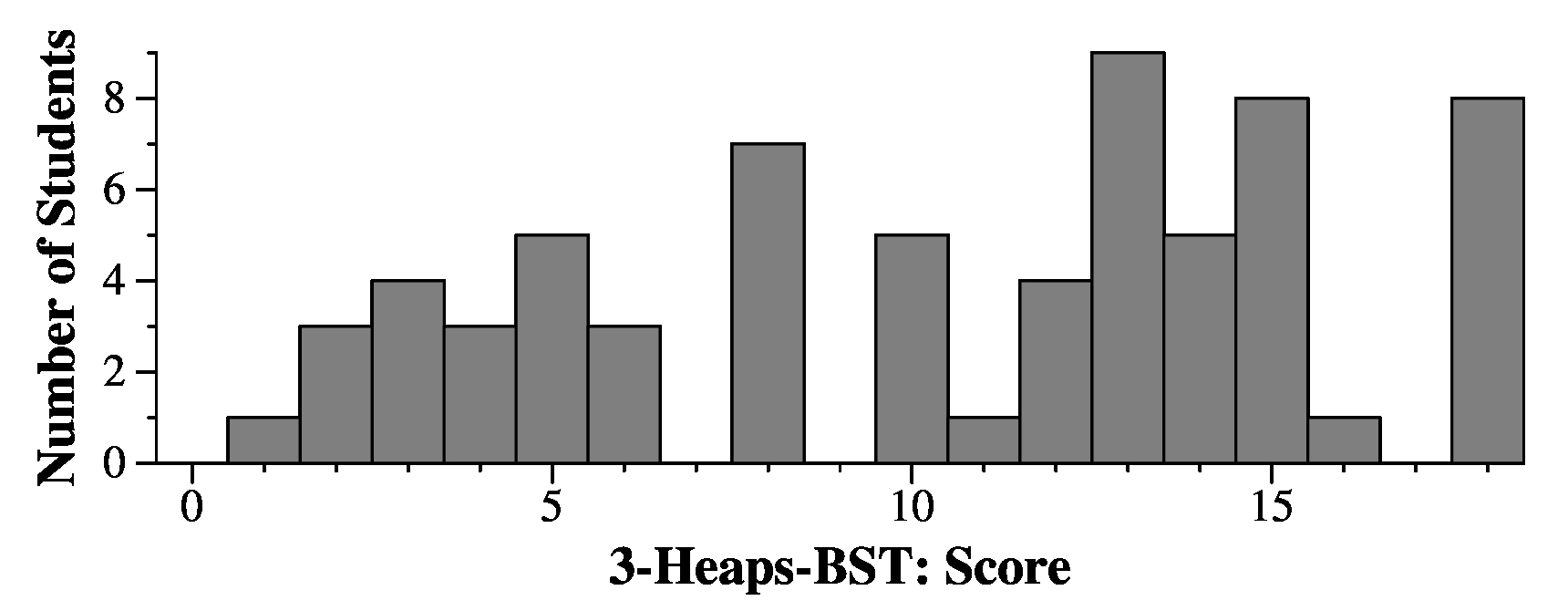
The last value of the vector will be 44, which was swapped into the last value when you did the percolate-up on 38.
When you call Pop() on the heap, 14 will be returned, and 33 will be moved onto the root. You then percolate down. You will swap 33 with 15 (index 2), then with 24 (index 6), and then you stop, because the next two children are 67 and 66. The answer is 6.
The first value will be 15, because you swapped 33 with 15 as the first step of percolating down.
LFN will go between JRC and LPH. LPH has a left child already, so it will have to be the right child of JRC. The answers are "JRC" and "R". You could also go from the root:
Now, to match correct answers, for the first part, look in your exam that I sent in your "grappling hook". It will show the filename of the JPG for the heap picture. Look at the first five characters of that filename. Here are correct answers to the first question:
5dae0-12 70e5e-11 e701c-12 e855a-10 |
And the second question:
5dae0-44 70e5e-49 e701c-74 e855a-86 |
For the remaining questions, look at the filename for the "vector form" of the heap. Again, look at the first five characters of the filename. Here are the answers to the remaining questions:
Third Question: 5dae0-6 64fb3-6 70e5e-6 e701c-6 e855a-4 |
Fourth Question: 5dae0-15 64fb3-4 70e5e-6 e701c-5 e855a-6 |
Fifth Question: 5dae0-JRC 64fb3-OEI 70e5e-MRD e701c-YJQ e855a-GHO |
Sixth Question: 5dae0-R 64fb3-R 70e5e-R e701c-L e855a-R |
Seventh question: 5dae0-GOX 64fb3-NNJ 70e5e-JZK e701c-SHF e855a-MVL |
 |
Fred::Fred(const Fred &f)
{
v = new vector <int>;
*v = *(f.v);
}
|
Fred::Fred(const Fred &f)
{
int i;
v = new vector <int>;
for (i = 0; i < f.v->size(); i++) {
v->push_back(f.v->at(i));
}
}
|
Fred::Fred(const Fred &f)
{
v = new vector <int>;
*this = f;
}
|
If you didn't allocate v, you lost significant points, because that's the point of the copy constructor. You also lost points by doing v = f.v, because that's just copying a pointer, and will lead to the same disaster scenario as not implementing a copy constructor.
The assignment overlead needs to copy the vector too. This time, however, the vector is allocated and may have elements in it, so you have to clear it before you copy it. Here are two implementations:
Fred& Fred::operator= (const Fred &f)
{
*v = *(f.v);
return *this;
}
|
Fred& Fred::operator= (const Fred &f)
{
int i;
v->clear();
for (i = 0; i < f.v->size(); i++) {
v->push_back(f.v->at(i));
}
return *this;
}
|
I gave partial credit here, but one thing that lost you significant points was mixing types: "f = new Fred", or "v = *f".
 |
for (i = 0; i < s.size(); i++) v.push_back(s.substr(i));(In case you've forgotten, s.substr(i) returns the substring of s starting with the character at index i and going to the end of the string). Answer: The first string has n characters. The next has (n-1). And so on. So the total number of characters is O(n^2).
 |
Part A: Here the tree is simple enough to draw quickly. Here's ASCII-Art:
AWD
\
DBQ
\
JLB
|
Node AWD is imbalanced, and it's clearly a Zig-Zig, so you rotate once about DBQ:
DBQ / \ AWD JLB |
So the answers:
a->left->key: --- a->right->key: --- a->parent->key: DBQ b->left->key: AWD b->right->key: JLB b->parent->key: --- |
Part B: As I said in the exam, drawing the whole tree here is a waste of time. So instead, start with the root and its children:
RGD / \ OTC SIE 10 8 |
It's imbalanced toward OTC, so go ahead and add OTC's children:
RGD
/ \
OTC SIE
/ \ 8
NTD PRQ
8 9
|
This is Zig-Zag, so we're going to need to rotate twice about PRQ. Before we do that, let's add PRQ's children:
RGD
/ \
OTC SIE
/ \ 8
NTD PRQ
8 / \
PIH QME
|
Now let's rotate. For double rotations, I simply put PRQ as the root, have OTC and RGD be its children, and fill in the rest:
PRQ
/ \
/ \
/ \
OTC RGD
/ \ / \
NTD PIH QME SIE
|
Now I can answer the questions:
a->left->key: QME a->right->key: SIE a->parent->key: PRQ b->left->key: OTC b->right->key: RGD b->parent->key: TND -- That was RGD's original parent |
Part C: Let's do the same thing -- Draw IZY and its children:
IZY / \ FMS MGK 9 7 |
The imbalance is toward FMS, so draw its children:
IZY
/ \
FMS MGK
/ \ 7
DIB HQS
8 7
|
This is zig-zig, so rotate once about FMS:
FMS
/ \
DIB IZY
8 / \
HQS MGK
7 7
|
Now we answer questions:
a->left->key: HQS a->right->key: MGK a->parent->key: FMS b->left->key: DIB b->right->key: IZY b->parent->key: ODB -- That was RGD's original parent |
Part A: a->left->key: BLZ---- NWX---- VNG---- FJX---- AWD---- SCZ---- Part A: a->right->key: BLZ---- NWX---- VNG---- FJX---- AWD---- SCZ---- Part A: a->parent->key: BLZ-CBE NWX-TYP VNG-LDQ FJX-FXT AWD-DBQ SCZ-LJP Part A: b->left->key: CBE-BLZ TYP-NWX LDQ-ECB FXT-FJX DBQ-AWD LJP-AKU Part A: b->right->key: CBE-CBV TYP-ZNA LDQ-VNG FXT-MRJ DBQ-JLB LJP-SCZ Part A: b->parent->key: CBE---- TYP---- LDQ---- FXT---- DBQ---- LJP---- Part B: a->left->key: GZS-GEZ KDK-JKM NSY-NIL WFT-WBM RGD-QME XWH-XKZ Part B: a->right->key: GZS-IGC KDK-LDZ NSY-NZV WFT-WOD RGD-SIE XWH-YGU Part B: a->parent->key: GZS-FQR KDK-IXA NSY-OJB WFT-VSS RGD-PRQ XWH-YNU Part B: b->left->key: FQR-DKV IXA-HXP OJB-NSY VSS-VKI PRQ-OTC YNU-XWH Part B: b->right->key: FQR-GZS IXA-KDK OJB-OQZ VSS-WFT PRQ-RGD YNU-ZCC Part B: b->parent->key: FQR-KIS IXA-HGY OJB-MWM VSS-WXY PRQ-TND YNU-WVO Part C: a->left->key: YWB-YNG FDV-EGQ XAK-WRZ PFM-PCZ IZY-HQS OLL-NMI Part C: a->right->key: YWB-ZRA FDV-GGW XAK-XGG PFM-PJX IZY-MGK OLL-PAN Part C: a->parent->key: YWB-YEQ FDV-CVP XAK-XMW PFM-OZQ IZY-FMS OLL-PND Part C: b->left->key: YEQ-XUG CVP-BIX XMW-XAK OZQ-OSN FMS-DIB PND-OLL Part C: b->right->key: YEQ-YWB CVP-FDV XMW-XWN OZQ-PFM FMS-IZY PND-PXM Part C: b->parent->key: YEQ-WKH CVP-HDI XMW-YCK OZQ-ONI FMS-ODB PND-QQH |
 |
t->info = (pinfo >> 2) | t->children.size(); |
I changed it to make it less confusing, but forgot to make it "*4" instead of "*2". so the values in the printout of nodes 3, 4, 5 and 8 were wrong. I apologize if that confused you. You can ask if that's a typo in the exam. I would have fixed it then. Fortunately, it doesn't really affect much, but if you used *4 for your calculation instead of *2, you got credit.
A: set_info() is a preorder traversal. You have to calculate the info field of a node before you make the recursive call. 2 points.
B: The friend specification allows methods in the Tree class to access and modify the private and protected fields of the TreeNode class. 2 points. 1.2 points if you got it backwards or said it only allowed access to methods. 0.5 points if you were vague -- for example, here was a vague answer: "It can share the information with other, and can change or use."
C: Yes. 2 points.
D: read_from_stdin() has to call new to create TreeNode's. Therefore, your destructor has to delete the TreeNode's. 2 points. Again, vague or hand-wavy answers received 0.5 pts. For example: "The destructor will be responsible for freeing all the memory once the tree object goes out of scope."
E: 3 or 0x3.
F: 3 * 2 + 2 = 8. I gave full credit to 14 or 0xe in case you multiplied by four.
G: ((8 * 2) + 1) * 2 + 0 = 34. I gave full credit -- a point -- for all answers, since my examples didn't match the code.
H: Suppose your tree is a complete tree where all nodes but the leaves have four children. The root's info will be 4. Its child's info will be 12, or 1100 in binary. Its child's info will be 28, or 11100 in binary. Its child's info will be 111100 in binary. See the pattern? A node at a depth of d will have an info value that is (d+1) ones, followed by two zeros. info is a long long, you're going to overflow when d+3 equals 64. That's d=61. I gave full credit to 15, 16, 17, 29, 30, 31, 32, 33, 61, 62, 63, 64, 65. I gave half credit to other answers between 10 and 65.
 |
void Tree::Read_From_Stdin()
{
TreeNode *p, *c;
unordered_map <int, TreeNode *> s;
unordered_map <int, TreeNode *>::iterator sit;
int id, parent;
while (cin >> id >> parent) {
c = s[id];
if (c == NULL) {
c = new TreeNode(id);
s[id] = c;
}
p = s[parent];
if (p == NULL) {
p = new TreeNode(id);
s[parent] = p;
}
p->children.push_back(c);
}
root = s[0];
}
|
print(): Simple postorder traversal: do recursion, print spaces, call Print():
void Tree::print(const TreeNode *n, int level) const
{
size_t i;
if (n == NULL) return;
for (i = 0; i < n->children.size(); i++) print(n->children[i], level+2);
printf("%*s", level, ""); // A for loop works fine too, or resize a string with spaces.
n->Print();
}
|
 |