Big-O
Big-O notation is one of the ways in which we talk about how complex an algorithm or program is. It gives us a nice way of quantifying or classifying how fast or slow a program is as a function of the size of its input, and independently of the machine on which it runs.
Examples
Let's look at a program (in src/linear1.cpp):
/* This program takes a number n on standard input.
It then executes a for loop that iterates n times, counting the iterations.
It prints the number of iterations and a timing that uses the system call gettimeofday().
That's why you need to include <sys/time.h>. */
#include <sys/time.h>
#include <cstdio>
#include <iostream>
using namespace std;
int main()
{
long long n, count, i;
double start_time, end_time;
struct timeval tv;
if (!(cin >> n)) return 1;
/* Get the starting time. */
gettimeofday(&tv, NULL);
start_time = tv.tv_usec;
start_time /= 1000000.0;
start_time += tv.tv_sec;
/* Here's the loop, that executes n times. */
count = 0;
for (i = 0; i < n; i++) count++;
/* Get the ending time. */
gettimeofday(&tv, NULL);
end_time = tv.tv_usec;
end_time /= 1000000.0;
end_time += tv.tv_sec;
/* Print N, the iterations, and the time. */
printf("N: %lld Count: %lld Time: %.3lf\n", n, count, end_time - start_time);
return 0;
}
|
Obviously, this is a simple program. I don't want to go into gettimeofday too much. It returns the value of a timer, which includes seconds and microseconds. I convert that to a double, so that we can print out the timing the for loop. Suppose we run this program with varying values of n. What do we expect? Well, as n increases, so will the count, and so will the running time of the program:
(This is on my Macbook, chunking along at 2.2 Ghz in 2019):
UNIX> echo 100000 | bin/linear1 N: 100000 Count: 100000 Time: 0.000 UNIX> echo 1000000 | bin/linear1 N: 1000000 Count: 1000000 Time: 0.003 UNIX> echo 10000000 | bin/linear1 N: 10000000 Count: 10000000 Time: 0.020 UNIX> echo 100000000 | bin/linear1 N: 100000000 Count: 100000000 Time: 0.195 UNIX> echo 1000000000 | bin/linear1 N: 1000000000 Count: 1000000000 Time: 2.021 UNIX>Just what you'd think. The running time is roughly linear. Now, I'm also going to run this on a Raspberry Pi 3, which is a slower machine -- I'll tabulate the times below:
| n | Time on Macbook (s) | Time on Pi 3 (s) |
| 1,000,000 | 0.003 | 0.021 |
| 10,000,000 | 0.020 | 0.143 |
| 100,000,000 | 0.195 | 1.201 |
| 1,000,000,000 | 2.021 | 11.779 |
As you can see, the running time on both machines scales linearly with n. The Pi is slower, but the relative behavior of the two machines is the same.
Now, look at six other programs below. I will just show their loops:
src/linear2.cpp:/* This loop executes 2n times. */ count = 0; for (i = 0; i < 2*n; i++) count++; |
src/log.cpp:/* This loop executes log_2(n) times. */ count = 0; for (i = 1; i < n; i *= 2) count++; |
src/nlogn.cpp:
/* This loop executes n*log_2(n) times. */
count = 0;
for (j = 0; j < n; j++) {
for (i = 1; i < n; i *= 2) {
count++;
}
}
|
src/nsquared.cpp:
/* This loop executes n*n times. */
count = 0;
for (j = 0; j < n; j++) {
for (i = 0; i < n; i++) {
count++;
}
}
|
src/all_i_j_pairs.cpp:
/* This loop executes (n - 1) * n / 2 times.
It arises when you enumerate all (i,j) pairs
such as 0 <= i < j < n. */
count = 0;
for (j = 0; j < n; j++) {
for (i = 0; i < j; i++) {
count++;
}
}
|
src/two_to_the_n.cpp:
/* This loop executes 2^n times. */
count = 0;
for (i = 0; i < (1LL << n); i++) {
count++;
}
|
In each of the programs, I tell you how many times the loop executes in the comment. That will be the final value of count. Make sure you can calculate all of these below -- it's an easy test question:
UNIX> echo 16 | bin/linear1 N: 16 Count: 16 Time: 0.000 UNIX> echo 16 | bin/linear2 N: 16 Count: 32 Time: 0.000 UNIX> echo 16 | bin/log N: 16 Count: 4 Time: 0.000 UNIX> echo 16 | bin/nlogn N: 16 Count: 64 Time: 0.000 UNIX> echo 16 | bin/nsquared N: 16 Count: 256 Time: 0.000 UNIX> echo 16 | bin/all_i_j_pairs N: 16 Count: 120 Time: 0.000 UNIX> echo 16 | bin/two_to_the_n N: 16 Count: 65536 Time: 0.000 UNIX>In each program, the running time is going to be directly proportional to count. So, what do the running times look like if you increase n to large values? To test this, I ran all of the programs with increasing values of n. I quit either when n got really large (about 1015), or when the running time exceeded a minute. You can see the data in the following files (these are in the data directory):
| linear1 | linear2 | log | nlogn | nsquared | all_i_j_pairs | two_to_the_n |
log N: 7500000000000000 Count: 53 Time: 0.000 linear1 N: 50000000000 Count: 50000000000 Time: 98.628 linear2 N: 25000000000 Count: 50000000000 Time: 99.176 nlogn N: 2500000000 Count: 80000000000 Time: 167.156 nsquared N: 250000 Count: 62500000000 Time: 125.680 all_i_j_pairs N: 250000 Count: 31249875000 Time: 61.589 two_to_the_n N: 35 Count: 34359738368 Time: 76.261 |
Two quick observations: log(n) is really fast. On the flip side, 2n is really slow. Below I show some graphs of the data. The graphs all graph the same data; they just have different scales, so that you can do some visual comparisons:
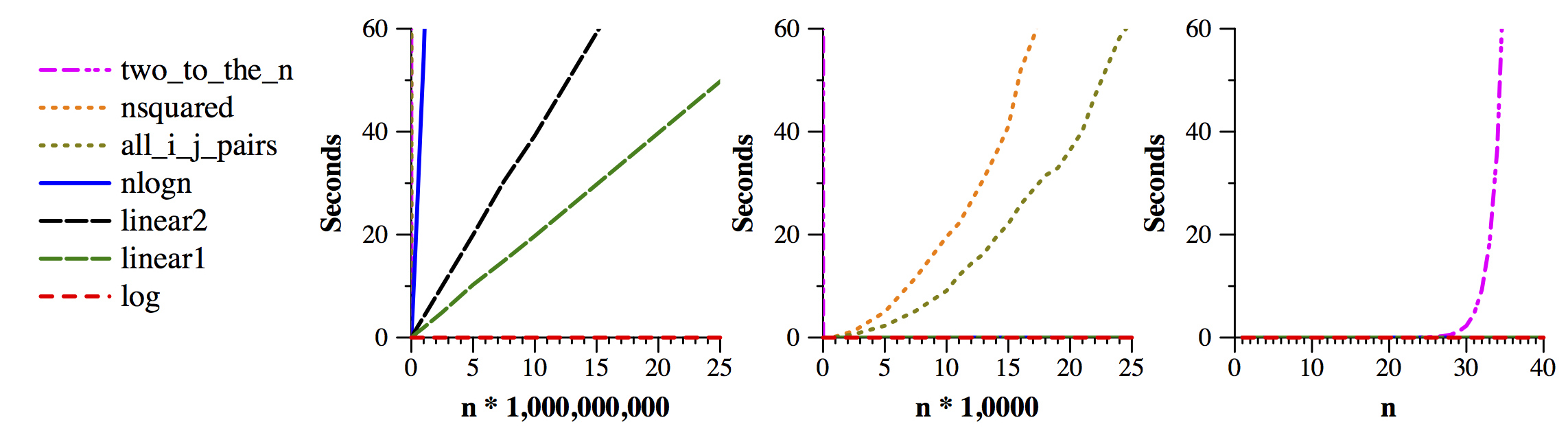 |
So, this shows what you'd think:
Back to Big-O: Function comparison
Big-O notation tries to work on classifying functions. The functions that we care about are the running times of programs. The first concept when we deal with Big-O is comparing functions. Basically, we will say that one function f(n)is greater than another g(n) if there is a value x0 so that for all x >= x0:Put graphically, it means that after a certain point on the x axis, as we go right, the curve for f(n) will always be higher than g(n). Thus, given the graphs above, you can see that n*n is greater than n*log(n), which is greater than 2n, which is greater than n, which is greater than log(n).
So, here are some functions:
- a(n) = 1
- b(n) = 100
- c(n) = 6-n
- d(n) = n
- e(n) = 2n
- f(n) = 2n-5
- g(n) = n*n - 5,000,000,000
- h(n) = log(n)
- i(n) = log(n) - 100
- j(n) = n*log(n)-100
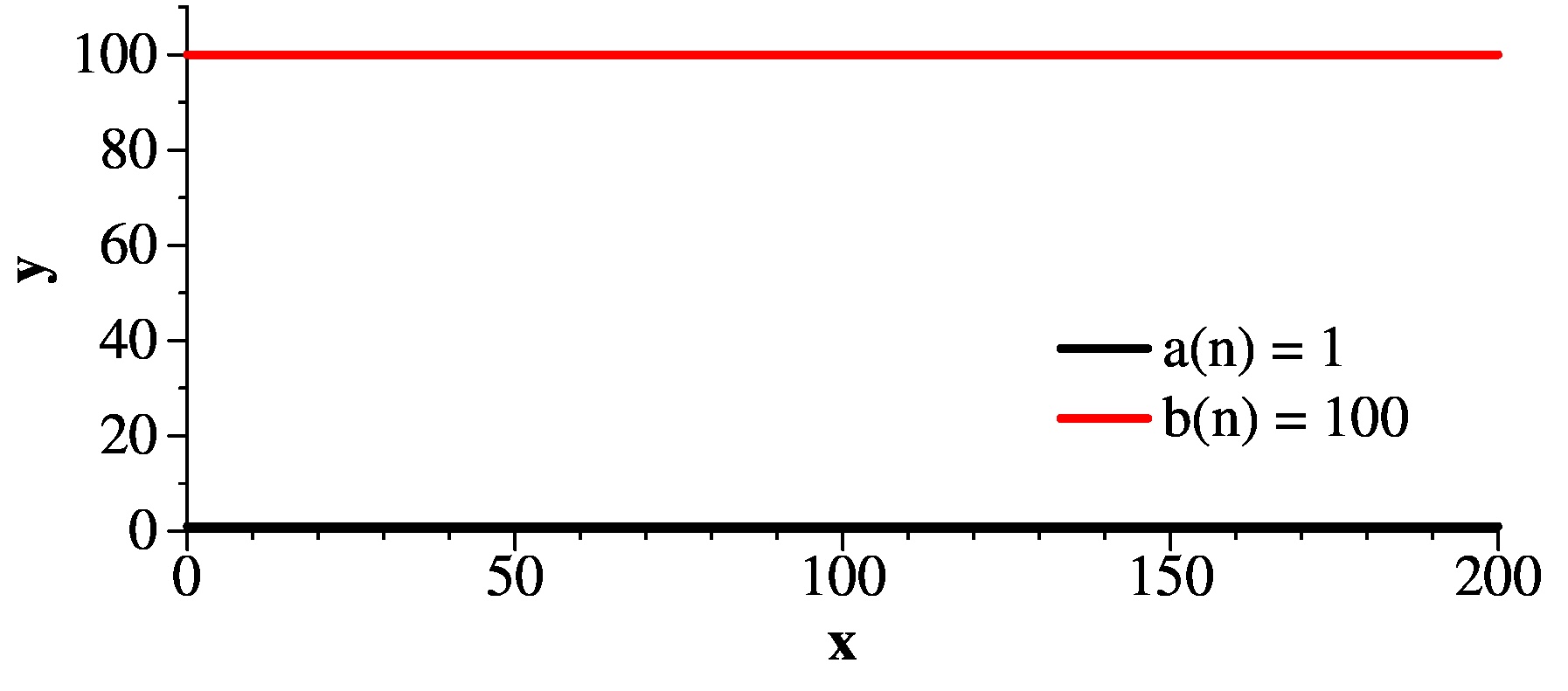 |
That was easy. How about d(n) and b(n)? d(n) is greater, and to demonstrate it, we need to pick a value of x0. We can't pick 0, because b(0) is 100 and d(0) is 0. However, if we pick x0 to be 101, now it works -- every value of d(n) is greater than 100 when n > 101.
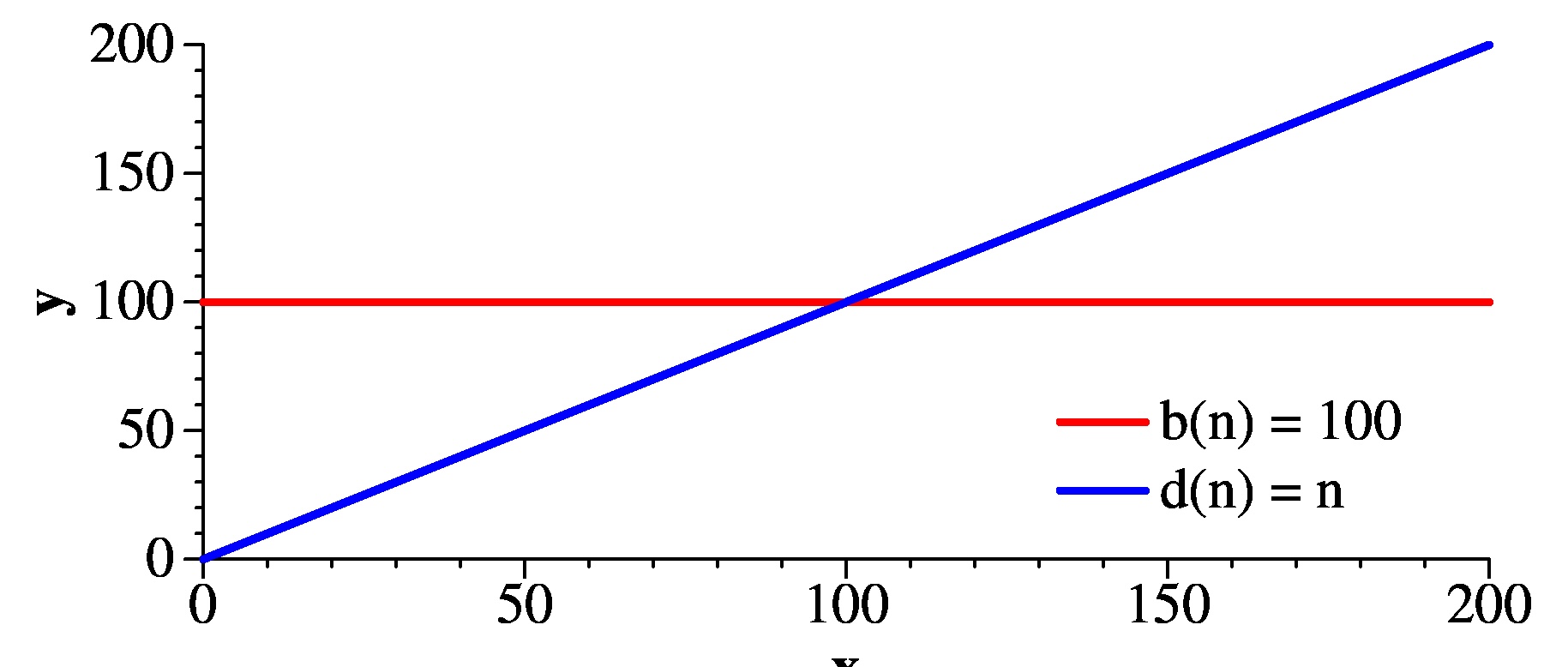 |
Similarly, look at d(n) and f(n). For small values of n, d(n) is greater. However, once x grows past 6, f(n) is greater:
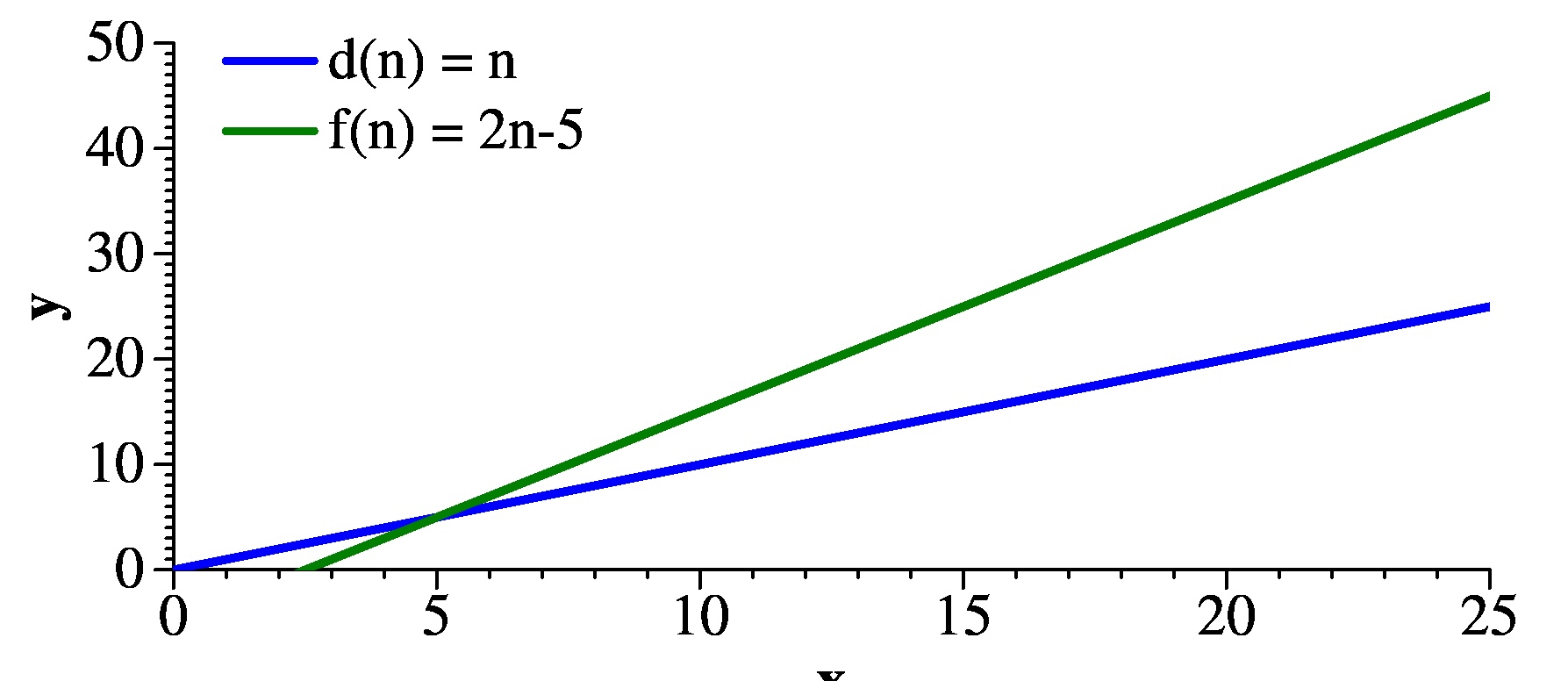 |
For a more drastic example, look at g(n) and d(n). For small values of n, d(n) is a lot greater. However, let's consider a large value of x0, like 100,000. d(n) = 100,000. And g(n) = 10,000,000,000 - 5,000,000,000, which is 5,000,000. That's much bigger than d(n). Plus, as n grows bigger than x0, g(n) grows more quickly than d(n). Therefore, g(n) > d(n).
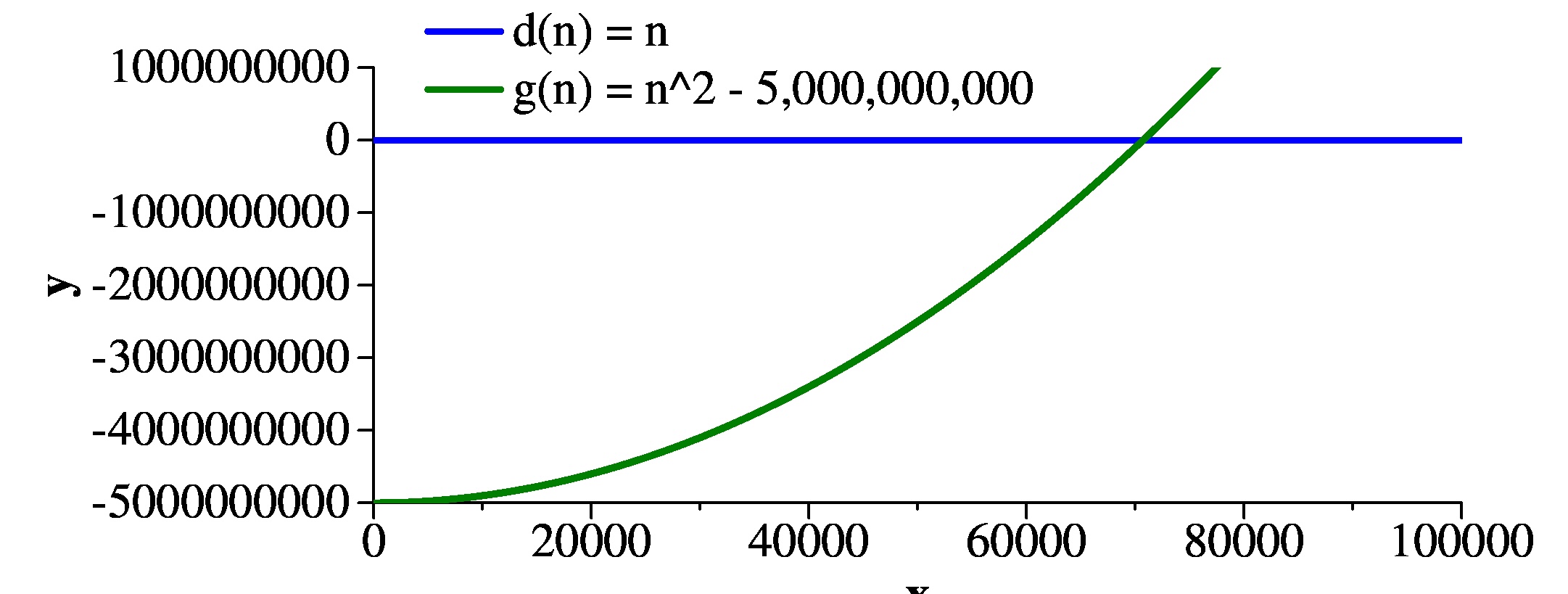 |
Here's a final example -- just look at the graph. y(n) is greater for x up to roughly 200. Then it dips down until x gets to roughly 475, at which point that x4 term takes over. After that, y(n) is greater than x(n), so y(n) is the greater function.
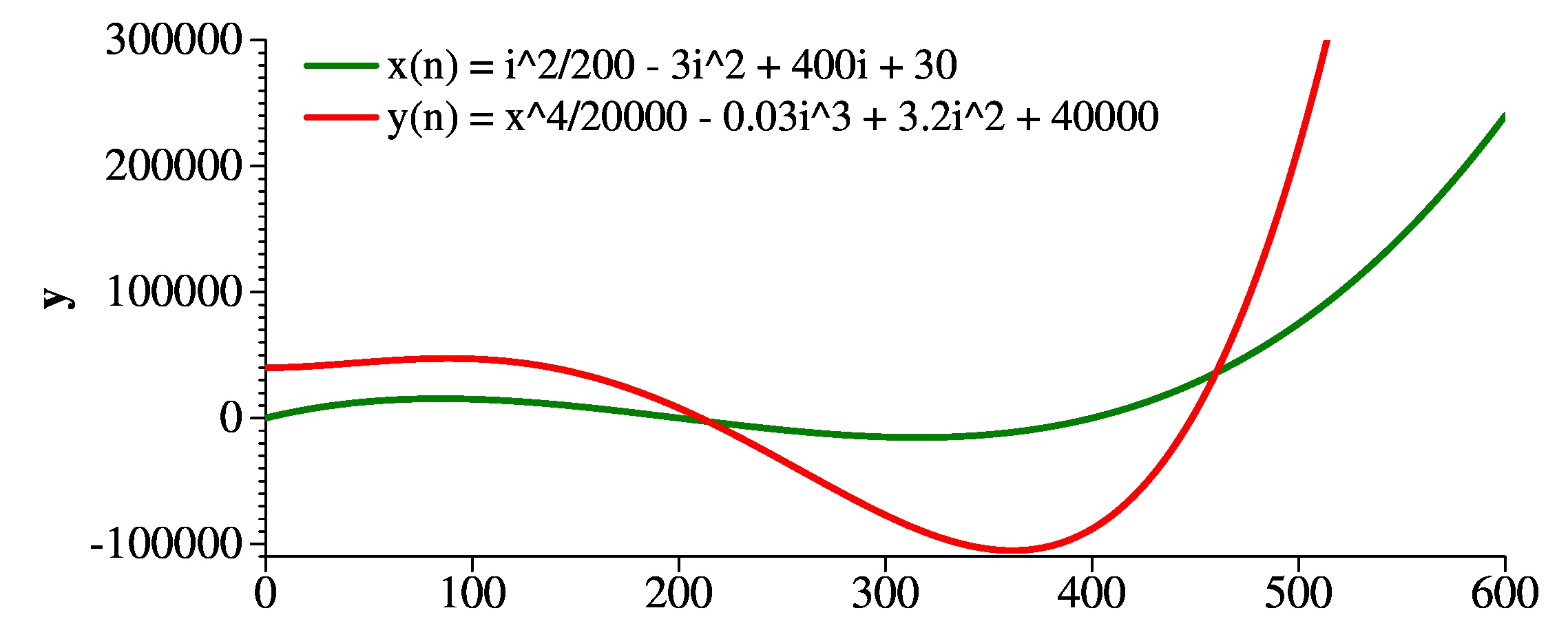 |
Here's a total ordering of the above functions. Make sure you can prove all of these to yourselves:
Some rules:
- If f(n) and g(n) are both polynomials of degree k, then the lead coefficient defines which one is greater.
- If f(n) is a polynomial of degree k and g(n) is a polynomial of degree l < k, and both lead coefficients are positive, then f(n) > g(n).
- If a*f(n) > b*g(n) for all positive constants a and b, then c*f(n) + d*g(n) > e*f(n) + x*g(n) if and only if c > e. For example, 20n*n - 100n > 19n*n + 60,000n.
Big-O
Given the above, we can now define Big-O:
Given the definitions of a(n) through j(n) above:
- a(n) = O(1).
- b(n) = O(1). This is because we can set c to 101. If that confuses you,
go back to the equation above: c*f(N) = 101(1) = 101. On the flip side, T(N) = 100.
Therefore for all N, c*F(N) ≥ T(N), because 101 > 101.
You should see that we can set c to any value ≥ 100. I chose 101, because it's the smallest value where c*F(N) > T(N), and I find "greater than" clearer than "greater than or equal to." That's just me.
- Let's ignore c(n). It's too weird.
- d(n) = O(n). Why? Set c equal to 2 and x0 equal to 1. It's pretty easy to see that 2N ≥ N for all N > 1.
- e(n) = O(n) too. Set c equal to 3 and x0 equal to 1. For all values of N ≥ 1, 3N is indeed greater than 2N.
- f(n) = O(n) too. Set c equal to 3 and
now, you can set x0 equal to -4 if you want. Why? Because 3*(-4) is -12,
which is greater than 2*(-4)-5 = -13. So, for all values of N ≥ -4, 3N ≥ 2N-5..
You don't have to set x0 to its smallest potential value. Any legal value can do, so in
this case you can set x0 to any value ≥ -4.
- g(n) = O(n2). Set c to 1 and x0 to anything.
- i(n) = O(log(n)). These are getting pretty obvious, no?
- j(n) = O(n*log(n)). Ditto.
The Imprecision of Big-O
O(f(N)) is an upper bound on T(N). That means that T(N) is definitely not bigger than f(n). We'd like it to be a tight bound, but often that is too difficult to prove. However, you should be aware of it. For example, although we showed above that b(n) = O(1), it is also true that b(n) = O(n2). Why? Well, set c equal to one, and x0 to 101, and you should see that for all values n ≥ 101, 1*n2 ≥ 100.So, in some respects, Big-O is imprecise, because b(n) above is not only O(1), but O(n), O(n2), O(n*log(n)), O(2n) and O(n!). In computer science, when we say that a = O(f(n)), what we really mean is that f(n) is the smallest known function for which a = O(f(n)).
As an aside, don't use the imprecision as a way to get around test questions. For example, if I ask for the Big-O complexity of sorting a vector with n elements, you shouldn't answer O(n10), because you know that it's technically correct, and n10 is probably bigger than any function that we teach in this class. You will not get credit for that answer, and I will cite this text when you argue with me about it...
Big Omega and Big Theta
Big Omega and Big Theta are two more definitions that help to clean up the above imprecision with Big-O.
- Big-Omega: T(N) = Ω(f(N)) if f(N) = O(T(N)). While Big-O says that
T(N) is no bigger than a factor times f(N), Big-Omega says that
T(N) is no smaller than a factor times f(N).
- Big-Theta: T(N) = Θ(f(N)) if T(N) = O(f(N)) and T(N) = Ω(f(N)). Big-Theta is the most precise of these specifications. It says that T(N) and f(N) are equivalent to constant factors of each other.
The program is Ω(n): choose c = 1 and x0=1 (in other words, for any x ≥ 1, 3x+5 > x). However, it is not Ω(n2), because there is no c such that c(3x+5) ≥ x2. It is, however, Ω(1): choose c = 1 and x0=1 -- it's pretty easy to see that 3x + 5 > 1.
Now, we can put this in terms of Big-Theta. The program is Θ(n), but not Θ(n2) or Θ(1).
It is unfortunate that we as computer scientists quantify algorithms using Big-O rather than Big-Theta, but it is a fact of life. You need to know these definitions, and remember that most of the time, when we say something is Big-O, in reality it is also Big-Theta, which is much more precise.
At this point, I think that giving the Wikipedia page on Big-O a scan is a good idea. This includes:
- The introduction.
- The first two equations in the Formal Definition.
- The Example.
- The Infinite asymptotics section.
- The Equals Sign section.
- The Orders of common functions section (ignore the "L-notation" line).
- The definitions of Big-O, Big-Omega and Big-Theta in the Family of Bachmann-Landau notations section.
- The text starting with "Aside from Big-O notation, ..." until the end of the section.
Using Big-O to Categorize
Although Big-O is laden with math, we use it to characterize the running times of programs and algorithms. The following Big-O characterizations are particularly useful (and they are all Big-Theta as well, even though we don't say so).- O(1): This is called "constant time." Any time a program takes a constant
number of instructions, regardless of the input, it is constant time. For example, arithmetic
is constant time. Moreover,
determining the size of a vector is O(1), regardless of the size of the vector,
because the STL stores the size as part of the vector.
Appending an element to a list, deque or vector is O(1). Pushing an element onto the front of a list or deque is O(1). Accessing any element of a vector or deque is also O(1).
Calling begin() or end() on any of the STL's data structures -- vector, deque, list, set or map -- is O(1). So is calling ++ or -- on an iterator. Perhaps you find that to be counterintuitive with a set or map, but so be it.
- O(n): This is called "linear." This is when the program takes time that is
directly proportional to size of its input. For example, creating a vector, list or
deque with n elements is O(n). Of course, creating the vector is faster,
but they are both linear, and their performance is directly proportional to n.
This is why we have the constant c in the definition of Big-O -- so that both
of these are O(n), even though the vector version is faster.
Traversing a set or map with an iterator is also O(n). This confuses students, because the other operations on sets or map involve logarithms. So, memorize it. Hopefully, when you learn about AVL trees, you'll get a better feeling for that.
And finally, deleting an element or inserting an element in the front of a vector is also O(n). This is why you don't want to use a vector for this operation.
- O(n2): This is called "quadratic time," and as the graphs above show,
it does not scale well. In particular, when n hits a value of 10,000, n2
gets pretty big (100,000,000). The all_i_j_pairs program above has count equal
(n+1)n/2. This is O(n2) as well.
- O(log(n)): This is called "log time." Now, you may ask "what base?" The
answer is that the base doesn't matter. Why is that? Because:
logb(c) = loga(c) / loga(b). Since loga(b) is a constant, for the purposes of Big-O, it doesn't matter. That may seem confusing, so make it concrete. If a = log10(n), then log2(n) = log2(10)*a. Since log2(10) is a constant (a little greater than three), for the purposes of Big-O, logarithms in base 10 and base 2 are equivalent.
Insertion, deletion, and finding elements in sets and maps with n elements are O(log(n)) operations. Binary search on a vector of n elements is also O(log(n)).
- O(n*log(n)): This is called "N log N." Creating maps and sets are
O(n*log(n)) operations. So is sorting a vector with n elements.
- O(2n): This is called "exponential" time. Exponential time is super-slow. This is the number of n digit binary numbers. It is also the number of subsets of a set with n elements (this is called the "power set". You don't have to worry about power sets until CS302).
Two Big-O Proofs
You are not responsible for proofs like this, but it's not a bad idea to see them:Is n*n + n + 1 = O(n*n)? See the following PDF file for a proof.
Generalizing, is an*n + bn + d = O(n*n) for a,b,d > 1 and b > d? See the following PDF file for a proof.