 |
Priority queues are very natual data structures for event-based simulation. In such a simulation, you define events that occur at given times. To run the simulation, you insert each event into a priority queue (keyed on time). Then you process the simulation by:
void PQ::Push(int v) { S.insert(v); }
int PQ::Pop(int v) { int rv; rv = *S.begin(); S.erase(S.begin()); return rv; }
size_t PQ::Size() { return S.size(); }
bool PQ::Empty() { return S.empty(); }
void PQ::Clear() { S.clear(); }
// The default constructor can be used for the parameterless constructor.
// The default destructor works, too.
// You'll also note that the default copy constructor & assignment overload also work.
PQ::PQ(const vector <int> &v) { size_t i; for (i = 0; i < v.size(); i++) S.insert(v[i]); }
|
Let's talk running times:
 |
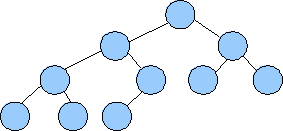
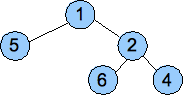
The other property of a heap is that the value of each node must be less than or equal to all of the values in its subtrees. That's it. Below are two examples of heaps:
 |
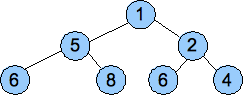 |
That second one has duplicate values (two sixes), but that's ok. It still fits the definition of a heap.
Below are three examples of non-heaps:
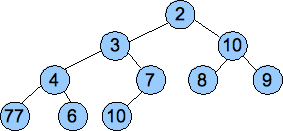 The 10 node is not smaller than the values in its subtrees. |
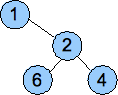 Not a complete tree. |
 The last row is not filled from left to right. |
When we push a value onto a heap, we know where the new node is going to go. So we insert the value there. Unfortunately, that may not result in a new heap, so we adjust the heap by "percolating up." To percolate up, we look at the value's parent. If the parent is smaller than the value, then we can quit -- we have a valid heap. Otherwise, we swap the value with its parent, and continue percolating up.
Below we give an example of inserting the value 2 into a heap:
| Start
|
Put 2 into the new node and percolate up.
|
| Continue percolating, since 2 is less than 3.
|
Now we stop, since 1 is less than 2.
|
To pop a value off a heap, again, we know the shape of the tree when we're done -- we will lose the rightmost node on the last level. So what we do is put the value in that node into the root (we will return the old value of the root as the return value of the Pop() call). Of course, we may not be left with a heap, so as in the previous example, we must modify the heap. We do that by "Percolating Down." This is a little more complex than percolating up. To percolate down, we check a value against its children. If it is the smallest of the three, then we're done. Otherwise, we swap it with the child that has the minimum value, and continue percolating down.
As before, an example helps. We will call Pop() on the last heap above. This will return 1 to the user, and will delete the node holding the 7, so we put the value 7 into the root and start percolating down:
| Start
|
Swap 7 and 2
|
| Swap 7 and 3. We're Done.
|
If we think about running time complexity, obviously the depth of a heap with n elements is log2(n). Thus, Push() and Pop() both run with O(log(n)) complexity. This is the exact same as using a multiset above. So why do we bother?
 |
 |
When we Push() an element onto the heap, we perform a push_back() on the vector, and then we percolate up. When we Pop() an element off the heap, we store the root, replace it with the last element, call pop_back() on the vector, and percolate down starting at the root. A quick inspection of the indices shows that:
/* This program implements Push() on a heap.
Its main reads a vector of integers on standard input, and then pushes them all onto
a heap, printing the heap each time. */
#include <vector>
#include <cstdio>
#include <cstdlib>
#include <iostream>
using namespace std;
/* Push the value val onto the heap. */
void Push(vector <int> &heap, int val)
{
int i, p;
i = heap.size();
heap.push_back(val); // Put the value onto the end of the heap.
while (i > 0) { // Percolate up, starting at i.
p = (i-1) / 2; // You stop when you reach the root, or when the parent's value
if (heap[p] > val) { // is less than or equal to val.
heap[i] = heap[p];
heap[p] = val;
i = p;
} else {
return;
}
}
}
int main()
{
vector <int> v;
vector <int> heap;
int val;
size_t i, j;
/* Read values into a vector */
while (cin >> val) v.push_back(val);
/* Repeatedly call Push and print the heap. */
for (i = 0; i < v.size(); i++) {
Push(heap, v[i]);
printf("Push %2d : ", v[i]);
for (j = 0; j < heap.size(); j++) printf(" %2d", heap[j]);
printf("\n");
}
return 0;
}
|
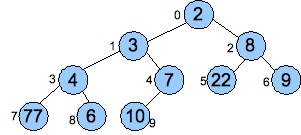
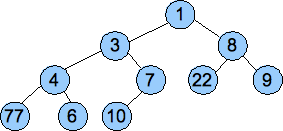
To illustrate the heap working, we'll insert numbers the numbers 7, 4, 22, 1, 7, 8, 9, 6, 3, 10 and 2:
UNIX> echo 7 4 22 1 7 8 9 6 3 10 2 | bin/push Push 7 : 7 Push 4 : 4 7 Push 22 : 4 7 22 Push 1 : 1 4 22 7 Push 7 : 1 4 22 7 7 Push 8 : 1 4 8 7 7 22 Push 9 : 1 4 8 7 7 22 9 Push 6 : 1 4 8 6 7 22 9 7 Push 3 : 1 3 8 4 7 22 9 7 6 Push 10 : 1 3 8 4 7 22 9 7 6 10 Push 2 : 1 2 8 4 3 22 9 7 6 10 7 UNIX>You should be able to see that the last two lines are the two heaps from our insertion example above:
 |  |
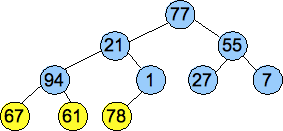
Below is an example. Here's the vector that we want to turn into a heap:
| 77 | 21 | 55 | 94 | 1 | 27 | 7 | 67 | 61 | 78 |
We convert the vector into a tree, as pictured below, and then we call Percolate_Down() on nodes of each successively higher level. These are the nodes pictured in yellow. By the time we get to the root, we have created a valid heap:
 |
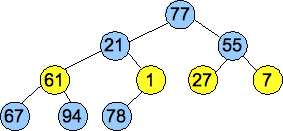 |
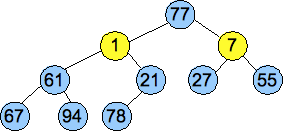 |
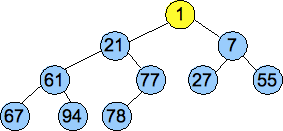 |
To analyze the running time complexity, we need a little math. Suppose our tree is complete at each level. The tree has n nodes, and thus its depth is log(n). The worst case performance of Percolate_Down() for a node at level i is log(n)-i. Thus, the performance of Percolate_Down() for a node at the bottom level is 1; for a node at the penultimate level, it is 2, etc.
The bottom level contains (n+1)/2 nodes, which is roughly n/2. Thus, all of the Percolate_Down()'s take (1)(n/2) = n/2 operations. At the next level, there are n/4 nodes, whose Percolate_Down()'s take 2 operations each. Thus, all of them take 2n/4. At the next level, there are n/8 nodes whose Percolate_Down()'s take 3 operations each. Thus, all of them take 3n/8. Do you see the pattern?
The creation of the heap can be converted into a summation:
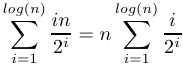 |
To figure out what that second summation is, let's first write a quick C++ program to calculate its value for the first 15 values of n. The code is below (src/formula.cpp), and to the right, we show its output:
#include <iostream>
using namespace std;
int main()
{
double num, den, total, n;
num = 1;
den = 2;
total = 0;
for (n = 0; n < 15; n++) {
total += (num/den);
num++;
den *= 2;
cout << total << endl;
}
}
| UNIX> bin/formula 0.5 1 1.375 1.625 1.78125 1.875 1.92969 1.96094 1.97852 1.98828 1.99365 1.99658 1.99817 1.99902 1.99948 UNIX> |
Looks like it converges to 2. Let's analyze it mathematically. Consider the following sum:
 |
Now, let's consider the equation G - G/2:
 |
From high school math, we know that this last summation equals one, so G - G/2 = 1, which means that G = 2.
 |
That graph sucks. I include it because I see students make graphs like these, and they need to have a more critical eye. Problem #1 is the squiggly lines -- what they indicate is that the individual data points have some variance, and that we should run more than one run per test, averaging the results. Still, if we ignore the squiggly lines, we draw two conclusions:
Instead, I wrote a second program that creates the random vector, calls the constructor and exits. I made it so that it could run for multiple iterations, so that if it was too fast, the multiple iterations allowed me to time it effectively.
 |
There -- that shows what we expect to see. It does make a difference!
I show this test to let you know that experimental computer science research can be very tricky. We had a simple goal: to demonstrate that a O(n) algorithm runs faster than a O(n(log(n))) one. We tried an obvious solution, and we couldn't use it because we weren't really testing what we wanted to test. When we rewrote our testing programs to do a better job of removing the noise from the experiment, we were able to demonstrate improved performance.