Experiment to show the effect of modifying the number of bins when inserting 10,000,000 random elements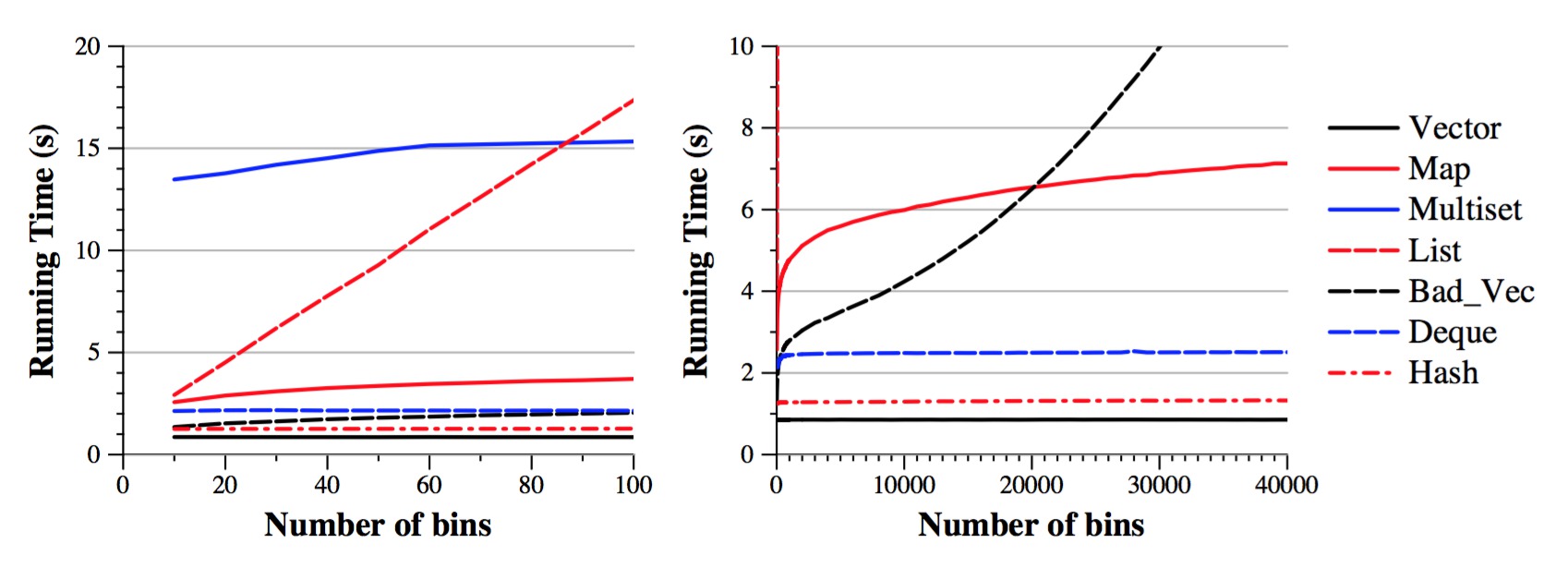 |
After that, I go through a bunch of Topcoder problems, discuss their solutions (without implementing them), and then discuss the running times of the solution.
The goal of this set of lecture notes is to help you be able to take a problem and its solution, and derive the running time of the solution in terms of big-O.
I have implemented the class seven different ways, in seven different class implementations. They all work, but they all work differently. They provide an excellent review of the data structures that we've learned in this class. They are:
Because I know this will be confusing to some, let me simple show Minimum_Value and Elts after a few Add_Value() calls. We'll assume that the bin size is 10:
Action Minimum_Value Elts
----------- ------------- ----
Start: -1 {}
Add_Value(55) 5 { 1 } # We resize the deque by 1
Add_Value(71) 5 { 1, 0, 1 } # We resize the deque by 2
Add_Value(58) 5 { 2, 0, 1 }
Add_Value(15) 1 { 1, 0, 0, 0, 2, 0, 1 } # We insert four 0's to the front of the deque.
Add_Value(26) 1 { 1, 1, 0, 0, 2, 0, 1 }
I'm not going to go through any of the code -- it's pretty straightforward, and it is commented. You'll note that all of the implementations use the (void *) as detailed in the (void *) lecture.
| Vector | Map | Unordered_map | Multiset | List | Bad_Vec | Deque | |
| Create | O(n + max) | O(n log(bins)) | O(n) | O(n log(n)) | O(n * bins) | O(n log(bins) + bins2) | O(n + (max-min)) |
| Get_Data | O(max) | O(bins) | O(bins log(bins)) | O(n) | O(bins) | O(bins) | O(max-min) |
| Space | O(max) | O(bins) | O(bins) | O(n) | O(bins) | O(bins) | O(max-min) |
Get_Data: The vector has max elements, so traversing it is O(max). The size of the two resulting vectors will be bins, but clearly bins ≤ max. That is why it is O(max).
Space: The space is the size of the vector, which is max elements.
You may wonder -- shouldn't it be O(n log(bins) + bins log(bins))? That would account for the n find operations and the bins insertions. The answer is no. Why? because bins is clearly less than or equal to n. So (bins log(bins)) is less than or equal to (n log(bins)). Remember from our discourse on Big-O that constant factors don't matter with Big-O:
Get_Data: The map has bins elements, so traversing it is O(bins).
Space: The space is the size of the map, which is bins elements. Maps are implemented as balanced binary trees, and a tree with bins nodes consumes O(bins) space. Now, the map with bins elements is a lot bigger than a vector with bins elements, because the vector is very space efficient. However, they are both O(bins), because constant factors don't matter with Big-O.
Get_Data: The unordered_map has bins elements, so traversing it to create bin_ids is O(bins). Sorting bin_ids is O(bins log(bins)). Then, each find() is O(1), so creating num_elts is O(bins). The total running time is therefore O(bins log(bins)).
Space: The space is the size of the unordered_map, which is O(bins).
You may wonder -- when we're filling up the multiset, it has fewer than n elements, so why not something smaller than O(n log(n))? It's a good question, so let me prove to you that it is indeed O(n log(n)). Let's just consider the second half of the insertions. There are n/2 of these, and the multset contains at least n/2 elements in each insertion. So, the performance of those n/2 insertions is at least as big as O(n/2 log(n/2)). The constant factor doesn't matter, so this is O(n log(n/2)). And what is log(n/2)? It is log(n)-1. We know that O(x-1) is O(x), so O(log(n/2)) is O(log(n)). Therefore, the last n/2 insertions are O(n log(n)). The first n/2 insertions will be quicker than the second n/2, so they are less than O(n log(n)). So the n insertions are indeed O(n log(n)).
Get_Data: The multiset has n elements, so traversing it is O(n).
Space: The space is the size of the multiset, which is n elements.
Get_Data: The list has bins elements, so traversing it is O(bins).
Space: The space is the size of the list, which has bins elements.
Get_Data: The vectors have bins elements, so copying them is O(bins).
Space: The space is the size of the vectors, which is bins elements each. O(2*bins) is, of course, O(bins).
Get_Data: The deque has (max-min) elements, so traversing it is O(max-min).
Space: The space is the size of the deque.
UNIX> time sh -c "echo 0 100000000 | bin/dth_vector 1" # Vector = 1 second
0 1
1e+08 1
1.008u 0.114s 0:01.12 99.1% 0+0k 0+0io 0pf+0w
UNIX> time sh -c "echo 0 100000000 | bin/dth_map 1" # Map = negligible
0 1
1e+08 1
0.002u 0.003s 0:00.00 0.0% 0+0k 0+0io 0pf+0w
UNIX> time sh -c "echo 0 100000000 | bin/dth_unordered_map 1" # Unordered_map = negligible
0 1
1e+08 1
0.004u 0.005s 0:00.01 100.0% 0+0k 0+0io 0pf+0w
UNIX> time sh -c "echo 0 100000000 | bin/dth_multiset 1" # Multiset = negligible
0 1
1e+08 1
0.002u 0.004s 0:00.01 0.0% 0+0k 0+0io 10pf+0w
UNIX> time sh -c "echo 0 100000000 | bin/dth_list 1" # List = negligible
0 1
1e+08 1
0.002u 0.003s 0:00.00 0.0% 0+0k 0+0io 0pf+0w
UNIX> time sh -c "echo 0 100000000 | bin/dth_bad_vec 1" # Bad_Vec = negligible
0 1
1e+08 1
0.002u 0.003s 0:00.00 0.0% 0+0k 0+0io 0pf+0w
UNIX> time sh -c "echo 0 100000000 | bin/dth_deque 1" # Deque = 2 seconds
0 1
1e+08 1
2.009u 0.147s 0:02.16 99.0% 0+0k 0+0io 0pf+0w
UNIX>
Let's use src/range_tester.cpp to test some other scenarios. Let's remind ourselves
how it works:
UNIX> bin/range_vector usage: range_tester bin_size n low high seed print(Y|N) UNIX>How about this: Let's insert 10,000,000 data points and modify the maximum values of the data points so that we modify the number of bins. You can see below that if we specify high as one, we get one bin, and if we specify high as 100,000, we get 100,000 bins:
UNIX> bin/range_vector 1 10000000 0 1 5 Y # Here there's just one bin.
0 10000000
Time for Create: 0.234
Time for Get_Data: 0.000
UNIX> bin/range_vector 1 10000000 0 100000 5 Y | wc # Here there are 100,000 bins.
100002 200008 1800054 # (There are two lines for the timings)
UNIX> bin/range_vector 1 10000000 0 100000 5 N # The O(n) part of Create dominates.
Time for Create: 0.276
Time for Get_Data: 0.005
UNIX>
Let's run an experiment. For each of the implementations, I vary the number of
bins, and plot the time to add 10,000,000 values. I run over ten tests for each data
point, and average the results. This is on a mid-grade Linux box.
Experiment to show the effect of modifying the number of bins when inserting 10,000,000 random elements |
Let's see how this jibes with our understanding of the running times:
We can also conclude that vectors are more efficient data structures than deques. Let me quote from https://en.cppreference.com/w/cpp/container/deque:
| "As opposed to std::vector, the elements of a deque are not stored contiguously: typical implementations use a sequence of individually allocated fixed-size arrays, with additional bookkeeping, which means indexed access to deque must perform two pointer dereferences, compared to vector's indexed access which performs only one." |
The hash implementation is indeed fast, but it still performs more work than the vector implementation. It is slower by a factor of roughly 1.7. I surmised that compiler optimization might shrink that gap, but when I compiled both vector and hash with compiler optimization, it sped both of them up by more than a factor of two; however, the hash implementation was still 1.7 times slower.
What do you think of the shape of the map curve? Does it look like n log(bins) to you? Well, remember that we're holding n constant, so we should expect the curve to look like log (bins), and indeed it does. I like it when things make sense.
Let's look at two sets of timings:
Implementation: bins=10 bins=40,000 --------------- ------- ----------- vector 0.86 s 0.85 s map 2.57 s 7.12 s ratio map/vector 2.99 8.38 |
The log of 10 is 3.32 and the log of 40,000 is 15.28. So, the table above shows us that the map implementation is proportionally worse than the vector implementation when the number of bins is small (otherwise, we'd expect the ratio when bins equals 40,000 to be 15). Can we make sense of that? Yes -- what I surmise is that when you are calling find() on the map, its performance is (x + log(bins)), where x is some startup costs (maybe a few "if" statements). When bins is small, the x term is significant. As bins grows, it becomes less significant.
The list implementation's curve looks like a straight line, which also matches expectations. It's Big-O equation is O(n * bins), and we're holding n constant, so we should expect a straight line!
The "bad" vector implementation has a Big-O of O(n log(bins) + bins2). So, when we hold n constant, we expect the quadratic term to dominate, and indeed that curve looks quadratic.
Question: Why is the bad_vec curve better than the list's curve, when O(n*bins) is faster than O(bins2)? (remember, we're holding n constant? Because the list implementation is performing O(bins) for every Add_Value() call, due to its linear lookup of the value. The bad_vec implementation performs O(log(bins)) for every Add_Value() call, because it uses binary search to find the value, and only does an O(bins) operation when it has to insert a new value. When bins is 40,000, the ratio of insertions to finds is 40,000/10,000,000, or 0.004. This is why the bad_vec implementation is faster than the list implementation -- it does the slow operation very infrequently, while the list operation does it at every Add_Value() call.
Question: If we keep increasing the number of bins, will the bad_vector implementation eventually become slower than the list implementation? Well, the gap will keep closing, but in reality, the bad_vec implementation never becomes slower (try the shell script in scripts/list_vec.sh). This is because we can't have more than n bins, so we can't keep increasing the bin size until the O(bins2) term becomes bigger than O(n*bins).