One great use of recursion is to solve problems using exhaustive search with backtracking. What makes recursion nice is how easy it is to write the program. The basic structure is as follows:
You have a problem that you want to solve by assigning values to data. The values will have some interrelated constraints. You attempt to solve it by assigning all possible values to the first piece of data. When you assign a value, you make a recursive call to solve the rest of the problem. If successful, you're done. However, if solving the rest of the problem is unsuccessful, then you'll be alerted to this fact when the recursive call returns. You then remove the value that you have assigned, and assign the next value.
(BTW, the general technique in play here is Dynamic Programming, which we'll explore in detail in CS302. It improves upon the technique employed here, by utilizing a cache to store duplicate recursive calls. The lecture notes are in http://web.eecs.utk.edu/~jplank/plank/classes/cs302/Notes/DynamicProgramming/).
The example problem that we'll work on is Sudoku. A Sudoku puzzle is a 9x9 grid of numbers between 1 and 9. You are given a grid that is partially filled in, and your job is to fill the rest of the grid in so that:
- No row contains the same number twice.
- No column contains the same number twice.
- There are 9 3x3 panels in the grid, starting with the upper left-hand corner. No 3x3 panel may contain the same number twice.
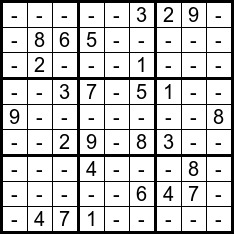 Example Problem |  Example Solution |
Program structure
To solve this problem, we'll define a Sudoku class, which has a familiar structure. It is in include/sudoku.hpp:
/* This class lets you store, print and solve Sudoku problems. */
#include <vector>
class Sudoku {
// There is no need for a constructor, destructor, copy constructor or assignment overload.
public:
void Clear(); // Clear the current puzzle
std::string Read_From_Stdin(); // Read a puzzle from standard input. Return "" on
// success, "EOF" on EOF, or an error string on failure.
void Print_Screen() const; // Print the puzzle to the screen
void Print_Magick() const; // Print commands for magick to make Sudoku.jpg
bool Solve(); // Solve the puzzle - returns false if unsolvable
// These are helper methods for both reading in the puzzle, and solving the puzzle,
// plus a vector of strings to store the puzzle.
protected:
bool Is_Row_Valid(int r) const;
bool Is_Col_Valid(int c) const;
bool Is_Panel_Valid(int sr, int sc) const;
bool Recursive_Solve(int r, int c);
std::vector <std::string> Grid;
};
|
The public methods are described in the header comments. My personal opinion is that the protected definitions shouldn't even be in the header, but they have to be, so they are. However, I don't feel the need to document them. My documentation is here:
- Is_Row_Valid() returns whether the given row is legal.
- Is_Col_Valid() returns whether the given column is legal.
- Is_Panel_Valid() returns whether the given 3x3 panel is legal. It takes the starting row and starting column of the panel.
- Recursive_Solve() is the recursive part of the solver. It takes a row r and a column c, and assumes that all cells before r and c have been filled in. It will find the next empty cell and try to solve the puzzle by filling in all possible entries for that cell, and then calling Recursive_Solve() recursively.
The comments state that there is no nead for a constructor, destructor, copy constructor or assignment overload. That means that an "empty" puzzle can exist, and will be a cleared Grid vector. Since vectors and strings destroy themselves, you don't need to probe any further to understand that you don't need a destructor. You'll need to understand the code to reason about the copy constructor and assignment overload, but it is straightforward -- the only state of the data structure is the Grid, and there are no pointers in the grid. So, if you copy the grid, you have copied the puzzle. The defaults work fine.
Sudoku_main.cpp
The file src/sudoku_main.cpp defines a main() routine that uses the Sudoku class. It is straightforward -- you call the program with two command line arguments. The first is "yes" or "no", specifying whether you want to solve the problem or just print it out. The second is "screen" or "magick", specifying the output format. You put the puzzles on standard input. This is straightforward code:
/* This is a main() routine that lets you solve sudoku puzzles on standard input.
It will read puzzles on standard input, and then let you:
- Either solve the puzzles or not.
- Print the puzzle (solved or not).
- You can print on the screen, or
- You can print commands for the magick program to make Sudoku.jpg
*/
#include <iostream>
#include <cstdlib>
#include "sudoku.hpp"
using namespace std;
/* Sometimes it's convenient to have a helper procedure to handle errors
on the command line. We could, of course, have used try/catch, but
the usage() command makes for cleaner code, in my opinion. */
void usage(const string &s)
{
cerr << "usage: sudoku solve(yes|no) output-type(screen|magick) - puzzles on stdin\n";
if (s != "") cerr << s << endl;
exit(1);
}
int main(int argc, char **argv)
{
string solve; // The first command line argument -- yes or no for whether to solve.
string output; // The second command line argument - "screen" or "magick"
Sudoku sud; // The puzzle.
string r; // The return value from Read_From_Stdin().
/* Parse the command line. */
if (argc != 3) usage("");
solve = argv[1];
output = argv[2];
if (solve != "yes" && solve != "no") usage("bad solve");
if (output != "screen" && output != "magick") usage("bad output");
if (output == "screen") cout << "-------------------" << endl;
while (1) {
/* Read the puzzle and handle EOF/errors */
r = sud.Read_From_Stdin();
if (r != "") {
if (r == "EOF") return 0;
cout << r << endl;
return 1;
}
/* Solve the puzzle if desired. **/
if (solve == "yes") {
if (!sud.Solve()) {
printf("Cannot solve puzzle\n");
}
}
/* Print the puzzle. */
if (output == "screen") {
sud.Print_Screen();
cout << "-------------------" << endl;
} else {
sud.Print_Magick();
}
/* Clear the puzzle and try again. (Clearing is unnecessary, but may as well test it.) */
sud.Clear();
}
}
|
Building a solution: Sudoku1.cpp
As always, it's best to build a solution incrementally, testing along the way. I have a makefile which helps you do compilation. I'll use it in my examples.We start with src/sudoku1.cpp, which simply defines dummy implementations for all the methods. It compiles, but doesn't do anything:
UNIX> make clean rm -f obj/* bin/* UNIX> make bin/sudoku1 g++ -std=c++98 -Wall -Wextra -Iinclude -c -o obj/sudoku1.o src/sudoku1.cpp g++ -std=c++98 -Wall -Wextra -Iinclude -c -o obj/sudoku_main.o src/sudoku_main.cpp g++ -std=c++98 -Wall -Wextra -Iinclude -o bin/sudoku1 obj/sudoku1.o obj/sudoku_main.o UNIX> bin/sudoku1 usage: sudoku solve(yes|no) output-type(screen|magick) - puzzles on stdin UNIX> bin/sudoku1 no screen Read_From_Stdin is not implemented yet UNIX>
Reading input: Sudoku2.cpp
Our next program, sudoku2.cpp, implements Read_From_Stdin() and Print_Screen(). Read_From_Stdin() reads the grid from standard input, doing a little error checking along the way. It simply reads characters, not caring about line or file formatting. Print_Screen() is also straightforward. (BTW, I implement Clear() here, too, but don't show it):
string Sudoku::Read_From_Stdin()
{
int i, j;
char c;
ostringstream oss; // This is to build an error string.
/* Read 81 characters, error checking for legal characters, and EOF.
The try/catch is nice because you want to clear the grid on all errors. */
Grid.clear();
Grid.resize(9);
try {
for (i = 0; i < 9; i++) {
for (j = 0; j < 9; j++) {
/* Handle EOF -- if nothing was read, return "EOF"; otherwise return an error. */
if (!(cin >> c)) {
if (i == 0 && j == 0 && cin.eof()) throw((string) "EOF");
throw((string) "Bad Sudoku File -- not enough entries");
}
/* Error check the digit. */
if (c == '-' || (c >= '0' && c <= '9')) {
Grid[i].push_back(c);
} else {
oss << "Bad character at row " << i << ", column " << j << ": " << c ;
throw(oss.str());
}
}
}
/* Clear the grid when you get an error. */
} catch (const string s) {
Grid.clear();
return s;
}
/* Otherwise, return "" on success. */
return "";
}
/* Print_Screen() prints the grid, putting a space between characters, an extra
space between panel columns, and an extra line between panel rows. */
void Sudoku::Print_Screen() const
{
size_t i, j;
for (i = 0; i < Grid.size(); i++) {
for (j = 0; j < Grid[i].size(); j++) {
if (j != 0) cout << " ";
cout << Grid[i][j];
if (j == 2 || j == 5) cout << " ";
}
cout << endl;
if (i == 2 || i == 5) cout << endl;
}
}
|
I have three example puzzles in txt/example1.txt, txt/example2.txt and txt/example3.txt. The last one is the one pictured above.
I also have some bad input files:
- txt/bad1.txt has a bad character in it.
- txt/bad2.txt has a row with duplicate entries.
- txt/bad3.txt has a column with duplicate entries.
- txt/bad4.txt has a panel with duplicate entries.
UNIX> make bin/sudoku2 g++ -std=c++98 -Wall -Wextra -Iinclude -c -o obj/sudoku2.o src/sudoku2.cpp g++ -std=c++98 -Wall -Wextra -Iinclude -c -o obj/sudoku_main.o src/sudoku_main.cpp g++ -std=c++98 -Wall -Wextra -Iinclude -o bin/sudoku2 obj/sudoku2.o obj/sudoku_main.o UNIX> cat txt/example1.txt txt/example2.txt | bin/sudoku2 no screen ------------------- - 6 - 1 - 4 - 5 - - - 8 3 - 5 6 - - 2 - - - - - - - 1 8 - - 4 - 7 - - 6 - - 6 - - - 3 - - 7 - - 9 - 1 - - 4 5 - - - - - - - 2 - - 7 2 - 6 9 - - - 4 - 5 - 8 - 7 - ------------------- 4 - 6 7 - - - - 9 - 2 5 - - - - 7 - - - - 5 9 - - 3 4 - - - - - - 3 - 2 - - 2 - 4 - 1 - - 7 - 1 - - - - - - 6 1 - - 3 2 - - - - 8 - - - - 4 2 - 2 - - - - 5 8 - 1 ------------------- UNIX> bin/sudoku2 no screen < txt/bad1.txt ------------------- Bad character at row 0, column 1: x UNIX> bin/sudoku2 no screen < txt/bad2.txt | sed -n 8p # I know that the bad row will be printed on line 8 7 - - 9 - 1 - - 7 UNIX>
Sudoku3 - Checking the input
In src/sudoku3.cpp, we write Is_Row_Valid() and Is_Col_Valid() to test whether rows and columns are valid. Go ahead and read the comment to see how Is_Row_Valid() works:
/* I use a boolean vector called check to check for row validity. For each digit i,
check[i] is false if I haven't seen the digit, and true if I have. That way,
I can identify when I have seen a digit twice. */
bool Sudoku::Is_Row_Valid(int r) const
{
size_t i;
vector <bool> check;
char c;
check.resize(9, false);
for (i = 0; i < 9; i++) {
c = Grid[r][i];
if (c != '-') {
c -= '1';
if (check[c]) return false;
check[c] = true;
}
}
return true;
}
|
I don't show Is_Col_Valid(), because it works in the exact same way. I also put code into Read_From_Stdin() to test that every row and column is valid. We can now identify that txt/bad2.txt and txt/bad3.txt are indeed bad:
UNIX> make bin/sudoku3 g++ -std=c++98 -Wall -Wextra -Iinclude -c -o obj/sudoku3.o src/sudoku3.cpp g++ -std=c++98 -Wall -Wextra -Iinclude -c -o obj/sudoku_main.o src/sudoku_main.cpp g++ -std=c++98 -Wall -Wextra -Iinclude -o bin/sudoku3 obj/sudoku3.o obj/sudoku_main.o UNIX> bin/sudoku3 no screen < txt/bad2.txt ------------------- Duplicate entry in row 5 UNIX> bin/sudoku3 no screen < txt/bad3.txt ------------------- Duplicate entry in column 6 UNIX>
Sudoku4 - Checking the input further
src/sudoku4.cpp implements Is_Panel_Valid(). This is similar enough to Is_Row_Valid() to need no further comment:
bool Sudoku::Is_Panel_Valid(int sr, int sc) const
{
int r;
int c;
vector <bool> check;
char ch;
check.resize(9, false);
for (r = sr; r < sr+3; r++) {
for (c = sc; c < sc+3; c++) {
ch = Grid[r][c];
if (ch != '-') {
ch -= '1';
if (check[ch]) return false;
check[ch] = true;
}
}
}
return true;
}
|
Now we can identify that txt/bad4.txt is bad:
UNIX> ma make bin/sudoku4 g++ -std=c++98 -Wall -Wextra -Iinclude -c -o obj/sudoku4.o src/sudoku4.cpp g++ -std=c++98 -Wall -Wextra -Iinclude -o bin/sudoku4 obj/sudoku4.o obj/sudoku_main.o UNIX> bin/sudoku4 no screen < txt/bad4.txt ------------------- Duplicate entry in panel starting at row 6 and column 6 UNIX>
Sudoku5 - Solving the puzzle
Now that we have our methods and error-checking in place, writing the solver (src/sudoku5.cpp) is relatively straightforward. The Solve() method simply calls Recursive_Solve(0, 0):
int Sudoku::Solve()
{
return Recursive_Solve(0, 0);
}
|
We will go over each part of Recursive_Solve() separately. The first part of it checks successive elements of the grid until it gets to the end of the grid, or it gets to a dash character. If it reaches the end of the grid, then the puzzle is solved, and it returns true.
int Sudoku::Recursive_Solve(int r, int c)
{
int i;
if (Grid.size() == 0) return false; // If there's no puzzle, return false.
/* Skip all non-dash characters */
while (r < 9 && Grid[r][c] != '-') {
c++;
if (c == 9) {
r++;
c = 0;
}
}
/* Base case -- we're done. Return success! */
if (r == 9) return true;
|
Next comes the recursive part. Once we've found a dash, we try to insert each value from '1' to '9'. When we insert a value, we test to see if the value's row, column and panel are valid. If so, then we call the solver recursively. We do that on r and c, because the recursive solver will skip over that element, now that it is no longer a dash. If the recursive solver returns true, then we have found a solution, and we return one:
/* Try each value. If successful, then return true. */
for (i = '1'; i <= '9'; i++) {
Grid[r][c] = i;
if (Is_Row_Valid(r) &&
Is_Col_Valid(c) &&
Is_Panel_Valid(r-r%3, c-c%3) &&
Recursive_Solve(r, c)) {
return true;
}
}
|
If we fall out of the for loop, that means that there was no solution. Therefore, we reset the element to a dash, and return 0. That way, the calling function can try another value and continue. If r and c are zero, the calling function is Solve(), and it will return that there is no solution to the puzzle:
/* If unsuccessful, reset the element and return false. */ Grid[r][c] = '-'; return false; } |
See how recursion makes this complex process of trying and backtracking so simple? There is no explicit backtracking really -- the important part is that if the recursive solver fails, it restores the state of the grid to the state when it was called, so that the caller can try something new.
When we run this, it solves the puzzles:
UNIX> cat txt/example*.txt | bin/sudoku5 yes screen ------------------- 9 6 3 1 7 4 2 5 8 1 7 8 3 2 5 6 4 9 2 5 4 6 8 9 7 3 1 8 2 1 4 3 7 5 9 6 4 9 6 8 5 2 3 1 7 7 3 5 9 6 1 8 2 4 5 8 9 7 1 3 4 6 2 3 1 7 2 4 6 9 8 5 6 4 2 5 9 8 1 7 3 ------------------- 4 3 6 7 2 8 5 1 9 9 2 5 3 1 4 6 7 8 1 7 8 5 9 6 2 3 4 8 6 9 1 5 7 3 4 2 3 5 2 6 4 9 1 8 7 7 4 1 2 8 3 9 5 6 6 1 4 8 3 2 7 9 5 5 8 7 9 6 1 4 2 3 2 9 3 4 7 5 8 6 1 ------------------- 1 3 7 8 9 4 6 5 2 5 8 2 6 7 1 3 9 4 4 6 9 3 5 2 1 8 7 8 5 6 7 3 9 4 2 1 7 9 4 2 1 6 5 3 8 3 2 1 5 4 8 7 6 9 2 7 8 1 6 3 9 4 5 9 1 3 4 2 5 8 7 6 6 4 5 9 8 7 2 1 3 ------------------- UNIX>It's pretty quick too. It may be disappointing to you that a program so simple can solve Sudoku problems so quickly. If you really wanted it to be fast, or if you wanted to solve larger puzzles, you would probably have to put some more smarts into the program. However, for puzzles of this size, the simple recursive solution works very well.
Sudoku.cpp - The final version
The final version of the program is in src/sudoku.cpp. It implements Print_Matick(), which puts the output into a format that the magick program (google Imagemagick) can understand. When you pipe it to the shell, it creates the file Sudoku.jpg, which is a picture of the puzzle. That's how I made jpg/example3-problem.jpg and jpg/example3-solution.jpg, which are pictured above:UNIX> make bin/sudoku g++ -std=c++98 -Wall -Wextra -Iinclude -c -o obj/sudoku.o src/sudoku.cpp g++ -std=c++98 -Wall -Wextra -Iinclude -c -o obj/sudoku_main.o src/sudoku_main.cpp g++ -std=c++98 -Wall -Wextra -Iinclude -o bin/sudoku obj/sudoku.o obj/sudoku_main.o UNIX> bin/sudoku no magick < txt/example3.txt | head magick -size 234x234 xc:Black \ -background White -fill Black \ \( -size 24x24 -gravity Center label:- \) -geometry 24x24+3+3 -gravity NorthWest -composite \ \( -size 24x24 -gravity Center label:- \) -geometry 24x24+3+28 -gravity NorthWest -composite \ \( -size 24x24 -gravity Center label:- \) -geometry 24x24+3+53 -gravity NorthWest -composite \ \( -size 24x24 -gravity Center label:- \) -geometry 24x24+3+80 -gravity NorthWest -composite \ \( -size 24x24 -gravity Center label:9 \) -geometry 24x24+3+105 -gravity NorthWest -composite \ \( -size 24x24 -gravity Center label:- \) -geometry 24x24+3+130 -gravity NorthWest -composite \ \( -size 24x24 -gravity Center label:- \) -geometry 24x24+3+157 -gravity NorthWest -composite \ \( -size 24x24 -gravity Center label:- \) -geometry 24x24+3+182 -gravity NorthWest -composite \ UNIX> bin/sudoku no magick < txt/example3.txt | sh UNIX> mv Sudoku.jpg jpg/example3-problem.jpg UNIX> bin/sudoku yes magick < txt/example3.txt | sh UNIX> mv Sudoku.jpg jpg/example3-solution.jpg UNIX>I won't explain magick. However, the mechanics of Print_Magick() are not that bad. I create a big black square, and then I plot white squares with the contents of each cell printed as labels. I use the following variables:
- Border is the number of pixels for the border around the whole puzzle.
- PPS is the number of pixels per square.
- CW is the width of the line between squares in a panel.
- PW is the extra width of the line between squares that are in different panels.
void Sudoku::Print_Magick() const
{
int PPS = 24;
int Border = 3;
int CW = 1;
int PW = 2;
int i, j, x, y;
if (Grid.size() == 0) return;
/* Make a big square, filled in with black. */
printf("magick -size %dx%d xc:Black \\\n", PPS*9+Border*2+CW*8+PW*2, PPS*9+Border*2+CW*8+PW*2);
printf(" -background White -fill Black \\\n");
x = Border;
for (i = 0; i < 9; i++) {
y = Border;
for (j = 0; j < 9; j++) {
/* This plots each small square, with the label inside. */
printf("\\( -size %dx%d -gravity Center label:%c \\)", PPS, PPS, Grid[i][j]);
printf(" -geometry %dx%d+%d+%d -gravity NorthWest -composite \\\n", PPS, PPS, x, y);
y += (PPS+CW);
if (j == 2 || j == 5) y += PW;
}
x += (PPS+CW);
if (i == 2 || i == 5) x += PW;
}
printf(" Sudoku.jpg\n");
}
|
If you like messing with pictures, I recommend magick, as it is a super-powerful program. Of course, it's beyond the scope of this class. I just include this code in case it interests you.