CS202 Lecture notes -- Vectors of Vectors

Let's suppose that I want to represent a matrix of integers in C++. The best way to do that is to use a vector of integer vectors. I will illustrate with the program src/vdm.cpp.

This program takes three command line arguments: r, c and p. It then creates a r * c "Vandermonde" matrix over the field defined by the prime number p? What's a "field?" In this case, it is the numbers 0 through p-1, where addition, subtraction and multiplication are all modulo p. Division is defined to be the inverse of multiplication, but don't worry about it, since it doesn't really matter in this lecture.

A Vandermonde matrix is one that has the value (i+1)^j, mod p in row i and column j (everything is zero-indexed). It has some very special properties concerning invertibility of submatrices, but again, we don't care too much -- we just want to create one and print it. First, so you understand a Vandermonde matrix, here is one with five rows, three columns and a prime of 17:

         Col  Col  Col
          0    1    2
         ---  ---  ---  
Row 0 |   1    1    1   
Row 1 |   1    2    4   
Row 2 |   1    3    9   
Row 3 |   1    4   16   
Row 4 |   1    5    8   

As you can see, the only time we had to do the modulo operator was for the element in row 4, column 2. That one is equal to 5², which equals 25, but we take it modulo 17, so it eight.

Take a look at the code:

/* This program creates and prints a "Vandermonde" matrix.
   The user will enter a number of rows, a number of columns, and a prime number, p.
   The Vandermonde matrix element in row i, column j is equal to (i+1)^j, mod p.
   Vandermonde matrices have interesting mathematical properties, which I won't
   go into -- if you take CS494 from me in a few semesters, you'll learn about
   some of them! */

#include <vector>
#include <iostream>
#include <cstdio>
#include <sstream>
using namespace std;

int main(int argc, char **argv)
{
  int r;                             // Number of rows
  int c;                             // Number of columns
  int p;                             // The prime number
  istringstream ss;                  // We use this to read from the command line.
  vector < vector <int> > vdm;       // The Vandermonde matrix
  int base, val;                     // We use these to calculate (i+1)^j, mod p
  size_t i, j;

  /* Error check the command line.  I usually don't like to put multiple statements
     on a single line like this, but with error checking, it's cleaner. */

  if (argc != 4) { cerr << "usage: vdm rows cols prime\n"; return 1; }
  ss.clear(); ss.str(argv[1]); if (!(ss >> r)) { cerr << "Bad rows\n"; return 1; }
  ss.clear(); ss.str(argv[2]); if (!(ss >> c)) { cerr << "Bad cols\n"; return 1; } 
  ss.clear(); ss.str(argv[3]); if (!(ss >> p)) { cerr << "Bad prime\n"; return 1; }

  /* First create all of the elements of the matrix. */

  vdm.resize(r);
  for (i = 0; i < vdm.size(); i++) vdm[i].resize(c);

  /* Next, calculate (i+1)^j mod p and put it into vdm[i][j] */

  for (i = 0; i < vdm.size(); i++) {
    base = i+1;
    val = 1;
    for (j = 0; j < vdm[i].size(); j++) {
      vdm[i][j] = val;
      val = (val * base) % p;
    }
  }

  /* Finally, print out the Vandermonde matrix. */

  for (i = 0; i < vdm.size(); i++) {
    for (j = 0; j < vdm[i].size(); j++) printf(" %4d", vdm[i][j]);
    cout << endl;
  }

  return 0;
}

To start with, take a look at the way I declare the vector of vectors:

  vector < vector <int> > vdm;       // The Vandermonde matrix

It's a good idea to separate the >'s and <'s with a space. On some copilers, ">>" is interpreted as a keyword (like with cin) and you'll get a compiler error if you omit the space. Other compilers are ok with no space -- since you never know, it's best to be safe and keep the space. I will always have the space.

We start by resizing vdm to be the number of rows. When we do that, each vector element is an empty vector. We go through each of these and resize it to be the number of columns. Now our matrix has r*c element.

Next, we set the elements by running through each row, and setting base to (i+1) and val to one. Now we calculate (i+1)^j%p by multiplying the previous element, which is (i+1)^(j-1)%p by (i+1). When we're done, we have an r * c Vandermonde matrix. The second set of for loops prints it out.

UNIX> bin/vdm 1 1 101
    1
UNIX> bin/vdm 3 3 101
    1    1    1
    1    2    4
    1    3    9
UNIX> bin/vdm 3 5 101
    1    1    1    1    1
    1    2    4    8   16
    1    3    9   27   81
UNIX> bin/vdm 3 5 7
    1    1    1    1    1
    1    2    4    1    2
    1    3    2    6    4
UNIX> 

Vectors of Vectors don't have to represent rectangular matrices

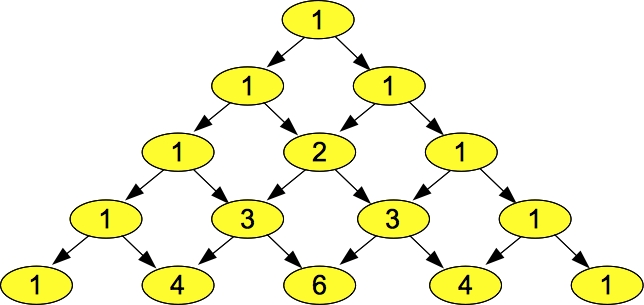The numbers are arranged in rows, where row i has i+1 elements (as always, our lives are zero-indexed). The first and last element in each row is equal to one. Each other element is the sum of the two elements above it. Suppose we want to write a program to generate Pascal's triangle in a data structure. One easy way to do this is to generate it as a vector of integer vectors, where element i of the vector is a vector containing the elements of row i. We can visualize it below:

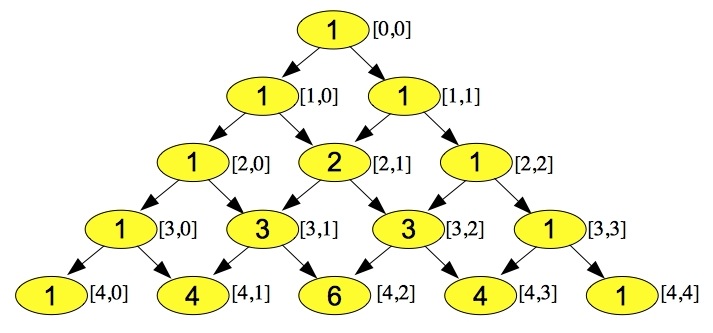Scanning for a pattern, let's consider the j-th element in row i. If it is the first or last element in the row, it will equal one. Otherwise, you can see from the picture that it is equal to the sum of elements j-1 and j in row i-1. That gives us a nice way to construct the triangle. The code is in src/pascal.cpp:

/* This program creates Pascal's triangle and prints it out.
   It stores Pascal's triangle as a vector of vectors. */

#include <vector>
#include <iostream>
#include <sstream>
#include <cstdio>
using namespace std;

int main(int argc, char **argv)
{
  int r;                               // The number of rows
  vector < vector <int> > pascal;      // The vector of vectors that holds Pascal's triangle

  size_t i, j;
  istringstream ss;

  /* Error check the command line. */

  if (argc != 2) { cerr << "usage: pascal rows\n"; return 1; }
  ss.clear();  ss.str(argv[1]); if (!(ss >> r)) { cerr << "Bad rows\n"; return 1; }

  /* Create an entry in the vector for each row.  Then add values to each row
     by using push_back() with either the value one, or the sum of two values
     on the previous row. */

  pascal.resize(r);
  for (i = 0; i < pascal.size(); i++) {
    for (j = 0; j <= i; j++) {
      if (j == 0 || j == i) {
        pascal[i].push_back(1);
      } else {
        pascal[i].push_back(pascal[i-1][j-1] + pascal[i-1][j]);
      }
    }
  }

  /* Print out the vector of vectors. */

  for (i = 0; i < pascal.size(); i++) {
    for (j = 0; j < pascal[i].size(); j++) printf(" %4d", pascal[i][j]);
    cout << endl;
  }

  return 0;
}

When we run it, it's pictured a little differently than above, but you should see that it is clearly the same triangle:

UNIX> bin/pascal 10
    1
    1    1
    1    2    1
    1    3    3    1
    1    4    6    4    1
    1    5   10   10    5    1
    1    6   15   20   15    6    1
    1    7   21   35   35   21    7    1
    1    8   28   56   70   56   28    8    1
    1    9   36   84  126  126   84   36    9    1
UNIX> 

Making Copies of Things

  vector < vector <int> > negative_pascal; // This will be a copy, and we'll negate the elements.

At the end of the program, before we print anything out, we make a copy of pascal, and then we run through it and negate all of the elements:

  /* Make a copy of pascal. */

  negative_pascal = pascal;

  /* Set each element of this to its negation. */

  for (i = 0; i < negative_pascal.size(); i++) {
    for (j = 0; j < negative_pascal[i].size(); j++) {
      negative_pascal[i][j] = -negative_pascal[i][j];
    }
  }

And we print both of them:

UNIX> bin/vcopy 5

negative_pascal = pascal;

This is blessing and a curse. It's a blessing, because it's a lot easier than creating negative_pascal with loops and push_back commands. It's a curse, because you can burn megabytes of memory with a single line of code, and poor management of memory is a speed and resource killer of computers.

So I want to you pay attention to when you make copies of things, because it is in fact so easy!