CS140 Final Exam: December 11, 2006

Answer all of these on separate sheets of paper.
Put your name and your CS email address on each sheet.

Question 1: 8 points

Below is a hash table whose size is 16. Suppose you are using linear probing. Answer the following questions:

a: Suppose you want to insert the string "Ouest", which has a hash value of 24. Into which hash table index will you insert it?
b: Suppose instead that "Ouest" has a hash value of 42. Now into which hash table index will you insert it?
c: Suppose instead that "Ouest" has a hash value of 30. Now into which hash table index will you insert it?
d: Which of the following numbers would be possible hash values for the string "Anacapri": 0, 15, 30, 45, 163, 175?
e: Finally, suppose that you are using quadratic probing insead of linear probing. Moreover, suppose instead that "Ouest" has a hash value of 15. Now into which hash table index will you insert it?

Question 2: 6 points

a: Show the results of doing a preorder printing of the following tree.
b: Show the results of doing a postorder printing of the following tree.

Question 3: 4 points

Let f(n) = 3n² + 4, and let g(n) = n². Which of the following is the correct reason why:

f(n) = O(g(n))?

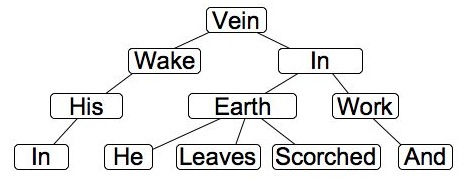
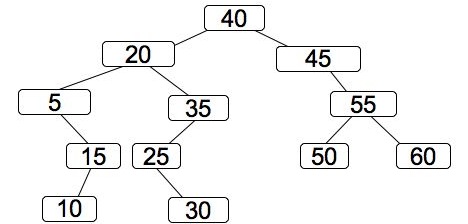
a: For all values of n, f(n) >= g(n).
b: For all values of n, g(n) >= f(n).
c: For all values of n, 4f(n) >= g(n).
d: For all values of n, 4g(n) >= f(n).
e: For all values of n, bf(n) >= g(n).
f: For all values of n, bg(n) >= f(n).
g: For all values of n > 0, f(n) >= g(n).
h: For all values of n > 0, g(n) >= f(n).
i: For all values of n > 0, 4f(n) >= g(n).
j: For all values of n > 0, 4g(n) >= f(n).
k: For all values of n > 0, bf(n) >= g(n).
l: For all values of n > 0, bg(n) >= f(n).
m: For all values of n > 10, f(n) >= g(n).
n: For all values of n > 10, g(n) >= f(n).

o: For all values of n > 10, 4f(n) >= g(n).
p: For all values of n > 10, 4g(n) >= f(n).
q: For all values of n > 10, bf(n) >= g(n).
r: For all values of n > 10, bg(n) >= f(n).
s: For all values of n > n₀, f(n) >= g(n).
t: For all values of n > n₀, g(n) >= f(n).
u: For all values of n > n₀, 4f(n) >= g(n).
v: For all values of n > n₀, 4g(n) >= f(n).
w: For all values of n > n₀, bf(n) >= g(n).
x: For all values of n > n₀, bg(n) >= f(n).
y: None of the above.

Question 4: 8 points

a: Specify exactly how you would determine whether a given tree is an AVL tree?
b: Why do we like AVL trees?

Question 5: 7 points

Behold the following tree:

a: Suppose the tree pictured is a normal binary search tree. Draw the tree that results when 20 is deleted.
b: Suppose the tree pictured is a splay tree. Draw the tree that results when 43 is inserted.
c: Suppose the tree pictured is a splay tree. Draw the tree that results when 2 is inserted.

Question 6: 9 points

Behold the following typedef of a tree:

typedef struct {
  Jval key;
  Jval val;
  Dllist children;
} Tree;

Each node may have any number of children.
Each node in children is a jval whose .v field is a (Tree *).

Write the procedure print_height(), which has the following prototype:

void print_height(Tree *t);

Print_height() should print the height of the given tree on standard output, right justfied and padded to 5 spaces. Note, the tree in Question 2 has a height of four, and the tree in Question 5 has a height of five.

Random Extra Credit Question: 1 point

The tree in Question 2 was constructed from a snippet of lyrics from a song. Who wrote the song (person or group)?

Dllist.h

#include "jval.h"

typedef struct dllist {
  struct dllist *flink;
  struct dllist *blink;
  Jval val;
} *Dllist;

extern Dllist new_dllist();
extern void free_dllist(Dllist);

extern void dll_append(Dllist, Jval);
extern void dll_prepend(Dllist, Jval);
extern void dll_insert_b(Dllist, Jval);
extern void dll_insert_a(Dllist, Jval);

extern void dll_delete_node(Dllist);
extern int dll_empty(Dllist);

#define dll_traverse(ptr, list) \
  for (ptr = list->flink; ptr != list; ptr = ptr->flink)
#define dll_rtraverse(ptr, list) \
  for (ptr = list->blink; ptr != list; ptr = ptr->blink)