CS140 Final Exam - December 10, 2019. Answers and Grading
James S. Plank
Question 1: 27 Points
- Part A: True. After either a zig-zig or zig-zag imbalance is fixed, the tree
is balanced, so you can stop.
- Part B: False. This is backward (it's the definition of big omega).
- Part C: O(n). Inserting into the middle of a deque is the same as inserting
into the middle of a vector.
- Part D: O(log n) -- that's one reason why we like AVL trees.
- Part E: O(n) -- it's an inorder traversal.
- Part F: O(n2). In a sum of expressions, it's the big O of the largest
expression, with any constant factors removed.
- Part G: O(1) -- that's one reason why we like lists.
- Part H: See part E. It's an inorder traversal.
- Part I: False. The associative array feature of a map will insert i if it's
not there. The compiler will exit with an error if you call the method const.
- Part J: True. The very definition of big O.
- Part K: O(n). The tree doesn't have to be balanced -- if we insert keys from
"A" to "Z" in that order, the tree has a depth of 26.
- Part L: O(n log(n)). In a sum of expressions, it's the big O of the largest
expression, with any constant factors removed.
- Part M: O(log m). Inserting into a multimap is O(log x) where x
is the number of elements in the multimap. Their values don't matter.
- Part N: True, because b is not modified. Now, it's a different matter as to
what happens if i is not in the map, but that's not what the question is asking.
- Part O: It has to be a postorder traversal. You'll have to call a recursive clearing
method on the two children, and then you delete the node. Please see Clear() in
the lecture notes on binary search trees. It calls a postorder method called
recursive_destroy().
- Part P: This is also postorder -- you have to calculate the expressions of the
children, before you can perform an arithmetic operator on them. Please see the
"Example Question" in the lecture notes on trees.
- Part Q: False. Although you only need one rotation to fix a zig-zig and two
rotations to fix a zig-zag, when they are fixed, you tree may still be unbalanced, so you
have to keep traversing up to the root of the try to check imbalances.
- Part R: This is O(n).
Grading:
1.5 points per part. (27 points total).
In the grading file that you receive, I used the following abbreviations:
t for True
f for False
1 for O(1)
ln for O(log n)
n for O(n)
nln for O(n log n)
ns for O(n^2)
nsln for O(n^2 log n)
15 for O(15n^2)
15+ for (O(15 n^2 + 400n + 5log n)
ns+ for O(n^2 + n + log n)
400 for O(400n)
5 for O(5 log n)
pre for Preorder
post for Postorder
in for Inorder
55 for O(55n)
55+ for O(55n + 4n log(n) + 20log n)
55- for (O(55n + n log(n) + log(n))
4 for O(4 n log n)
20 for O(20 log n)
lm for O(log m)
lnlm for O((log n)(log m))
m for O(m)
nm for O(nm)
nlm for O(n log m)
mln for O(m log n)
mlm for O(m log m)
Question 2: 20 Points
This question requires that you identify the running times of the various loops and
data structures:
- Implementation 1: x.size() is n, and
y.size() is m, and swap() is O(1). This is O(nm).
- Implementation 2: Pushing to the front of a deque is O(1), so
this is O(n).
- Implementation 3: x.size() is n, but there are only m distinct
elements of x. Therefore s will have a maximum of m elements. This
is O(n log m).
- Implementation 4: The outer loop iterates n times. The inner loop
iterates up to m times (because x's values are between 0 and m-1).
Finally, F(j) is O(j). This one is O(nm2).
- Implementation 5: The outer loop iterates n times. The inner loop
iterates (log m) times. So this is O(n log m).
- Implementation 6: Since this is a multimap, it will have up to n elements.
This is O(n log n).
- Implementation 7: The loop iterates m times. The values of y are
between 0 and n-1, and n > m. That means that the set can have up to m
elements. This is O(m log m).
- Implementation 8: The first loop is O(n). The second is O(m).
That makes O(n+m). However, we know that m is smaller than n, which
means that n+m < 2n. Since O(2n) is the same as O(n), the answer
is O(n).
- Implementation 9: Inserting into a the front of v is O(v.size()).
Therefore, this is O(n2).
- Implementation 10: Since there are ony m distinct values of x[i], there
are only m distinct values of y[x[i]]. This is O(n log m).
Grading: 2 points per correct answer. The abbreviations in the grading file
are roughly the same as above. If you saw "npx", it meant "n to the power of x".
Question 3: 20 Points
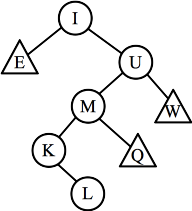
- Part A: When we insert Z, node W's children have heights of 0 and 2.
It is the lowest imbalanced node.
- Part B: When we insert R, node Q's children have heights of 2 and 1, so
it's ok. Node M's chilren have heights of 1 and 3, so it is the lowest imbalanced node.
- Part C: When we delete G, node E's children have heights of 0 and 2.
It is the lowest imbalanced node.
- Part D: When we delete C, nodes A and E are balanced. However,
node I children have heights of 2 and 4, so it is imbalanced.
- Part E: When we delete I, we replace it with G and delete G. That
makes E imabalanced (like part C). Alternatively, we could replace it with
K and delete K. That makes M imbalanced. Either answer is fine.
- Part F: L simply becomes the right child of K:
- Part G: When U is deleted, it is replaced either by the "previous"
node, S, or the "next" node, W. Here are the trees in either case:
| Replaced by S: 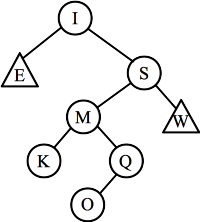
|
Replaced by W: 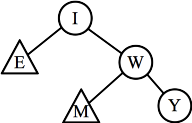
|
- Part H: When P is inserted, it makes node M imbalanced. It
is a zig-zag imbalance, so you rotate twice about O. Below left is the imbalanced
tree, and below right is after the two rotations:
| After inserting P, node M is imbalanced. 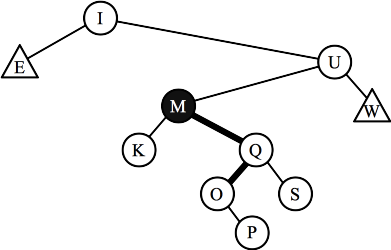
|
Rotate twice about O: 
|
- Part I: When Z is inserted, it makes node W imbalanced. It
is a zig-zig imbalance, so you rotate once about Y. Below left is the imbalanced
tree, and below right is after the rotation:
| After inserting Z, node W is imbalanced. 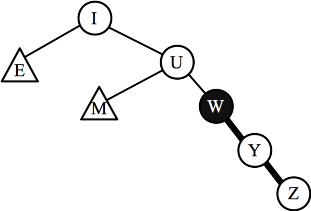
|
Rotate about Y: 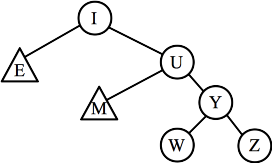
|
- Part J: When K is inserted, it makes node M imbalanced. It
fits the case where it is both a
zig-zig imbalance and a zig-zag imbalance, so you can either rotate once about Q, or
twice about O. I show both below
| After deleting K, node M is imbalanced. 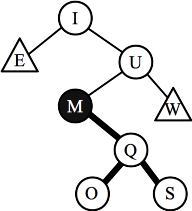
|
Rotate about Q: 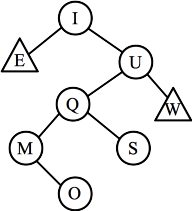
|
Or rotate twice about O: 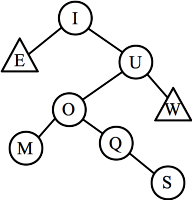
|
Grading: 2.5 points per answer.
Question 4: 17 Points
Straight from the lecture notes:
void Queue::Push(const string &s)
{
Qnode *newnode;
newnode = new Qnode; // Create the new node.
newnode->s = s;
newnode->ptr = NULL;
if (last == NULL) { // If the queue is empty, set first to be this new node.
first = newnode;
} else { // If the queue is non-empty, set the pointer of the last node to be this new node.
last->ptr = newnode;
}
last = newnode; // Finally, set last to point to the new node, and increment size.
size++;
}
string Queue::Pop()
{
Qnode *oldfirst;
string rv;
if (size == 0) throw((string) "Bad pop");
/* Move "first" to point to the next node, store the return value, and
delete the previous first node. */
rv = first->s;
oldfirst = first;
first = oldfirst->ptr;
delete oldfirst;
/* Handle the empty queue. */
if (first == NULL) last = NULL;
/* Update size and return. */
size--;
return rv;
}
|
Grading:
Each method was worth 8.5 points. Typically, you started with 8.5 and
then received deductions. Common deductions:
- Not testing for the empty queue on Push(): -2 points.
- Not incrementing size: -0.75 points
- Not decrementing size: -0.75 points
- Not setting last in Push() : -1
- Not setting first in Pop() : -1
- Not calling delete in Pop() : -3
- Returning an error rather than throwing one in Pop(): -0.8 points.
Question 5: 16 Points
As the writeup says, there are two parts of this -- building v, and then
writing rec_children(). I'm going to start with rec_children(). It will
have the following prototype:
int rec_children(const vector <int> &v, int index);
|
It will return maximum number of children of any subtree the tree that starts at index.
As with all recursive procedures, this needs a base case -- that should be when the tree is
a single node. How do we figure that out? If v[index] is equal to index+1. In
that case, we return zero.
If the tree is not a single node, then it has subtrees. We need to call rec_children() on
all of the subtrees, recording the maximum return value. At the same time, we can count the
children. We return the maximum value.
How do we identify the subtrees?
Well:
- The first one starts at index+1, and ends at v[index+1].
- The next one starts at v[index+1]+1. Call that index i. It ends at v[i].
- The next one starts at v[i]+1. And so on.
- You know you're at the end when the "next" one is a right parenthesis, and not a left
parenthesis. (There are other ways to figure that out. For example, if the "next" one's
index is v[index], you are also at the end of your children).
Here's the code for rec_children():
int rec_children(const vector <int> &v, int index)
{
int recursive_answer, nc, a;
int i;
if (v[index] == index+1) return 0; // Base case -- if it's a single node, return 0.
nc = 0; // This will hold the number of children.
recursive_answer = 0; // This will hold the maximum answer for all children.
for (i = index+1; i != v[index]; i = v[i]+1) { // Traverse the subtrees
nc++; // Use nc to count the number of children.
a = rec_children(v, i); // Compute the max children of each subtree.
if (a > recursive_answer) recursive_answer = a;
}
if (nc > recursive_answer) recursive_answer = nc;
return recursive_answer; // Return the max of children and answers for the children.
}
|
Now, the code for max_children() has to create the vector
v and then call rec_children(). To create the vector
v, we use a stack (I use a deque for that) data structure.
Whenever we see a left paren, we push its index onto the stack. When
we see a right parent, we pop its corresponding left paren off the
stack, and use that pairing to create v. Here's the code:
int max_children(const string &s)
{
vector <int> v;
deque <int> st;
size_t i, j;
v.resize(s.size(), -1); // Create v by using st as a stack
for (i = 0; i < s.size(); i++) {
if (s[i] == '(') { // Push the index onto the stack on '('
st.push_front(i);
} else { // Otherwise pop the index of the corresponding '('
j = st[0];
st.pop_front();
v[j] = i;
}
}
return rec_children(v, 0); // The answer is rec_children, starting at index 0
}
|
I've put a main() onto this code in
q5.cpp, so that you can test it. It takes the parameter string
on the command line.
The majority of you did not use a stack, but instead did something like:
- Traverse s.
- If s[i] is a left paren, then search for the corresponding right
paren. If you did this correctly, you had to count the number of left
and right parens that you have seen, so that you can find the correct
right paren.
This is an O(n2) algorithm, whereas using a stack is O(n). For that reason this answer started at 5 points rather than 8.
Grading:
I typically started at 8 points for rec_children, and then took off
deductions. Common deductions:
- "Incorrect setting/finding of the the children" - up to 3 points off.
This is when your loop to find the children was off.
- "Don't count children" - you only keep track of the max of the recursive
calls: -1
- "Don't maintain the max of the recursive calls": -1.5
For max_children(), you either started at 8 points or 5 points, depending
on whether you used the stack solution or the O(n2)
solution above. Common deductions:
- "Creating V incorrectly" - Your loop to create v was incorrect.
For example, you didn't count the left and right parens.
- "No call to rec_children": -1 point