 |
The exam was given on Canvas, and a few questions used banks. Here is an example exam that you would have gotten on Canvas.
 |
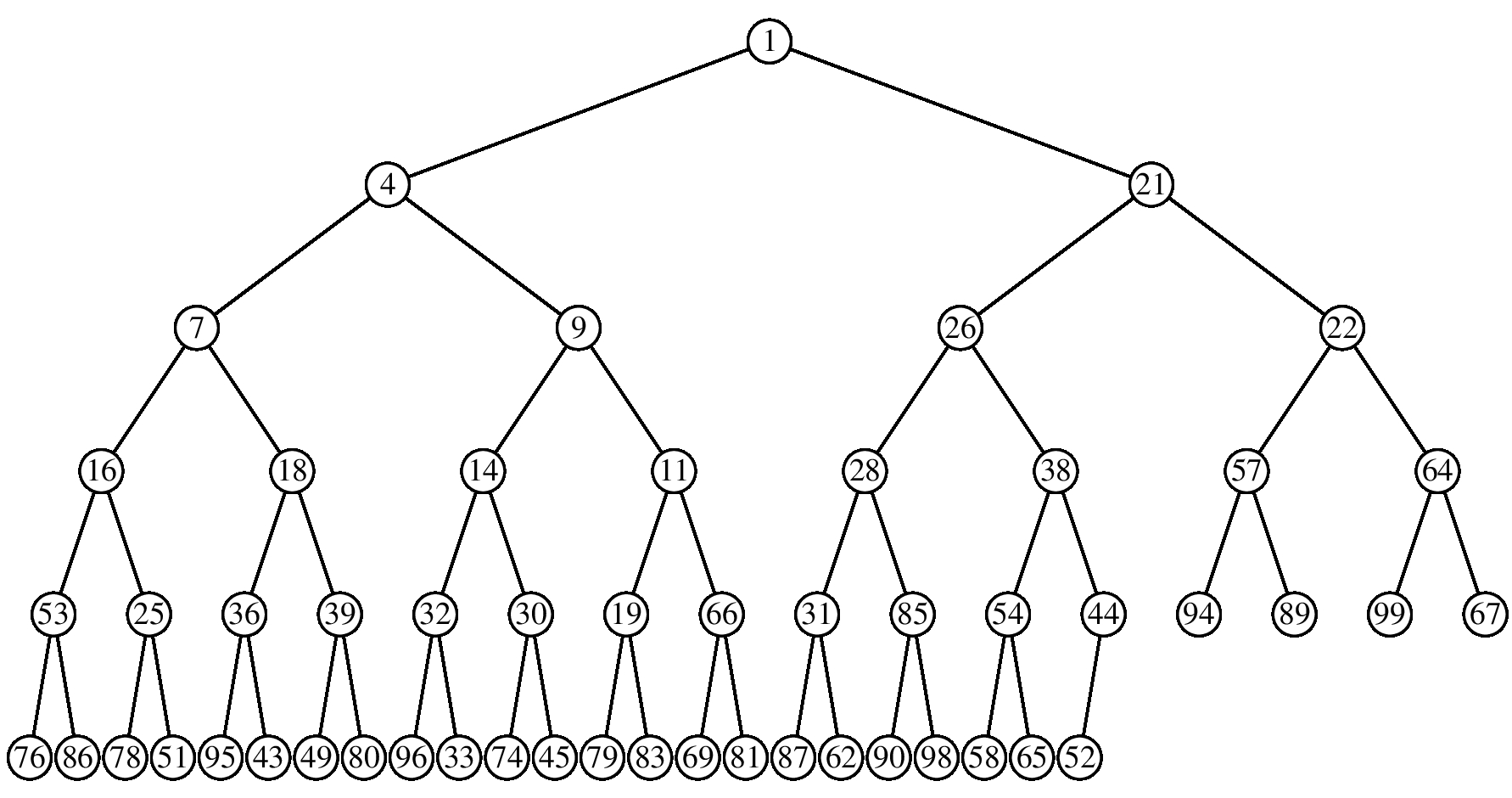
Suppose I call Push(36) on this heap.
What will the index of 36 be in the vector after the Push? ___________
What will the last value of the vector be, after the Push? ___________
 |
Suppose I call Pop() on this heap.
What will the index of 33 be in the vector after the Pop? __________
What will the first value of the vector be, after the Pop? __________
GFD L:--- R:--- GIY L:GFD R:--- HAB L:GIY R:LPH JRC L:--- R:--- LPH L:JRC R:--- PCW L:HAB R:PYB PYB L:--- R:RLB RBS L:--- R:--- RLB L:RBS R:RQH RQH L:--- R:--- SGV L:PCW R:YUA STD L:--- R:WVL WVL L:--- R:XYN XYN L:--- R:--- YUA L:STD R:---Suppose I insert LFN. What will be the key of its parent node? (Use "---" if the new node is the root) ___________
BYR L:--- R:CCX CCX L:--- R:CFT CFT L:--- R:EIN EIN L:--- R:GOX GOX L:--- R:--- ILD L:BYR R:RKO JAZ L:--- R:--- LOZ L:JAZ R:--- PIB L:LOZ R:--- RKO L:PIB R:WZV TGH L:--- R:VRU VRU L:--- R:WHA WHA L:--- R:--- WZV L:TGH R:XPQ XPQ L:--- R:---Suppose I delete the root. What will be the key of the new root? ___________
#include <vector>
class Fred {
public:
Fred();
~Fred();
Fred(const Fred &f);
Fred& operator= (const Fred &f);
// More stuff that does't matter.
protected
std::vector <int> *v;
};
|
And the following implementation of the constructor and destructor:
#include <vector>
using namespace std;
Fred::Fred()
{
v = new vector <int>;
}
Fred::~Fred()
{
delete v;
}
|
Please implement the copy constructor and assignment overload.
for (i = 0; i < s.size(); i++) v.push_back(s.substr(i));(In case you've forgotten, s.substr(i) returns the substring of s starting with the character at index i and going to the end of the string). ________
void print(const AVLNode *n, bool print_height)
{
cout << n->key;
cout << " L:" << n->left->key ;
cout << " R:" << n->right->key ;
cout << " P:" << n->parent->key ;
if (print_height) cout << " H:" << n->height;
cout << endl;
}
|
J
/ \
/ \
I M
|
J L:I R:M P:--- H:2 |
And suppose b points to the node whose key is "I". Then calling print(b, true) prints:
I L:--- R:--- P:J H:1 |
Please answer the following questions:
DBQ L:--- R:JLB P:AWD H:2 AWD L:--- R:DBQ P:--- JLB L:--- R:--- P:DBQ H:1 |
After rebalancing, suppose a points to the node whose key is AWD.
What is a->left->key? __________
What is a->right->key? __________
What is a->parent->key? __________
Suppose b points to the node whose key is DBQ.
What is b->left->key? __________
What is b->right->key? __________
What is b->parent->key? __________
RGD L:OTC R:SIE P:TND OTC L:NTD R:PRQ P:RGD H:10 PRQ L:PIH R:QME P:OTC H:9 SIE L:RQS R:SXX P:RGD H:8 NTD L:NHE R:OEV P:OTC H:8 SXX L:SQB R:TFU P:SIE H:7 RQS L:RLL R:RWS P:SIE H:7 |
To answer the following questions, don't try to draw all of the nodes. That is a waste of time, and it will indeed waste your time. Instead, draw the imbalanced node and its children. Draw the children's heights. When you look at that, you'll figure out a few more nodes to draw, and then you can answer the question.
After rebalancing, suppose a points to the node whose key is RGD.
What is a->left->key? __________
What is a->right->key? __________
What is a->parent->key? __________
Suppose b points to the node whose key is PRQ.
What is b->left->key? __________
What is b->right->key? __________
What is b->parent->key? __________
IZY L:FMS R:MGK P:ODB FMS L:DIB R:HQS P:IZY H:9 DIB L:BXK R:EOC P:FMS H:8 MGK L:KXP R:NDR P:IZY H:7 HQS L:GQD R:ICW P:FMS H:7 NDR L:MQU R:NQA P:MGK H:6 KXP L:KKK R:LPL P:MGK H:6 |
After rebalancing, suppose a points to the node whose key is IZY.
What is a->left->key? __________
What is a->right->key? __________
What is a->parent->key? __________
Suppose b points to the node whose key is FMS.
What is b->left->key? __________
What is b->right->key? __________
What is b->parent->key? __________
I want you to read the next question, which asks you to implement some methods. However, before you write that code, come back here and answer the following questions:
A. What kind of tree traversal is set_info()? __________
B. Why do I have to have the "friend" specification in Tree.hpp? Your answer should be one sentence. __________
C. Should I implement a destructor for the Tree class? Please answer yes or no. __________
D. Why? Your answer should be one sentence. __________
For the next three questions, you can answer in hexadecimal if you want.
If your answer is in hex, please put "0x" in the front of the number.
Suppose my tree is the following:
0
/|\
/ | \
4 8 3
/ \
5 7
|
9
E. What is the value of the info field for node 0? __________
#include <vector>
#include <deque>
#include <list>
#include <set>
#include <map>
#include <unordered_set>
#include <unordered_map>
#include <iostream>
using namespace std;
class TreeNode {
friend class Tree;
public:
TreeNode(int my_id);
void Print() const;
protected:
int id;
long long info;
vector <TreeNode *> children;
};
class Tree {
public:
Tree();
void Print() const;
protected:
void read_from_stdin();
void set_info(TreeNode *t, int parents_info);
void print(const TreeNode *t, int level) const;
TreeNode *root;
};
This class defines a tree, where nodes hold two values, an id
and a number called info.
The root's id will be zero, and all other node id's are unique integers.
You read a tree from standard input using the read_from_stdin() method. The format of standard input should be pairs of integers. The first integer in a pair is a node's id. The second is the node's parent's id. These can be given in any order, so, for example, the following tree:
0 /|\ / | \ 4 8 3 | 5can be represented on standard input by:
4 0 8 0 3 0 5 8or
3 0 5 8 4 0 8 0The set_info() method is initially called on the root of the tree after read_from_stdin() is called. set_info() sets the info fields of all of the nodes. The Print() method of the Tree() class should perform a postorder traversal of the tree, indenting each node's line by two times the level of the node (the root is level zero), and then calling the node's Print() method.
I know that's a mouthful. Now, in Tree.cpp, I have implemented the following things:
You may assume that standard input is in the proper format, so you do not have to do any error checking. That simplifies your life greatly, so please take advantage of it!
But before you do so, here's what I have written for Tree.cpp:
#include "Tree.hpp"
using namespace std;
TreeNode::TreeNode(int my_id)
{
id = my_id;
info = -1;
}
void TreeNode::Print() const
{
printf("%d 0x%llx\n", id, info);
}
Tree::Tree()
{
root = NULL;
read_from_stdin();
set_info(root, 0);
}
void Tree::set_info(TreeNode *t, int pinfo)
{
size_t i;
t->info = (pinfo * 2) + t->children.size();
for (i = 0; i < t->children.size(); i++) {
set_info(t->children[i], t->info);
}
}
void Tree::Print() const
{
print(root, 0);
}
And here's a really simple Test_Main.cpp that we'll use for testing:
#include "Tree.hpp"
using namespace std;
int main()
{
Tree t;
t.Print();
return 0;
}
Before I set you loose, let's look at the output of the program on the example tree
that I showed above:
UNIX> g++ Tree_Main.cpp Tree.cpp
UNIX> echo 3 0 5 8 4 0 8 0 | ./a.out
3 0xc
4 0xc
5 0x34
8 0xd
0 0x3
UNIX>
Below, implement read_from_stdin() and print(). You'll note, in Tree.hpp,
I have included all of the STL data structures that you can use.