 |
Simulation_System::Simulation_System(int argc, char **argv)
{
....
e = new Event;
e->type = DU_Maint_Begin;
e->time = mi;
e->du = dus[0];
eventq.insert(make_pair(e->time, e));
}
|
When we run it on the last set of arguments, we see the event, but it doesn't get processed since it's after the end of the simulation:
UNIX> patron_7 4 10 1.3 3650 3 5 1 1 3651 627.3349 DU_Failed 2 633.0918 DU_Repaired 2 1006.3660 DU_Failed 0 1012.6471 DU_Repaired 0 3021.4310 DU_Failed 0 3028.8040 DU_Repaired 0 3650.0000 Simulation_Over -------------------------------- Simulation Time: 3650 DU 0's state is 0 DU 1's state is 0 DU 2's state is 0 DU 3's state is 0 3651.0000 DU_Maint_Begin 0 4691.5675 DU_Failed 1 5723.1425 DU_Failed 2 6325.4670 DU_Failed 3 7670.7184 DU_Failed 0 Uptime: 14580.6 Downtime: 19.4109 -------------------------------- UNIX>We run it again with a Maintenance interval of a year, and now we exit because the event is not implemented:
UNIX> patron_7 4 10 1.3 3650 3 5 1 1 365 365.0000 DU_Maint_Begin 0 Event not implemented 2 UNIX>
void Simulation_System::schedule_next_du_maintenance(Event *e)
{
e->type = DU_Maint_Begin;
if (e->du->id == n-1) {
e->du = dus[0];
e->time += mi;
} else {
e->du = dus[e->du->id+1];
}
eventq.insert(make_pair(e->time, e));
}
void Simulation_System::Run()
{
...
du = e->du;
if (du->state == Failed) {
schedule_next_du_maintenance(e);
} else {
cerr << "Maintenance not implemented yet\n";
exit(1);
}
break;
...
}
|
Of course, when we run it, we get failure, because the first DU is functional when maintenance starts:
UNIX> patron_8 4 10 1.3 3650 3 5 1 1 365 365.0000 DU_Maint_Begin 0 Maintenance not implemented yet UNIX>However, let's tweak the parameters so that failures happen roughly every 50 days, and repair takes 100 years. That will mean that when we do maintenance, the DU's will be under repair. We'll also have the simulation last 2.5 years rather than ten. This means that we should have exactly two sets of maintenance on our system:
UNIX> patron_8 4 2.5 3 50 3 1000000 1 1 365 23.3109 DU_Failed 2 28.6091 DU_Failed 0 55.7461 DU_Failed 1 63.4527 DU_Failed 3 365.0000 DU_Maint_Begin 0 365.0000 DU_Maint_Begin 1 365.0000 DU_Maint_Begin 2 365.0000 DU_Maint_Begin 3 730.0000 DU_Maint_Begin 0 730.0000 DU_Maint_Begin 1 730.0000 DU_Maint_Begin 2 730.0000 DU_Maint_Begin 3 912.5000 Simulation_Over -------------------------------- Simulation Time: 912.5 DU 0's state is 1 DU 1's state is 1 DU 2's state is 1 DU 3's state is 1 1095.0000 DU_Maint_Begin 0 772052.9448 DU_Repaired 3 951398.4507 DU_Repaired 2 1056266.6779 DU_Repaired 1 1155040.2999 DU_Repaired 0 Uptime: 171.119 Downtime: 3478.88 -------------------------------- UNIX>Excellent.
void Simulation_System::Run()
...
case DU_Maint_Begin:
du = e->du;
if (du->state == Failed) {
schedule_next_du_maintenance(e);
} else {
e->type = DU_Maint_End;
e->time += mt;
eventq.insert(make_pair(e->time, e));
}
break;
case DU_Maint_End:
schedule_next_du_maintenance(e);
break;
}
|
We run it on the original set of parameters and see that everything works as it should -- the maintenance events each take a day, but do nothing to failure or uptime or downtime:
UNIX> patron_9 4 10 1.3 3650 3 5 1 1 365 365.0000 DU_Maint_Begin 0 366.0000 DU_Maint_End 0 366.0000 DU_Maint_Begin 1 367.0000 DU_Maint_End 1 367.0000 DU_Maint_Begin 2 368.0000 DU_Maint_End 2 368.0000 DU_Maint_Begin 3 369.0000 DU_Maint_End 3 627.3349 DU_Failed 2 633.0918 DU_Repaired 2 734.0000 DU_Maint_Begin 0 735.0000 DU_Maint_End 0 ..... 3320.0000 DU_Maint_End 2 3320.0000 DU_Maint_Begin 3 3321.0000 DU_Maint_End 3 3650.0000 Simulation_Over -------------------------------- Simulation Time: 3650 DU 0's state is 0 DU 1's state is 0 DU 2's state is 0 DU 3's state is 0 3686.0000 DU_Maint_Begin 0 4691.5675 DU_Failed 1 5723.1425 DU_Failed 2 6325.4670 DU_Failed 3 7670.7184 DU_Failed 0 Uptime: 14580.6 Downtime: 19.4109 -------------------------------- UNIX>
typedef multimap <double, class Event *> EQ;
class Dist_Unit {
public:
double lasteventtime;
double uptime;
double downtime;
DU_State state;
int id;
EQ::iterator failure_ptr;
};
|
When we insert a failure event on the , we set failure_ptr to point to the event. For example, here's a code snippet from the constructor:
...
for (i = 0; i < n; i++) {
e = new Event;
e->type = DU_Failed;
e->time = gen_weibull(beta_f, eta_f, 0.0);
e->du = dus[i];
e->du->failure_ptr = eventq.insert(make_pair(e->time, e));
}
...
|
And now, at the start of maintenance, we delete the failure event. At the end, we generate a new failure event. To test these, we print out some messages. Finally, note that we call delete on the event, because we don't reuse it like we do the other events. If we didn't delete it, our program would have a memory leak. Here's the code from Run():
case DU_Maint_Begin:
du = e->du;
if (du->state == Failed) {
schedule_next_du_maintenance(e);
} else {
ne = e->du->failure_ptr->second;
cout << "Deleting Event: ";
Print_Event(ne);
delete ne;
eventq.erase(e->du->failure_ptr);
e->type = DU_Maint_End;
e->time += mt;
eventq.insert(make_pair(e->time, e));
}
break;
case DU_Maint_End:
ne = new Event;
ne->du = e->du;
ne->type = DU_Failed;
ne->time = simtime + gen_weibull(beta_f, eta_f, 0.0);
e->du->failure_ptr = eventq.insert(make_pair(ne->time, ne));
cout << "Generating New Event: ";
Print_Event(ne);
schedule_next_du_maintenance(e);
break;
|
When we run it, we see that failure events do get deleted and regenerated properly. Interestingly, maintenance didn't eradicate all failures, as there is still one in the system:
UNIX> patron_A 4 10 1.3 3650 3 5 1 1 365 365.0000 DU_Maint_Begin 0 Deleting Event: 1006.3660 DU_Failed 0 366.0000 DU_Maint_End 0 Generating New Event: 3619.3772 DU_Failed 0 366.0000 DU_Maint_Begin 1 Deleting Event: 4691.5675 DU_Failed 1 367.0000 DU_Maint_End 1 Generating New Event: 5457.0507 DU_Failed 1 367.0000 DU_Maint_Begin 2 Deleting Event: 627.3349 DU_Failed 2 368.0000 DU_Maint_End 2 Generating New Event: 4508.9609 DU_Failed 2 368.0000 DU_Maint_Begin 3 Deleting Event: 6325.4670 DU_Failed 3 369.0000 DU_Maint_End 3 Generating New Event: 2377.7840 DU_Failed 3 734.0000 DU_Maint_Begin 0 Deleting Event: 3619.3772 DU_Failed 0 735.0000 DU_Maint_End 0 ... 3318.0000 DU_Maint_End 0 Generating New Event: 3537.7115 DU_Failed 0 3318.0000 DU_Maint_Begin 1 Deleting Event: 3738.9977 DU_Failed 1 3319.0000 DU_Maint_End 1 Generating New Event: 4242.3191 DU_Failed 1 3319.0000 DU_Maint_Begin 2 Deleting Event: 3502.8592 DU_Failed 2 3320.0000 DU_Maint_End 2 Generating New Event: 5400.5551 DU_Failed 2 3320.0000 DU_Maint_Begin 3 Deleting Event: 11064.0722 DU_Failed 3 3321.0000 DU_Maint_End 3 Generating New Event: 4246.9549 DU_Failed 3 3537.7115 DU_Failed 0 3543.2616 DU_Repaired 0 3650.0000 Simulation_Over -------------------------------- Simulation Time: 3650 DU 0's state is 0 DU 1's state is 0 DU 2's state is 0 DU 3's state is 0 3686.0000 DU_Maint_Begin 0 4242.3191 DU_Failed 1 4246.9549 DU_Failed 3 5400.5551 DU_Failed 2 9988.6965 DU_Failed 0 Uptime: 14594.4 Downtime: 5.55007 -------------------------------- UNIX>
case DU_Maint_Begin:
du = e->du;
if (du->state == Failed) {
schedule_next_du_maintenance(e);
} else {
du->state = Under_M;
du->uptime += (simtime - du->lasteventtime);
du->lasteventtime = simtime;
ne = e->du->failure_ptr->second;
delete ne;
eventq.erase(e->du->failure_ptr);
e->type = DU_Maint_End;
e->time += mt;
eventq.insert(make_pair(e->time, e));
}
break;
case DU_Maint_End:
du = e->du;
du->state = Up;
du->downtime += (simtime - du->lasteventtime);
du->lasteventtime = simtime;
ne = new Event;
ne->du = e->du;
ne->type = DU_Failed;
ne->time = simtime + gen_weibull(beta_f, eta_f, 0.0);
e->du->failure_ptr = eventq.insert(make_pair(ne->time, ne));
schedule_next_du_maintenance(e);
break;
|
Now we have a nice simulator that works on all fronts:
UNIX> patron_B 4 10 1.3 3650 3 5 1 1 365 365.0000 DU_Maint_Begin 0 366.0000 DU_Maint_End 0 366.0000 DU_Maint_Begin 1 ... 3543.2616 DU_Repaired 0 3650.0000 Simulation_Over -------------------------------- Simulation Time: 3650 DU 0's state is 0 DU 1's state is 0 DU 2's state is 0 DU 3's state is 0 3686.0000 DU_Maint_Begin 0 4242.3191 DU_Failed 1 4246.9549 DU_Failed 3 5400.5551 DU_Failed 2 9988.6965 DU_Failed 0 Uptime: 14558.4 Downtime: 41.5501 -------------------------------- UNIX>If you look at the output with no maintenance, you'll see that maintenance doesn't seem to help in terms of uptime/downtime:
UNIX> patron_B 4 10 1.3 3650 3 5 1 1 3651 627.3349 DU_Failed 2 633.0918 DU_Repaired 2 1006.3660 DU_Failed 0 1012.6471 DU_Repaired 0 3021.4310 DU_Failed 0 3028.8040 DU_Repaired 0 3650.0000 Simulation_Over -------------------------------- Simulation Time: 3650 DU 0's state is 0 DU 1's state is 0 DU 2's state is 0 DU 3's state is 0 3651.0000 DU_Maint_Begin 0 4691.5675 DU_Failed 1 5723.1425 DU_Failed 2 6325.4670 DU_Failed 3 7670.7184 DU_Failed 0 Uptime: 14580.6 Downtime: 19.4109 -------------------------------- UNIX>But, is one run really enough, especially when it generates just three failures? No.
main(int argc, char **argv)
{
int i;
long seed;
Simulation_System *ss;
double downtime, dt;
double iterations;
vector <double> simvals;
if (argc != 12) {
cerr << "usage: patron n duration(years) beta_f eta_f beta_r eta_r gamma_r maintenance_time maintenance_interval iterations seed\n";
cerr << " all other units are days\n";
exit(1);
}
if (sscanf(argv[10], "%lf", &iterations) != 1 || iterations < 0) {
cerr << "Bad iterations\n";
exit(1);
}
if (sscanf(argv[11], "%ld", &seed) != 1) {
cerr << "Bad seed\n";
exit(1);
}
srand48(seed);
downtime = 0;
ss = new Simulation_System(argc, argv);
for (i = 0; i < iterations; i++) {
ss->Run();
dt = ss->get_downtime();
simvals.push_back(dt);
downtime += dt;
}
sort(simvals.begin(), simvals.end());
printf("Iterations: %10.0lf\n", iterations);
printf("Min: %10.4lf\n", simvals[0]);
printf("Max: %10.4lf\n", simvals[simvals.size()-1]);
printf("Mean %10.4lf\n", downtime / iterations);
printf("\n");
cout << simvals[0] << " " <<
simvals[simvals.size()-1] << " " <<
downtime / iterations << " " <<
simvals[simvals.size()/2] << " " <<
simvals[simvals.size()/4] << " " <<
simvals[simvals.size()*3/4] << endl;
}
|
Unfortunately, this also requires some changing of our Simulation_System. In particular, we need to be able to call Run() many times for different runs. This means that Run() needs to re-initialize the simulator's state. We do that by implementing a new method called Initialize_Simulation(), which resets all of the simulator's state, including deleting the event queue:
void Simulation_System::Initialize_Simulation()
{
int i;
Event *e;
Dist_Unit *du;
EQ::iterator eqit;
while (!eventq.empty()) {
eqit = eventq.begin();
e = eqit->second;
delete e;
eventq.erase(eqit);
}
for (i = 0; i < n; i++) {
du = dus[i];
du->lasteventtime = 0;
du->uptime = 0;
du->downtime = 0;
du->state = Up;
}
e = new Event;
e->type = Simulation_Over;
e->time = duration;
e->du = NULL;
eventq.insert(make_pair(e->time, e));
for (i = 0; i < n; i++) {
e = new Event;
e->type = DU_Failed;
e->time = gen_weibull(beta_f, eta_f, 0.0);
e->du = dus[i];
e->du->failure_ptr = eventq.insert(make_pair(e->time, e));
}
e = new Event;
e->type = DU_Maint_Begin;
e->time = mi;
e->du = dus[0];
eventq.insert(make_pair(e->time, e));
}
|
We remove the relevant code from the constructor, and call Initialize_Simulation() at the beginning of Run(), and that allows us to run the simulation a bunch of times:
Let's first run the simulation one iteration with a few different seeds:
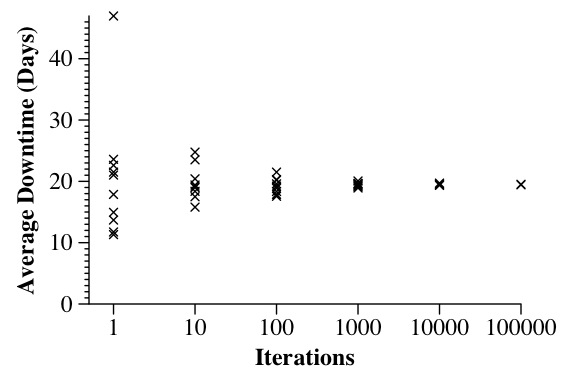
UNIX> patron_C 4 10 1.3 3650 3 5 1 1 3650 1 0 Iterations: 1 Min: 19.4109 Max: 19.4109 Mean 19.4109 19.4109 19.4109 19.4109 19.4109 19.4109 19.4109 UNIX> patron_C 4 10 1.3 3650 3 5 1 1 3650 1 1 Iterations: 1 Min: 21.0263 Max: 21.0263 Mean 21.0263 21.0263 21.0263 21.0263 21.0263 21.0263 21.0263 UNIX> patron_C 4 10 1.3 3650 3 5 1 1 3650 1 2 Iterations: 1 Min: 17.8684 Max: 17.8684 Mean 17.8684 17.8684 17.8684 17.8684 17.8684 17.8684 17.8684 UNIX>Those value differ by quite a bit, so if we are going to try to draw conclusions, we'll need to make multiple runs. To assess this, the following graph shows the results of ten runs for each of the given number of iterations:
 |
Clearly, using fewer than 1000 iterations does not give you a good average value. Were I trying to publish this data, I'd be using at least 100,000 iterations per data point. You should also be wary about just presenting average numbers. The following graph compares the two strategies of doing no maintenance and doing yearly maintenance:
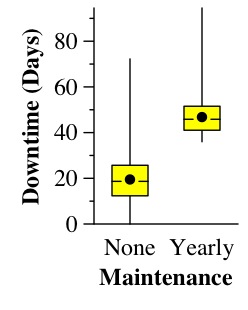 |
The plots are called Tukey plots. They convey much more information than a simple average value. Instead, they show the spread of values from the minimum to maximum. Additionally, there is a yellow box that starts at the end of the first quartile of data, and goes to the end of the third quartile. Also shown are the mean (depicted by a dot) and the median (depicted by hash marks inside the box. The Tukey plots are effective at showing that no maintenance is much better on average than maintenance. It is true that an individual run with no maintenance may show more downtime than an individual run with maintenance. But the average behavior of using no maintenance is clearly better.
Exploring further, perhaps we'd like to see how different maintenance intervals impact the average downtime. The following graph plots this information:
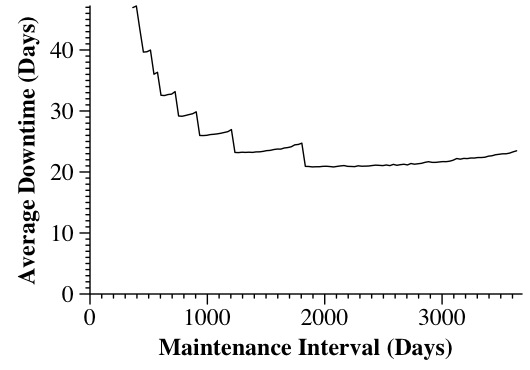 |
There are a few problems with this graph. First, I'm plotting days on the X axis. Is that what I want? No -- I tend to think about maintenance in terms of yearly intervals, so I should change the X axis to plot the interval in terms of years. Second, where is the point for no maintenance? It's not there, and it should be. I fix both problems below (I include this because many people will write papers and give me graphs like the one above, because they are easy to produce, rather than take the time to modify them so that they are easy to read):
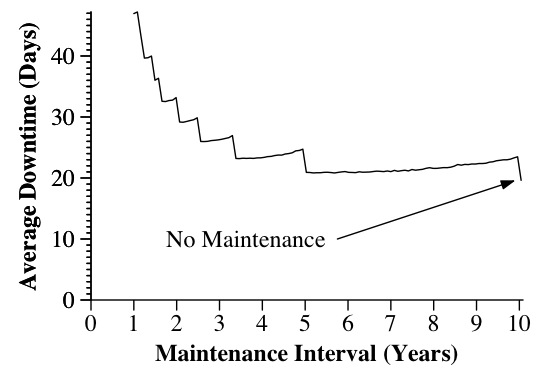 |
Much better. Now, why the steps in the curve? The reason is that each step downward represents one fewer maintenance operation. For example, when the interval is between five and ten years, there is just one maintenance operation. When the interval is between 3.4 and five years, there are two. Each maintenance interval adds significant downtime to the simulation. However, if you look just at the curve when there is only one maintenance interval, you'll see that there is less downtime on the five year side than there is on the ten year side. Why? Because both perform the same amount of maintenance, but when maintenance is performed just after five years, that helps to prevent failures from five to ten years. When maintenance is performed just before ten years, you don't prevent any of the failures from five to ten years, but you still absorb the maintenance overhead. Regardless, performing no maintenance gives you the smallest amount of downtime.
Our next exploration is to see what happens when the maintenance time is reduced. The following graph plots the downtime of performing yearly maintenance when the maintenance time ranges from a little more than an hour to a day:
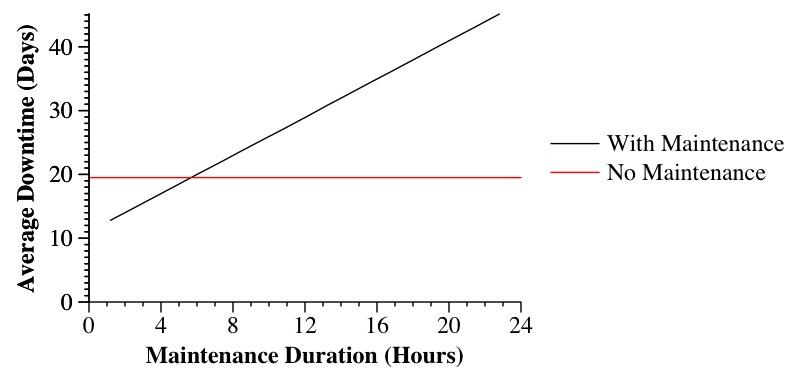 |
The graph shows that when the maintenance time is sufficiently small (less than 5.5 hours or so), that yearly maintenance results in less average downtime than no maintenance.
How about messing with βf? Does this impact performance? We plot the results below:
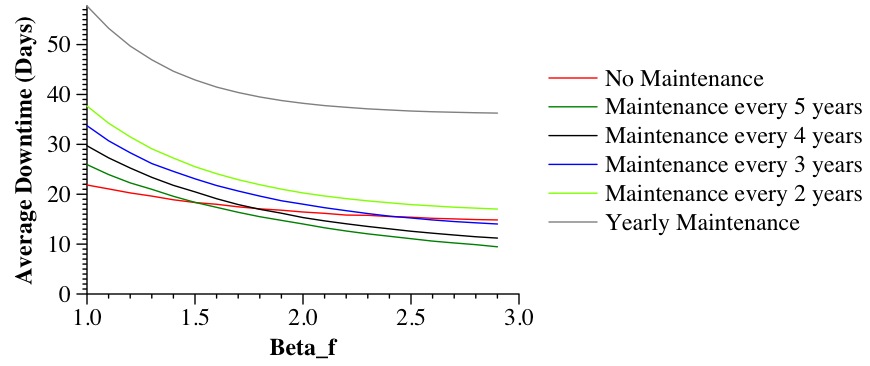 |
βf most definitely impacts the effectiveness of maintenance. Increasing βf makes maintenance more effective. Why? Because increasing βf shifts the random numbers so that they are closer to the mean -- there are fewer small random numbers, so there are fewer failures generated before scheduled maintenance.
One implication of this is that you need to have confidence that the parameters of your simulation match what you're trying to simulate. If you use βf equal to 1.3, but in reality it is 3, then you will draw incorrect conclusions from your simulation. How do you assure that you have the right parameters? We'll talk about it in class (It's certainly outside the scope of this class, but something that you should think about. You'd be amazed how much academic research gets published that draws conclusions based on simulation parameters that have no justifiable basis in fact....)