CS302 -- Final Exam. March 13, 2008 -- Answers and Grading Guide

Question 1 - 6 Points

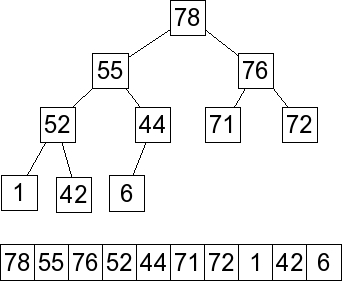
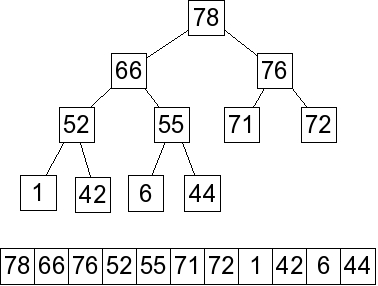
Part A: Below we show the priority queue as an array and as a linked data structure:

When we delete the maximum element, we replace it with the last element in the array, which is 6:

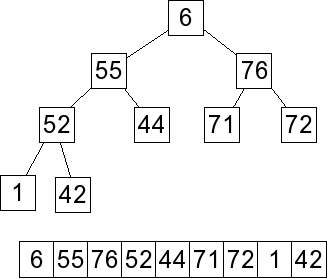
Now we percolate down -- the 6 will be swapped with 76 and 72 to yield the following -- the array version is the answer to part A:

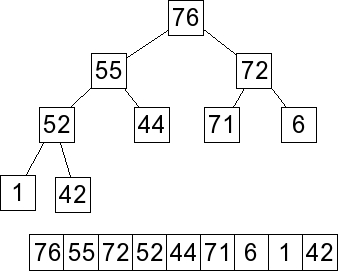
Part B: Now, to add an element, we put it as the last element in the array:

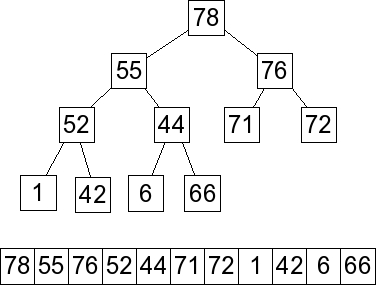
And we percolate up -- here is the final answer:

Grading

Three points for each part. If you percolated, but incorrectly, you received one and a half instead of three points for each part. If you simply deleted 76 and added 66 to the end without doing anything else, you received zero.

Question 2 - Ten Points

Grading

1 point per question -- no partial credit.

Question 3 - 8 Points

You need two procedures -- the main merge_sort() which allocates a second temporary array and calls a recursive merge sort, and the recursive merge sort, which calls itself recursively on the first and second halves of the array, and then calls merge() to merge the two together. Here it is -- you could have used new instead of malloc(): merge.cpp 

void do_merge_sort(double *a1, double *a2, int size)
{
  int middle;
  
  if (size == 1) return;
  middle = size/2;

  do_merge_sort(a1, a2, middle);
  do_merge_sort(a1+middle, a2, size-middle);
  merge(a1, middle, a1+middle, size-middle, a2);
  for (i = 0; i < size; i++) a1[i] = a2[i];
}

void merge_sort(double *a, int size)
{
  double *a2;

  a2 = (double *) malloc(size*sizeof(double));
  do_merge_sort(a, a2, size);
  free(a2);
}

Grading

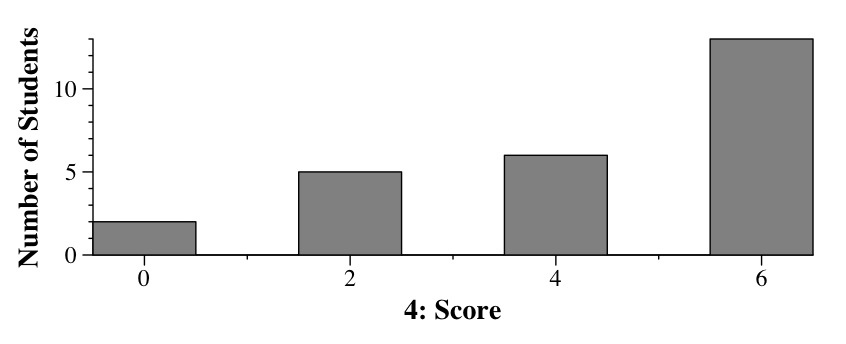
Question 4 - 6 Points

The answers are A, C and D.

B is not possible, because you need to print out the children of "You" before "Me". E is not possible, because you need to print out the children of "Don't" before "Me". F is not possible, because you need to print out the children of "Babe" before "Free".

Extra Credit: The song is "You Keep Me Hangin' On", originally a Motown hit for the Supremes in 1966. I can't say that the version I had in mind was that one, but the cover by Wilson Pickett, which is worth the buck on Itunes/Amazon if for no other reason than the beginning, where the bass does a brilliant disconnect from the rest of the band.

In 1986, Kim Wilde made a dance-oriented remix, which is how most people remember the song, and while the remix is good for what it is, Kim doesn't even attempt to communicate the pain and suffering that the good Mr. Pickett is exhibiting.

Other covers were also made by Rod Stewart, Malanie Safka, Reba McEntire and Vanilla Fudge (a 60's band, not to be confused with 80's industry creation Vanilla Ice....). Wikipedia tells me that American Idol contestants have covered the song at least four separate times.

Grading - 6 Points

Half a point if you got the song, full point if you got any of the artists.

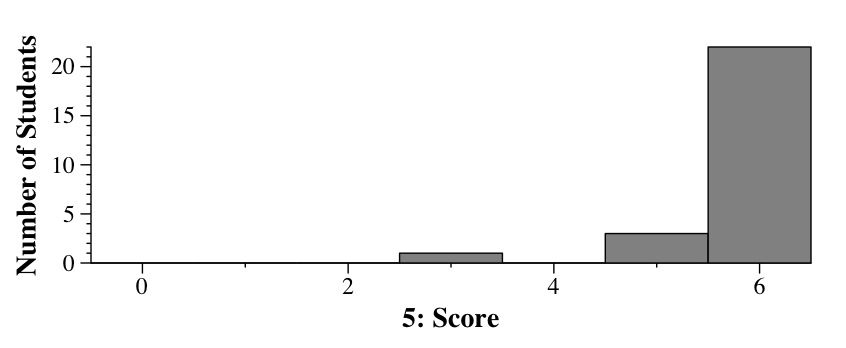
Question 5 - 6 points

This program reads pairs of first names and last names. When it reads a name it checks to see if the last name is in the map. If so, it adds the first name to the fns set associated with the last name, and prints out that the first name was added. If the last name is not in the map, then it creates an instance of the LNames class, puts the first name into the set and and adds it to the map. When the instance o the class is created, a line is printed saying that the last name was created.

Here's the output: 

UNIX> prog < input.txt
Created Woods with James
Added Ickey to Woods
Created Austin with Woody
Added Tiger to Woods
Created Woodpecker with Woody
Added Steve to Austin
Created Herman with Woody
UNIX>

Grading

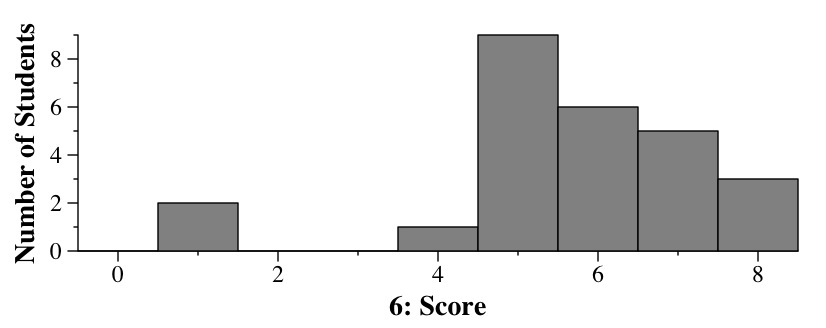
Question 6: 8 Points

This is a straightforward nested traversal, in a6.cpp: 

void print_all_names(LNMap *ln)
{
  LNMap::iterator lnit;
  LNames *l;
  set <string>::iterator sit;

  for (lnit = ln->begin(); lnit != ln->end(); lnit++) {
    l = lnit->second;
    for (sit = l->fns.begin(); sit != l->fns.end(); sit++) {
      cout << l->lname << ", " << *sit << endl;
    }
  }
}

Grading

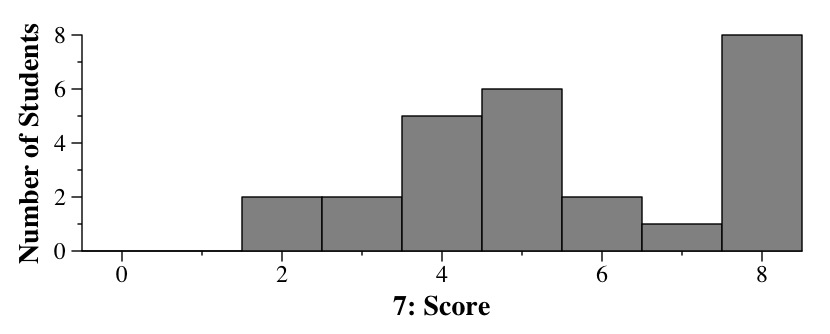
Question 7 - 8 Points

A CDF defines a probability distribution and works as follows -- CDF(x) is a number from zero to one, and denotes the probability that a random number chosen according to the distribution is less than or equal to x.

As such, CDF(x) must be a number between zero and one, and if x' > x, then CDF(x') must be ≥ CDF(x).

Part A: If x is greater than or equal to three, then CDF(x) will be greater than one, which is impossible. Hence, we restrict its value.

Part B: This means that the probability of generating a number less than one according to this distribution is 1/9.

Part C: If d: The probability of b is 1/9. The probability of c is 4/9-1/9 = 1/3, and the probabiliby of d is 1 - 4/9 = 5/9. Outcomes a and e cannot happen.

Part D: To generate a random number, we need to start with the equation

drand48() = x2/9

And solve it for x:

drand48() = x2/9
9*drand48() = x2
sqrt(9*drand48()) = x
3 * sqrt(drand48()) = x

Therefore, q is the correct answer.

Grading