CS302 Midterm, Spring, 2017

James S. Plank

Answers and Grading

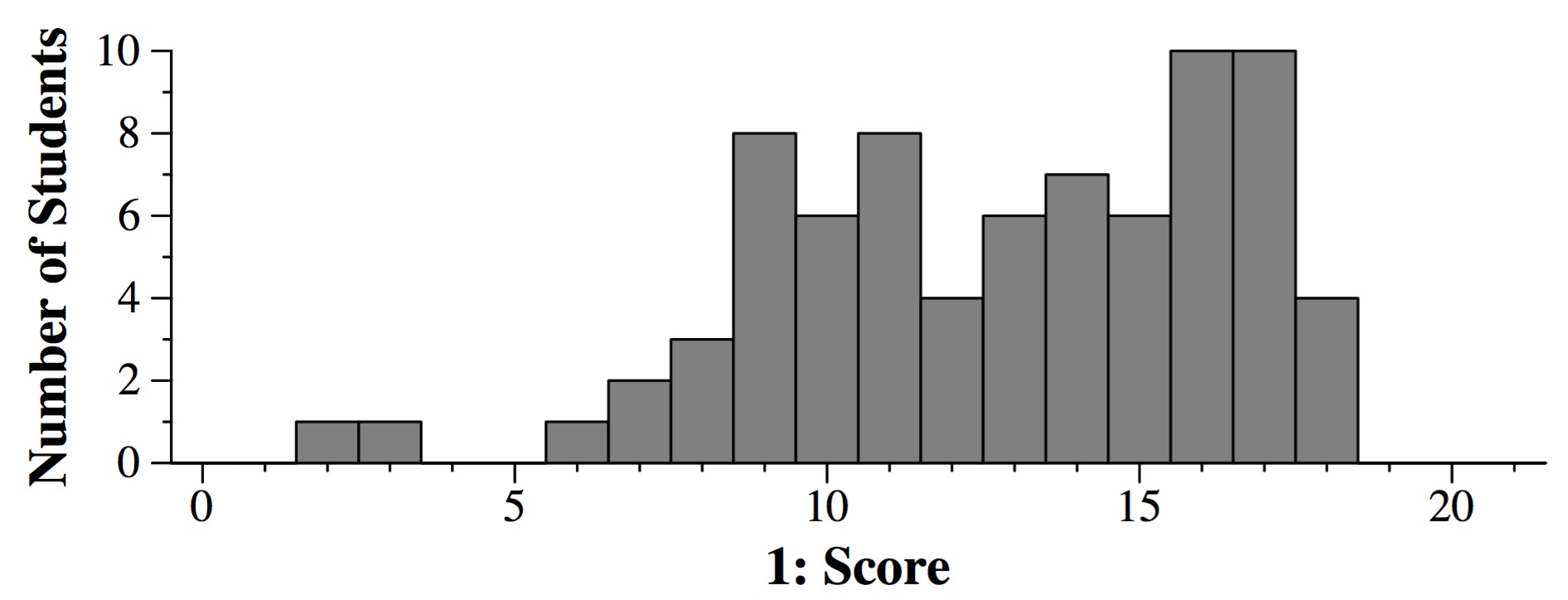
Question 1: 21 points

• Part A: (89.6%) From the lecture notes -- this is linear O(n).
• Part B: (66.2%) Each Pop() is O(log(n)), so this is O(m log(n)).
• Part C: (80.5%) O(n log(n)), plain and simple.
• Part D: (63.6%) Merge sort is always the same: O(n log(n)).
• Part E: (37.3%) You can find the element with upper_bound(). That is O(log(n)). Then you'll increment an iterator m times, which is O(m). Since we know that m is greater than log(n), this is O(m).
• Part F: (70.1%) When n is even, element n/2 is one that has no children -- it's on the bottom of the heap. Therefore, Percolate_Up() must go from the bottom to the top of the heap: O(log(n)). When n is odd, then n/2 is one level from the bottom. Percolate_Up() is still O(log(n)).
• Part G: (61.0%) Quicksort's worst case is O(n²).
• Part H: (57.1%) From the lecture notes: O(m α(n)).
• Part I: (61.0%) From the lecture notes: O(m).
• Part J: (7.8%) See part F: We are either on the bottom level, or one up from the bottom level. In each case Percolate_Down() will be constant time: O(1).
• Part K: (44.2%) This is O(n) plus O(log(n)). Since O(log(n)) is smaller than O(n), their sum is simply O(n).
• Part L: (76.6%) This is the following code for multiset s and vector v:

    for (sit = s.begin(); sit != s.end(); sit++) v.push_back(*sit);
  

  That is linear: O(n).
• Part M: (68.8%) Merge sort is always the same: O(n log(n)).
• Part N: (54.5%) The median-of-three algorithm handles this case nicely, and works in Quicksort's best case: O(n log(n)).
• Part O: (97.4%) Insertion sort's worst case is O(n²).

Grading: 1.4 points per part. I gave some partial credit, but not a large amount.

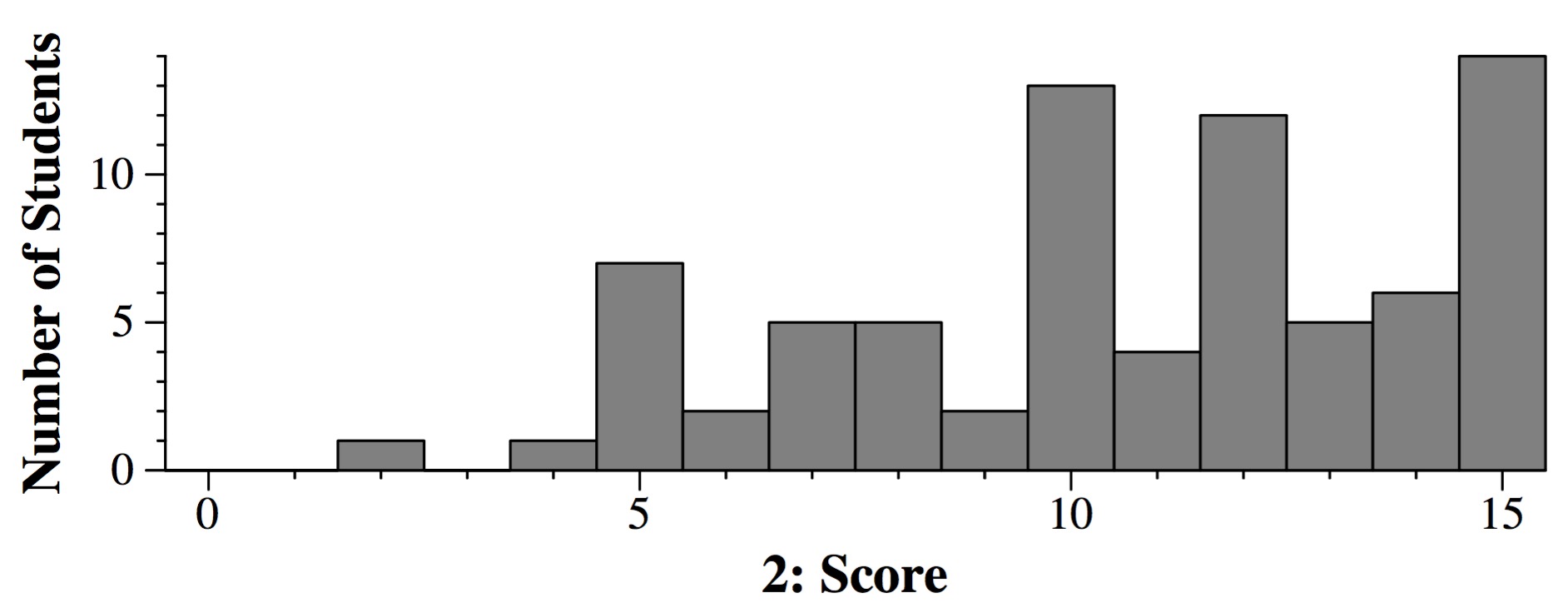
Question 2: 15 points

• Part A: (92.2%) The answer is the number of permutations of the cities: 12!
• Part B: (68.8%) The number of 10-character strings from a 5-character alphabet: (X%) 5¹⁰.
• Part C: (81.8%) "12 choose 5", which is equal to "12 choose 7": (12!) / ( (5!) (7!) )
• Part D: (48.1%) That's a power set enumeration: 2⁶.
• Part E: (66.2%) This is the number permutations of the 15 balls: 15!
• Part F: (40.3%) This is the number of ways to choose 5 elements from 23 elements: "23 choose 5", which is equal to "23 choose 18": (23!) / ( (5!) (18!) )

Question 3: 25 points

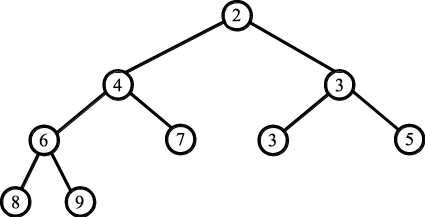
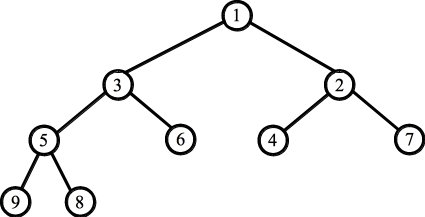
• Part A: (89.6%) Here's the tree before and after the push operation:

  The answer is: { 1, 2, 3, 6, 4, 3, 5, 8, 9, 7 }

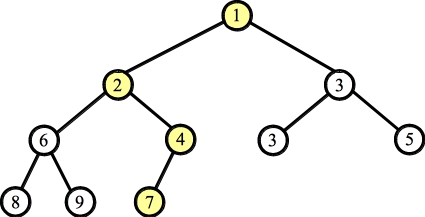
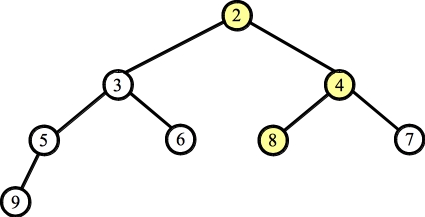
• Part B: (59.7%) Here's the tree before and after the pop operation:

  The answer is: { 2, 3, 4, 5, 6, 8, 7, 9 }

• Part C: (55.8%) This will swap 0 and 5, and then 1 and 6: { 0, 1, 3, 6, 2, 8, 5, 4, 7}

• Part D: (48.1%) Depending on whether you start the outer for loop, this will sort the first four or five elements of D fortunately, the result is the same: { 0, 2, 4, 5, 6, 1, 3, 8, 7 }

• Part E: (66.2%) This is the median of 7, 5 and 6: The answer is 6

• Part F: (54.5%) You will swap 6 and 4, and 8 and 1. After that, the partitioned vector is { 5, 0, 4, 2, 1, 3, 7, 8, 6 }. That's two swaps.

• Part G: (33%) You will swap 6 and 2, and 8 and 6, and then 6 and 4. After that, the partitioned vector is { 6, 2, 0, 6, 4, 6, 8, 7, 2 }. That's three swaps.

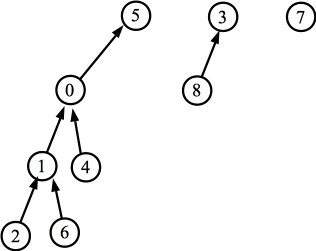
• Part H: (81.8%) Here's the data structure.

  The answer is:

  i    set-id
  -    ------
  0       5
  1       5
  2       5
  3       3
  4       5
  5       5
  6       5
  7       7
  8       3
  

• Part I: The (31.1%) ranks vector changes if the two sets have the same rank, so the answer is 7 and 3.

• Part J: (18.2%) The head of the heap is its maximum value. That means that element 7 starts the "sorted vector" part of the vector, and that element 6 ends the heap. The answer is 7 (elements 0 through 6).

Question 4: 15 points

To code this up, first sort s, and then do a power set enumeration to enumerate subsets. For each element in a subset, append it to a string, and after each subset, print the string and clear it. The answer is in q4.cpp, which has a main() that calls OSA with the command line argument:

#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cstdlib>
using namespace std;

void OSA(string s)
{
  string a;
  int i, j;

  sort(s.begin(), s.end());

  for (i = 0; i < (1 << s.size()); i++) { 
    a.clear();
    for (j = 0; j < s.size(); j++) {
      if (i & (1 << j)) a.push_back(s[j]);
    }
    cout << a << endl;
  }
}

int main(int argc, char **argv)
{
  if (argc != 2) { fprintf(stderr, "usage: q2 string\n"); exit(1); }
  OSA(argv[1]);
  return 0;
}

Grading: 15 points.

Question 5: 14 points

int Disjoint::Find(int element)
{
  vector <int> q;
  int i;

  while (links[element] != -1) {
    q.push_back(element);
    element = links[element];
  }
  for (i = 0; i < q.size(); i++) links[q[i]] = element;
  return element;
}

Recursion is even easier -- if you're the set id, you're done. Otherwise, call Find() recursively on your link field, and set your link field to the result:

int Disjoint::Find(int element)
{
  if (links[element] == -1) return element;
  links[element] = Find(links[element]);
  return links[element];
}

Grading: 7 points per implementation.

Question 6: 10 points