CS302 Midterm, Fall, 2018

James S. Plank

Answers and Grading

Question 1: 20 points

I have the number of correct answers listed (out of 56).

Snippet 1: (30) Find() is inverse Ackerman, and Union() is O(1), so the answer is O(r α(n)).
Snippet 2: (51) The constructor is linear, and Union() is is O(1), so the answer is O(n).
Snippet 3: (46) Both insert() and Pop() are O(log(n)), so the answer is O(n 2(log(n))), which is O(n log(n)).
Snippet 4: (49) This is linear, plain and simple: O(n).
Snippet 5: (20) The body of the inner loop is O(1). The outer loop iterates O(n) times, and the inner loop iterates O(log(r)) times, so the answer is O(n log(r)).
Snippet 6: (39) This is the sum of i from one to n: O(n²) .
Snippet 7: (26) The outer loop iterates O(2^m), and the inner loop iterates O(r), so: O(r 2^m).
Snippet 8: (44) upper_bound is O(log(n)) so this is our favorite: O(n log(n)).
Snippet 9: (41) Push() is O(log(n)), so this is O(r log(n)).
Snippet 10: (47) The cool part of heaps is the fact that you can construct them from an unsorted vector in linear time: O(n).

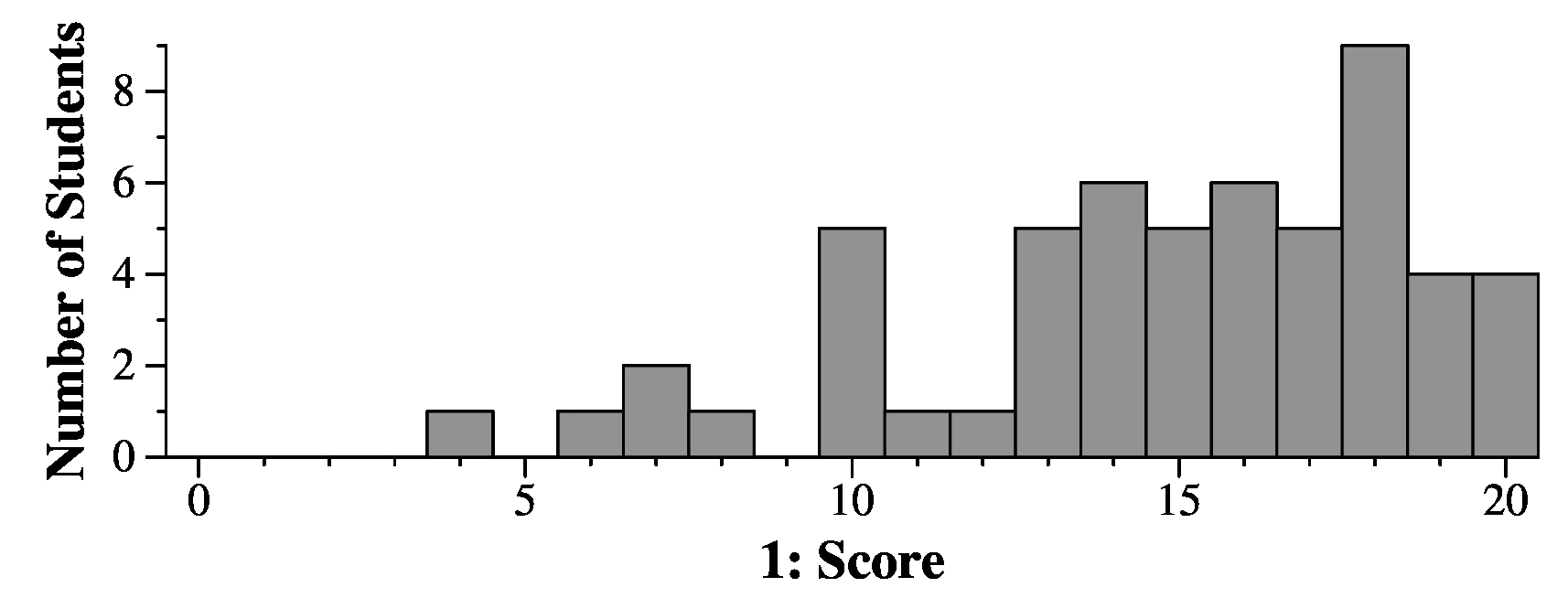
Grading: 2 points per part. I gave some partial credit. In the grading, I abbreviated, so an answer of "n" is reallly O(n). Abbreviations which may not be as clear:

2m - O(2^m)
2mr - O(2^mr)
2n - O(2ⁿ)
2r - O(2^r)
ar - O(α(r))
ln - O(log(n)) (similarly "lln, lr, nln, nlr, nlnln")
ms - O(m²)
n2m - O(n2^m)
ns - O(m²)
rar - O(r α(r))
ran - O(r α(n))
ms - O(r²)

Question 2: 32 points

In the answers, I'll show the whole vector, but I'll boldface the changed items, and color them red.

Part 1: (48) Let's convert the vectors to trees:
Convert to Tree: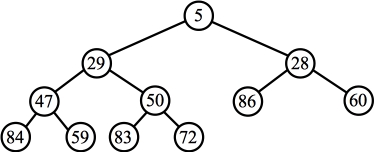
Add 3 as the last node: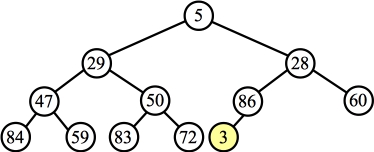
Percolate Up: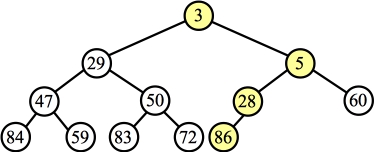

The answer is:
3 29 5 47 50 28 60 84 59 83 72 86
Part 2: (45) Again, let's convert to trees:
Convert to Tree: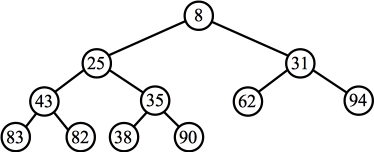
Delete the last node and move it to the root: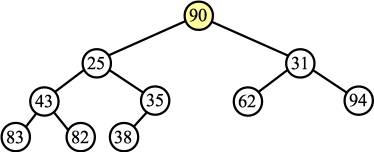
Percolate Down: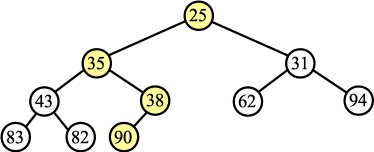

The answer is:
25 35 31 43 38 62 94 83 82 90
Part 3: (33) Again, let's convert to trees:
View unsorted vector as a tree: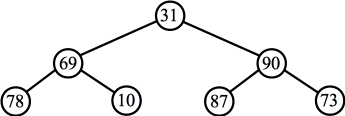
Percolate down with 69 and 90: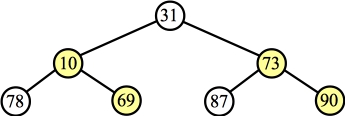
Percolate down with the root: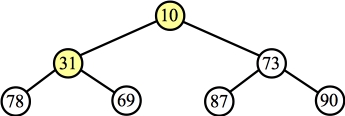

The answer is:
10 31 73 78 69 87 90
Part 4: (42) Find(9) returns 0. Find(10) returns 1. Set 1's size is greater than set 0's, size, so 0 becomes the child of one. There are only two changes: Links[0] becomes 1, and Sizes[1] becomes 9.
Node: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Links: 1 -1 0 1 1 -1 1 -1 11 0 1 -1 11 -1 0 -1 Sizes: 4 9 1 1 1 1 1 1 1 1 1 3 1 1 1 1

Part 5: (15) Find(14) returns 16. Find(8) returns 23, and as it passes through nodes 4 and 13, it sets all of their links to 23 (of course, node 13's link was already 23). Since the rank of set 23 is higher than the rank of set 16, node 23 becomes the parent of node 16. The end result is that the links entries 8, 4 and 16 all get set to 23. The ranks are unaffected, because the rank of set 23 does not change.

Node:    0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
Links:  23 11 16  0 23 23 23 23 23 13 13 23 23 23 16 10 23 23 19 13  4  7 23 -1 -1
Ranks:   2  1  1  1  2  1  1  2  1  1  2  2  1  3  1  1  2  1  1  2  1  1  1  4  1

Part 6: (37) Straightforward -- here is the original, and the first two iterations:

 80  64  61  66  47  4  51  56  40  3 
 64  61  66  47  4  51  56  40  3  80 
 61  64  47  4  51  56  40  3  66  80

Part 7: (43) The first iteration swaps 12 and 87. The second swaps 40 and 77. The third swaps 46 and 54:
12 40 46 92 77 54 59 82 87 83
Part 8: (36) This simply sorts the first four elements (or the first five, if you start the loop with i = 1). Fortunately, both have the same output:
13 60 73 85 88 62 9 10 65 86

Grading: 4 points per part. The shorthand in the grading is to enter your answers as numbers separated by slashes, with dashes for values that don't change. If your answer ends with dashes, I don't include them.

Question 3: 16 points

There were two points of this question:

The first point was not to understand what g() does, but instead to simply map the function's definition to a recursive implementation.
The second was to do some bit arithmetic. The two tasks here come straight from the bit arithmetic lecture notes, under the headinds "Clearing a Bit", and "Checking to see if bit x is set". the power set enumeration that we've gone over many times does that latter operation as part of the enumeration.

The answer is below -- please see the comments for an explanation of each part:

int g(int x) 
{
  int y, z, gz;

  /* Start with the base case. */

  if (x == 0) return 1;

  /* Find y using bit arithmetic. since x <= 1024, the 10th bit is the highest
     one that can be set, so start with y = 11. */

  for (y = 11; y >= 0; y--) {
    if (x & (1 << y)) {

      /* At this point, you have found y. You can calculate z by either
         "clearing" the bit with and-not, or simply by subtracting (1 << y): */

      z = x - (1 << y);   // This works too:   z = x & ( ~(1 << y) );
 
      /* Make the recursive call, and return the result. */

      gz = g(z);
      return y * (gz + z);
    }
  }

  /* You didn't have to do this, but if x is not in the right range, let's return -1. */

  return -1;
}

Grading: 16 points. You got 4 points for getting the base case right, and four points for the recursion. The remainder of the points were on the bit arithmetic.

Question 4: 16 points

This is a classic div/mod enumeration, from the lecture notes on enumeration. The first part of that section says, "The first type of enumeration is a problem where you have an array of size l, and each element of the array can have one of n values (repetitions are fine)." In this problem, l is the variable n, and n is four.

Here's the code, commented with what's going on:

#include <iostream>
#include <cstdio>
using namespace std;

int main()
{
  long long n;
  long long top;
  long long val, i, copy;
  string dna = "ACGT";

  cin >> n;

  /* First calculate 4^n */

  top = 1;
  for (i = 0; i < n; i++) top *= 4;

  /* Enumerate every value from 0 to 4^n-1 */

  for (val = 0; val < top; val++) {

    /* Make a copy, and treat copy as a number
       in base four -- extract each digit, which
       will be a value from 0 to 3, and use it to
       print the character of the DNA sequence. */

    copy = val;
    for (i = 0; i < n; i++) {
      printf("%c", dna[copy%4]);
      copy /= 4;
    }
    printf("\n");

  }
  return 0;
}

Grading: 16 points. You got a point for reading n, three points for calculating 4^n correctly, three points for your loop, two points for copying the loop variable so that you could do the div/mod enumeration, 6 points for the div/mod/character extraction, and one point for printing.

Question 5: 16 points

You've seen this problem before, twice. The first is in the Keno "Lucky Loser" bet, from the lecture notes on upper_bound(). Second is when I went over the topcoder problem HungryCowsEasy in class. In fact, this problem is pretty much exactly HungryCowsEasy, where the cows are cars and the barns are restaurants.

The strategy is to make a map of the restaurants, where the key is the position and the val is the number of occupants. Then, for each car, you call upper_bound() or lower_bound(), to find the restaurants whose positions are the closest greater than or less than (or equal to) the car. Update the occupants in the closer restaurant. At the end, print out the map.

You should sentinelize the map, so that there's a restaurant far less than the smallest, and far greater than the greatest. Then you don't need to worry about what happens when lower_bound() returns end() or begin().

The code is in q5.cpp. I've just included Occupants(). The code has a main() with the example from the problem writeup.

#include <map>
#include <vector>
#include <iostream>
#include <cstdio>
using namespace std;

void Occupants(vector <double> &Rpos,   // Positions of the restaurants
               vector <double> &Cpos,   // Positions of the cars
               vector <int> &Cocc)      // Occupants of the cars
{
  map <double, int> R;                  // Key = position, val = # occupants 
  map <double, int>::iterator hit;
  map <double, int>::iterator lit;
  int i;

  /* Put each restaurant, with zero occupants, into the map. */

  for (i = 0; i < Rpos.size(); i++) R[Rpos[i]] = 0;

  /* Sentinelize the map with two fake restaurants.  One should
     have a value so small that a car will never go to it, and one
     should have a value so big that a car will never go to it. */

  R[-30000] = -1;
  R[30000] = -1;

  /* For each car, find the closest restaurant whose position is less, 
     and the closest restaurant whose position is greater than or equal
     to the car.  Put the occupants from the car into the restaurant. */

  for (i = 0; i < Cpos.size(); i++) {
    hit = R.lower_bound(Cpos[i]);
    lit = hit;
    lit--;
    if (hit->first - Cpos[i] < Cpos[i] - lit->first) {
      hit->second += Cocc[i];
    } else {
      lit->second += Cocc[i];
    }
  }

  /* Print out the restaurants.  Ignore the two sentinels. */

  for (hit = R.begin(); hit != R.end(); hit++) {
    if (hit->second != -1) {
      printf("%9.2lf %d\n", hit->first, hit->second);
    }
  }
}

Grading: 16 points. You got four points for creating the map correctly, two points for lower-bound (or upper-bound), four points for the comparison of each car to two restaurants, two points for handling the edge cases, and four points for your ending loop.