2022 COSC 302 Midterm: Questions, Answers and Grading Guide

Question 1 : 15 points

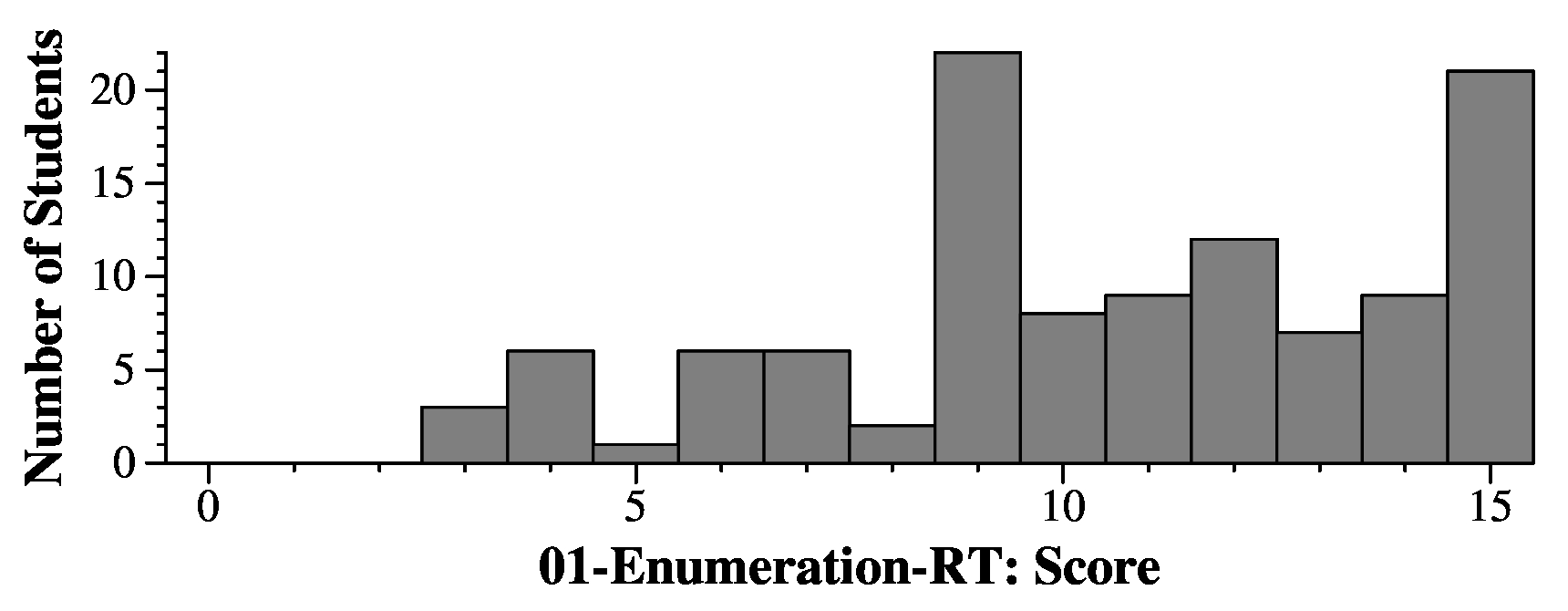
These came from a bank. You can see an example in Exam.pdf. Here are answers for those questions:

Part A: There are 26⁵ ways to have 5 lower-case letters, and 10⁴ ways to have four single numeric digits. Therefore, the answer is: (26⁵)(10⁴).

Part B: This is equal to the number of 6 digit numbers in base 17: (17⁶).

Part C: 17 choose 5, plain and simple: C(17,5) or C(17,12).

Part D: This is equal to the number of permutations of the colors: (11!).

Part E: This is the power set of the juices: (2¹²).

Grading: Three points per. You lost 0.25 points if you didn't follow the instructions, and gave me, for example (17!)/(5!12!) instead of C(17,12). I gave some partial credit, but not a huge amount.

Question 2 : 15 points

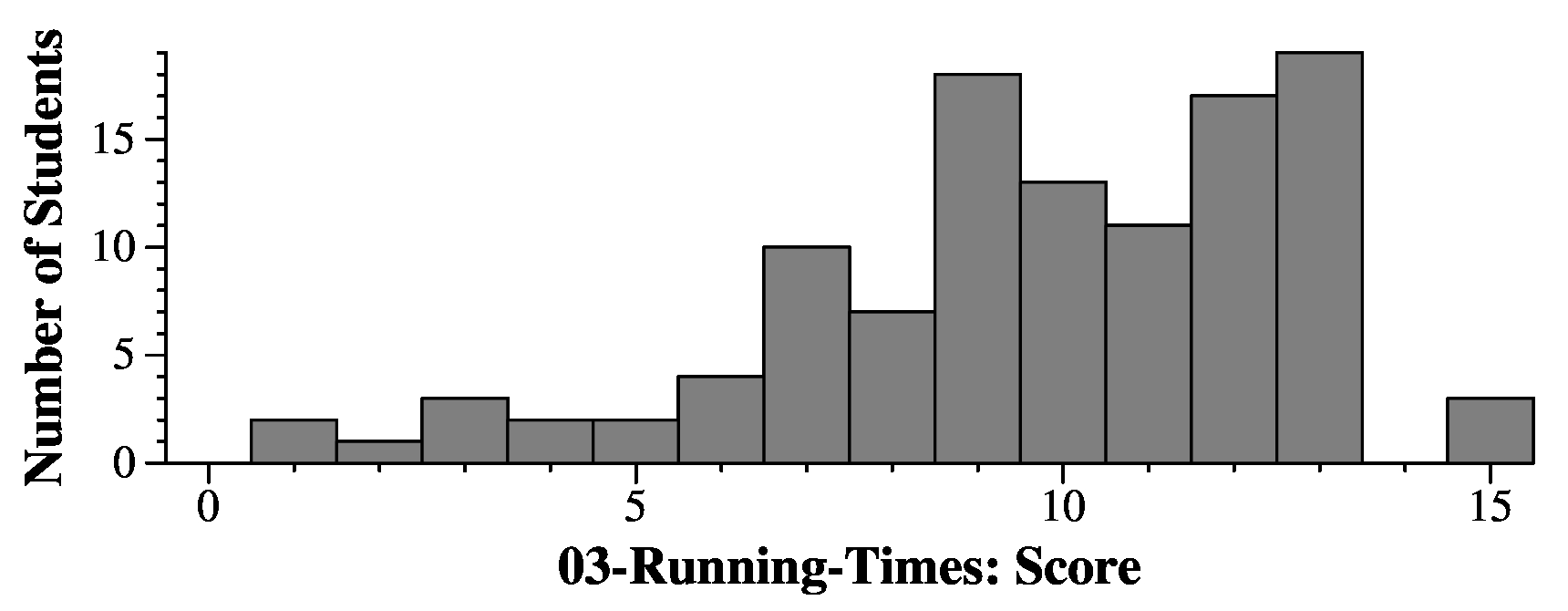
These came from a bank. You can see an example in Exam.pdf. Here are answers for those questions:

Part A: Since node 5's links is -1, it is the root of a set. Nodes 6, 12 and 18 link to node 5, so they are in the set. Node 8 links to 18, and node 19 links to 6, so those are also in the set. That's it. The answer is: 5 6 12 18 8 19 (They can be specified in any order).

Part B:

• Find(7) returns 6, because the links go 15, 21, 6, -1.
• Find(18) returns 0, because the links go 0, -1.
• Find(23) returns 23, because its link is -1.
• Find(14) returns 20, because the links go 1, 20, -.1

Part C: When we call Find(1), the links go 5, 17, 8, -1. Therefore, we change the links for 1 and 5, and their values change to 8. 17's value doesn't change.

Grading

Part B was worth 1.5 points per question.

Part C -- each node was worth 1 point and the final question was worth 1 point. You were deducted 0.5 points if you gave three nodes, and 1 point if you gave four nodes. You were deducted 2 points if you gave more than four nodes.

In the grading, if you see something like "2-19", it means that your answer was 19, and you were test #2 in the bank. Typically, you only see that on incorrect answers.

Questions 3-12

• p_b8ca2 - O(n)
• p_d9450 - O(m log n)
• p_014aa - O(m)
• p_5a7e8 - O(n log n)
• p_77587 - O(n)
• p_1ea1f - O(m alpha(n))
• p_07659 - O((log m)(log n))
• p_c3b36(strings) - O(nm)
• p_37089 - O(n^2)
• p_c3b36(map) - O(n log n)

Question 13

void binstrings(int n, int index, string &sofar)
{
  if (index == n) {
    cout << sofar << endl;
    return;
  }
  sofar[index] = 'A';
  binstrings(n, index+1, sofar);

  sofar[index] = 'B';
  binstrings(n, index+1, sofar);
}

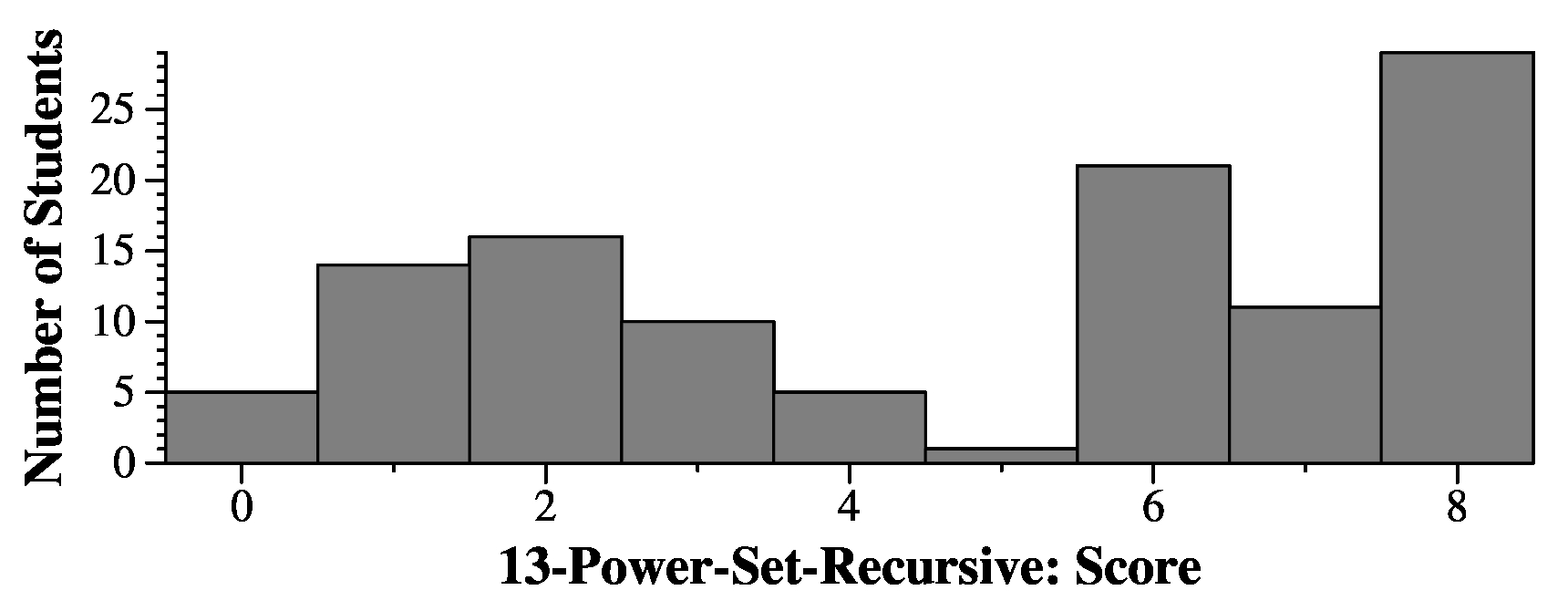
Since I already resized sofar, you can simply set the characters, rather than doing push_back() and pop_back(). Doing push_back() and pop_back() is wrong because of the resizing in main().

Grading

If your grade says "See The Answer", then your program was not structured correctly.

Question 14

void enum_cd(int n)
{
  int i, j, k;

  for (i = 0; i < (1 << n); i++) {
    for (j = 0; j < n; j++) {
      if (i & (1 << j)) printf("C"); else printf("D");
    }
    printf("\n");
  }
}

Here's the Div/Mod:

void enum_cd(int n)
{
  int top, i, j, k;

  top = (1 << n);

  for (i = 0; i < top; i++) {
    j = i;
    for (k = 0; k < n; k++) {
      printf("%c", 'C' + j%2);
      j /= 2;
    }
    printf("\n");
  }
}

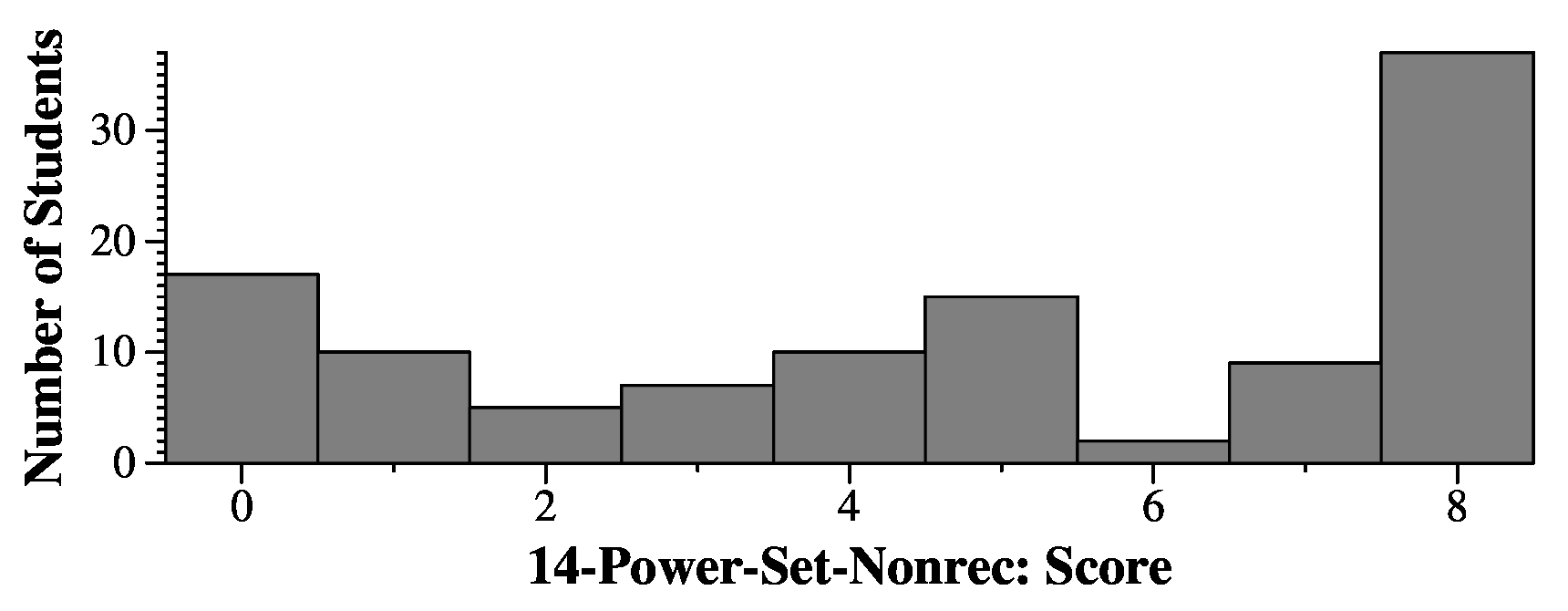
Grading was 8 points, and I took off deductions. The most common deductions were on the div/mod enumerations, where you would div and mod by n rather than two. If your grading file says "Please see the answer", then your code didn't have the right structure for either enumeration.

Question 15

#include <string>
#include <map>
#include <vector>
#include "collection.hpp"
using namespace std;

class MyImp : public Collection {          // This says it is a subclass of Collection
  public:
    void Add_Item(int id, const string &item);    // And these implement the virtual methods
    void Print();
  protected:
    map < int, vector <string> > Clxn;   // Here's the protected data
};

You also need to implement Add_Data() and Print(). Add_Data() simply adds the thing to the vector in the id's map entry:

void MyImp::Add_Item(int id, const string &item)
{
  Clxn[id].push_back(item);   // You can be more complex, but this does everything you need.
}

Print is a simple nested for loop:

void MyImp::Print()
{
  map <int, vector <string> >::iterator cit;
  size_t i;

  for (cit = Clxn.begin(); cit != Clxn.end(); cit++) {
    cout << cit->first << ":";
    for (i = 0; i < cit->second.size(); i++) {
      cout << " " << cit->second[i];
    }
    cout << endl;
  }
}

Grading

• Defining MyImp to be a subclass of Collection: 3 points
• Defining Add_Data() and Print() as public methods in the definition of MyImp: 2 points
• Defining your data structure to be protected or private: 1 point
• Your implementation of Add_Data(): 3 points. You lost points here if you used the wrong data structure. For example, if you used a:

  map <int, string>

  Then you lost two points for inserting the thing into the map. This is because you need to store multiple things for each id.

• Your definition of Print(): 5 points. Again, you lost points if you had the wrong data structure (like the example in Add_Data() above.