2022 COSC 302 Midterm: Questions, Answers and Grading Guide

October 17, 2023.
James S. Plank

Again, the answers here are to the example exam. Please see that for information about using question banks, etc.

Comments on the labels in the grading files

In the grading files, I use the following labels:

01-Running-Times: Questions 1-15
02-Enumeration-RT: Question 16 (the five-part question)
03-Inheritance: Question 17
04-Disjoint-Sets: Question 18
05-Bit-Arithmetic: Question 19
06-Binary-Search: Question 20

I have histograms for questions 1-15 after Question 15.

Question 1 (proc_1e961): 2 points

My goal here was to make you think about implementation. Since every Union() is with node 0, the maximum height of a node will be 2. For example, if you do:

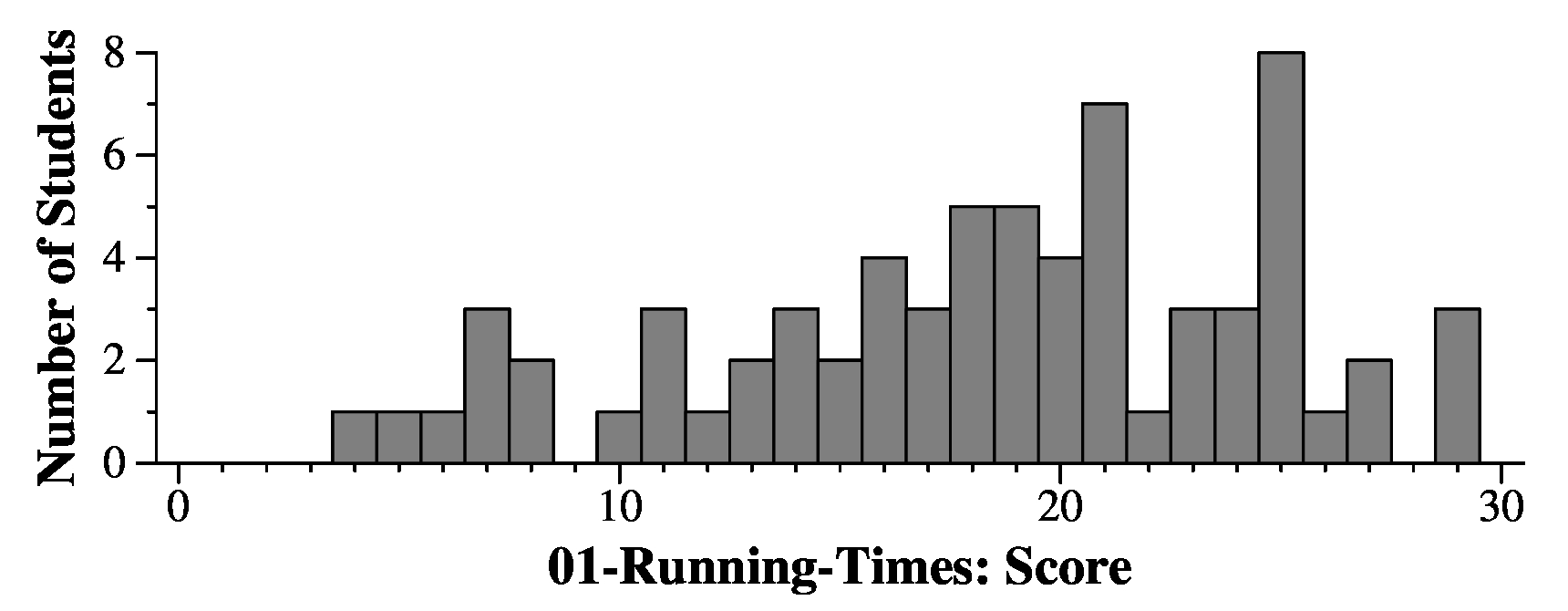
Union(0, 1);
Union(Find(0), 2);
Union(Find(0), 3);

Then your tree is going be either:

So the performance will be:

Initialize(): O(n).
First loop: O(n).
Second loop: O(n).

The answer is O(n). Some of you had exams with typos that went:

if (v[i]) d->Union(0, i);

In that case, you'll either get the first picture above, or you'll get an error with the Union() call, because 0 is not a set it.

For that reason, I gave full credit for O(n) "Error". I did not give gredit to O(1) (for exiting prematurely with an error), because the Initialize() call is O(n). I gave 1.8 points for O(alpha(n)). Even though it's not correct, I'm giving it "nearly" full credit, because the typo may have been confusing.

Question 2 (proc_cc0ad): 2 points

This inserts n different elements into the map: O(n log n).

Question 3 (proc_592f7): 2 points

The first loop is O(n). Since all of the elements of f are between 0 and 5, f's maximum size is 6, so the second loop is O(1). Thus, the answer is O(n).

Question 4 (proc_6bb2e): 2 points

E is a map, which does not store duplicate values. So e's maximum size is 6, which means that e.insert() will be O(1). The answer is O(n).

Question 5 (proc_b3229 #1): 2 points

This is a pretty classic O(n²) loop.

Unfortunately, both this and problem 11 were named proc_b3229(), so I call this one "proc_b3229 #1", as it has one argument. I call problem 11 "proc_b3229 #2".

Question 6 (proc_a9e99): 2 points

The multimap stores duplicate values, so this is O(n log n).

Question 7 (proc_9c940): 2 points

Traversing the map is O(m) and each push_back() is O(1). This is O(m).

Question 8 (proc_6db03): 2 points

This is an example of how you misuse a map. You really want to use upper_bound() here, which would be O(n log m). However, because you are traversing the map to find where the element would go, you potentially traverse the entire map each time. So the answer is O(nm).

Question 9 (proc_8eaf7): 2 points

This is the same initial loop as proc_1e961 above, which is O(n). Again, some exams had a typo, which was:

    if (v[i]) d->Union(0, i);

That would either run to completion as node 0 would be the root of the set, or it would print an error. Regardless, the Initialize() code is O(n), so the answer is O(n).

Question 10 (proc_a018f): 2 points

This is an example of misusing a map. You should say:

z.push_back(x->second);

Then the loop will be O(m). Instead, because "x[nit->first]" calls x.find(), the push_back() call is O(log m). So the answer is O(m log m).

Question 11 (proc_b3229 #2): 2 points

Each push_back() and push_front() is O(1). Since b's size is n, the answer is O(n).

Question 12 (proc_7d81c): 2 points

Straight from the lecture notes: O(n*alpha(n)).

Question 13 (proc_5eca9): 2 points

The insert() operations on the unordered_map are each O(1), so this is a straightforward O(n).

Question 14 (proc_28066): 2 points

b's size will be increased by a maximum of 6 elements, so each of the insert() operations is O(log m). The answer is O(n log m).

Question 15 (proc_da9ac): 2 points

The first for loop iterates 2n times. The second one iterates n times. So this is O(n2ⁿ).

Question 16 : 15 points

These came from a bank. These answers are for the example exam.

Part A: There are 26⁵ ways to have 5 lower-case letters, and 10⁴ ways to have four single numeric digits. Therefore, the answer is: (26⁵)(10⁴).

Part B: This is equal to the number of 6 digit numbers in base 17: (17⁶).

Part C: 17 choose 5, plain and simple: C(17,5) or C(17,12).

Part D: This is equal to the number of permutations of the colors: (12!).

Part E: This is the power set of the juices: (2¹²).

Grading: Three points per. You lost 0.25 points if you didn't follow the instructions, and gave me, for example (17!)/(5!12!) instead of C(17,12). I gave some partial credit, but not a huge amount.

Question 17 : 15 points

Here's a great answer I received from a student exam: "In scenario 1, since A is only an interface for B and C, A will define common procedures/methods that B and C will implement on their own, but A will not define any member variables, this will be left up to the individual definitions of the B and C classes.

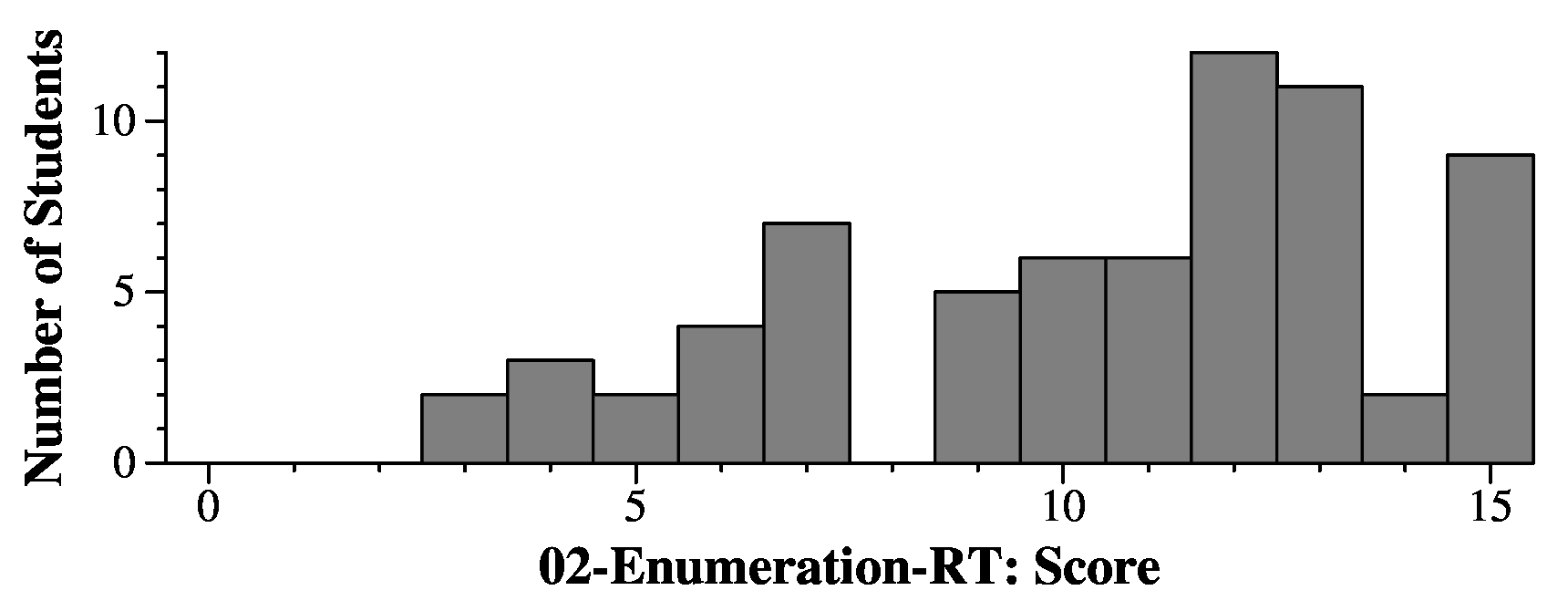"In scenario 2, since we are told inheritance is employed, this means that the super class A will define at least one member variable that B and C will each have as part of their subclass. A could also define common procedures for B and C, but what makes it inheritance is the member variable definition being in the super-class and not the individual sub-classes.

"Scenario 2 (inheritance) will lead to problems over the lifetime of a software project as it makes it very difficult to modify what the member variables of your sub-classes are. Suppose as you get farther along in a project, you decide that a sub-class could me made more efficient by changing one of its inherited member variables to a different type. Inheritance demands that you now have to go and modify the definition in the super-class and update every sub-class's implementation to match, instead of being able to keep the change local to the specific sub-class you were trying to optimize in the first place."

Grading

I allocated 10 points to the description of the two scenarios, and then 5 points for explaining why it can be a problem.

Question 18: 7 points

Straight from the lecture notes:

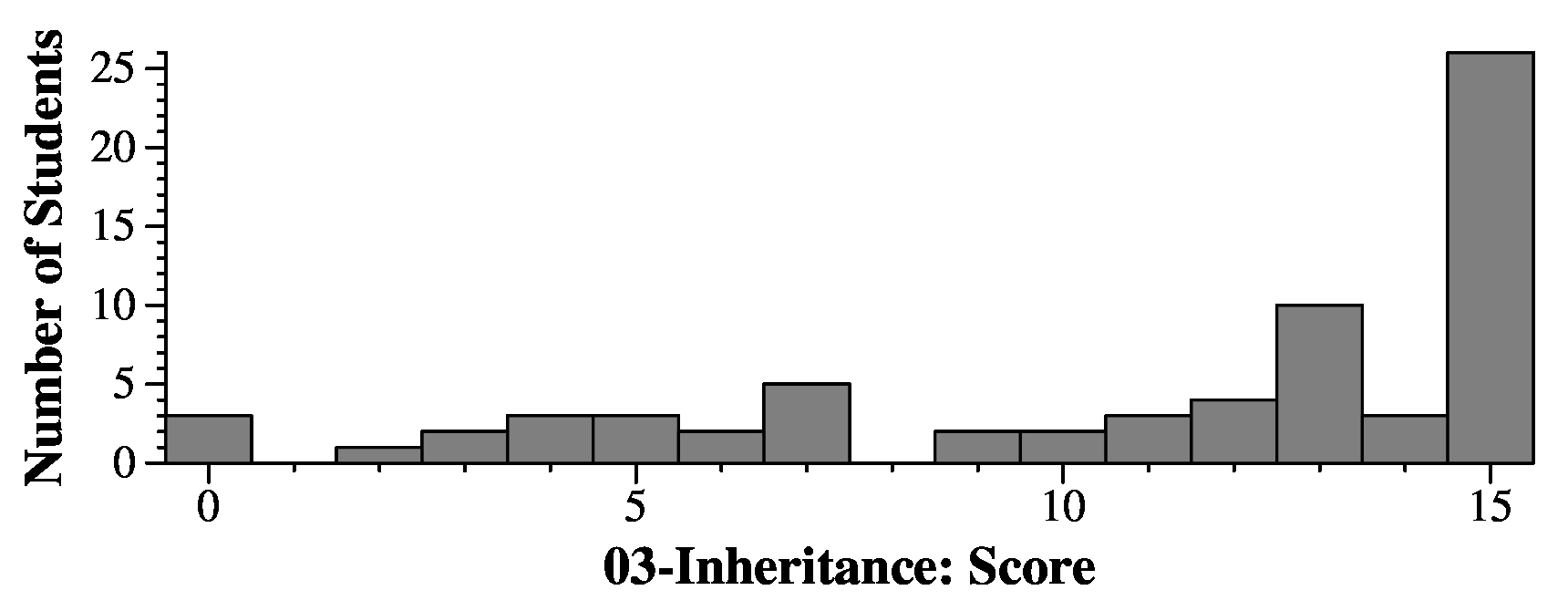int DisjointSetByRankWPC::Find(int e)
{
  vector <int> nodes;
  size_t i;

  while (links[e] != -1) {
    nodes.push_back(e);
    e = links[e];
  }

  for (i = 0; i < nodes.size(); i++) links[nodes[i]] = e;
  return e;
}

A recursive solution is even simpler:

int DisjointSetByRankWPC::Find(int e)
{
  if (links[e] == -1) return e;
  links[e] = Find(links[e]);
  return links[e];
}

Grading Notes

Most questions were graded by starting with 7 points and taking off deductions. Some answers simply say "Please see the answer." That means your code was so far off that I give you a point or two for doing something that resembles the right answer.

If you lost points for "convoluted structure", then your code may have worked, but the structure was convoluted enough to be illogical or at the very least quite hard to read. Here's an example:

int DisjointSetByRankWPC::Find(int e)
{
  vector <int> nodes;
  size_t i;
  bool done;
  int next_node;

  done = false;
  while (done == false) {
    next_node = links[e];
    if (next_node == -1) 
      for (i = 0; i < nodes.size(); i++) nodes[i] = e;
      return e;
    }
    if (links[e] != -1) {
      nodes.push_back(e);
    }
    if (next_node != -1) {
      e = next_node;
    }
  }
}

Let me show the things here that make the code hard to read:

Your loop should be while(1) or while(true). You never change the done variable.
On a more minor note, "while(!done) makes more sense that while(done == false).
You switch between using links[e] and next_node, when they are the same thing. Just use one or the other.
Frankly, you should simply have nodes.push_back(e) and e = next_node in an else clause for the first if statement.

I know coding on an exam is hard, but at least you get to type with Canvas, so you can spend the time to make the code clean.

Question 19: 8 points

There are a bunch of ways to do this, but they pretty much all boil down to testing each bit of v and then setting the appropriate bit of the return value. Here are two examples:

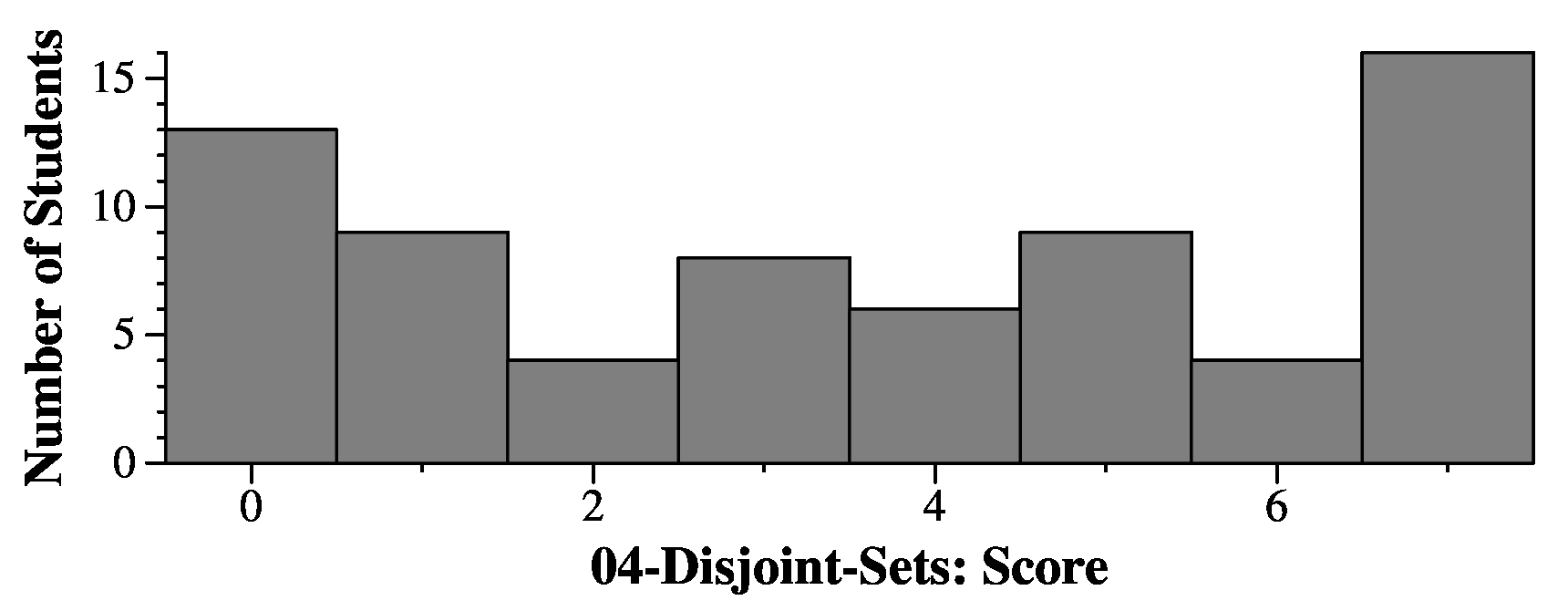unsigned int reverse(unsigned int v)
{
  int rv, i;

  rv = 0;
  for (i = 0; i < 32; i++) {
    if (v & (1 << i)) rv |= (1 << (31-i));
  }
  return rv;
}

unsigned int reverse(unsigned int v)
{
  int rv, i;

  rv = 0;
  for (i = 0; i < 32; i++) {
    rv <<= 1;
    rv |= (v & 1);
    v >>= 1;
  }
  return rv;
}

BTW, here's ChatGPT's answer:

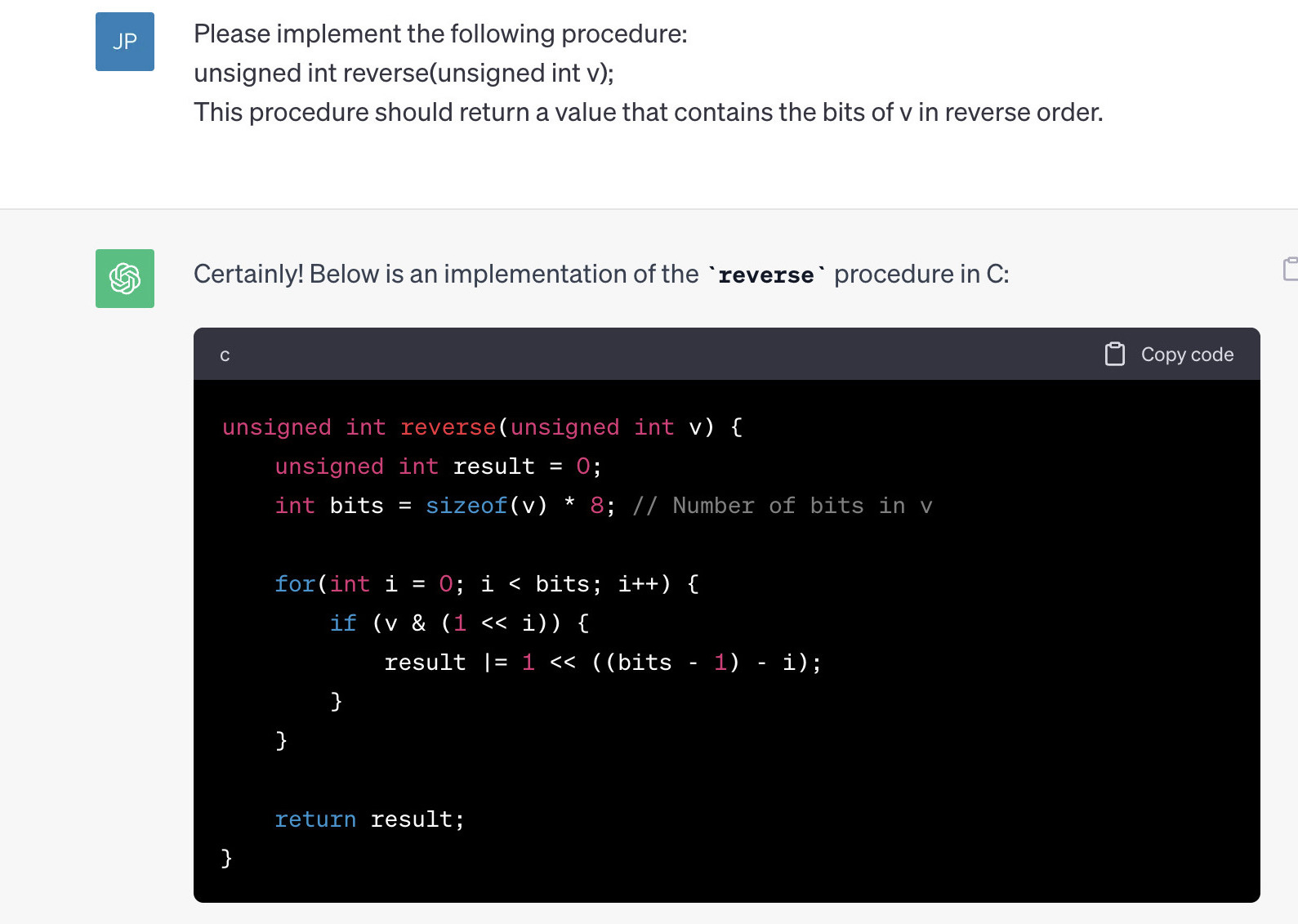I wish I could say that none of you used this answer in your answers, but I cannot say that :(.

Question 20: 15 points

The proper algorithm here is binary search. Find the index i where v[i][0] is < 0 and v[i+1][0] is ≥ 0. Then use the equation from the problem writeup to calculate the value.

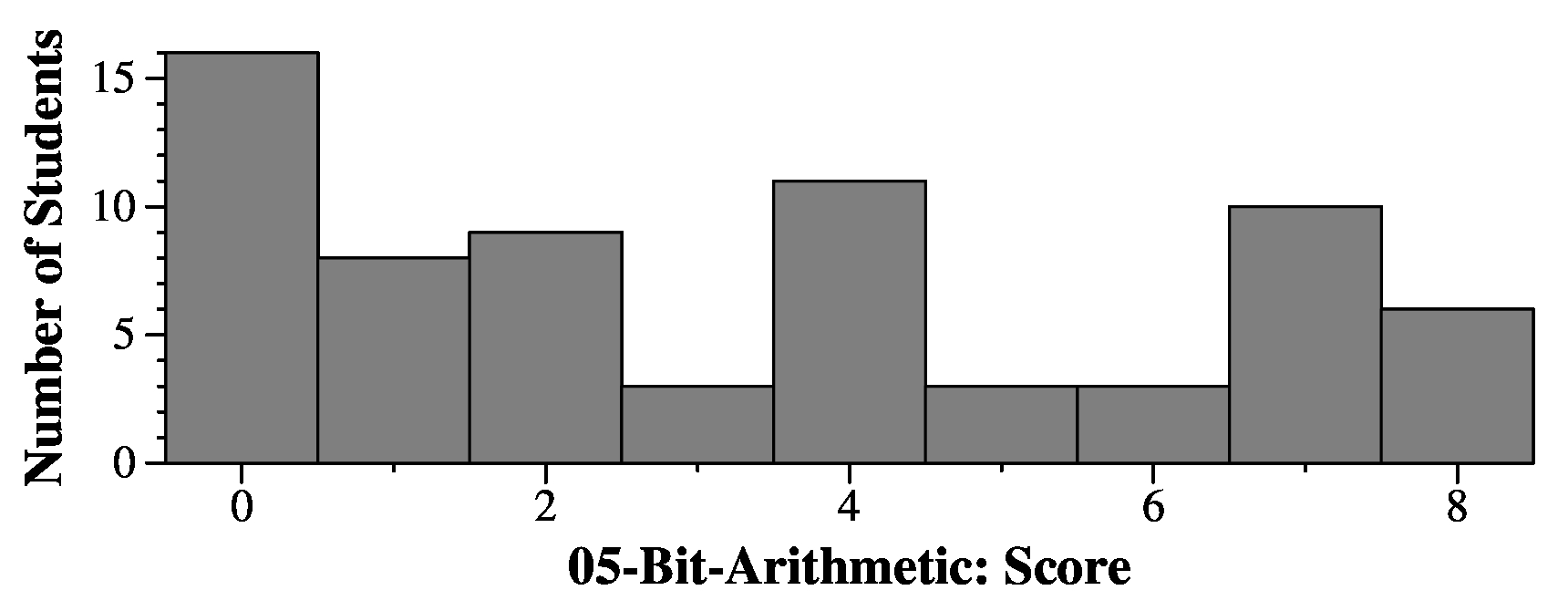Here is an answer that works with binary search:

double zero(const vector < vector <double> > &v)
{
  int start;
  int size;
  int mid;
  double x1, y1, x2, y2;

  start = 0;
  size = v.size();

  while (size > 1) {        /* The binary search is straight from the lecture notes. */
    mid = start + size/2;
    if (v[mid][0] < 0) {
      start = mid;
      size -= size/2;
    } else {
      size = size/2;
    }
  }
  
  x1 = v[start][0];
  y1 = v[start][1];
  x2 = v[start+1][0];
  y2 = v[start+1][1];

  return y1 - (x1 * (y2-y1) / (x2-x1));
}

The majority of you gave me an iterative solution, where you looped from 0 until you found the first positive number. That is a suboptimal algorithm, since it is O(n) rather than O(log n) as binary search is. With that solution, your maximum score was 8.

You'll note that ChatGPT doesn't use binary search, and it handles a case that the problem writeup says will not happen.

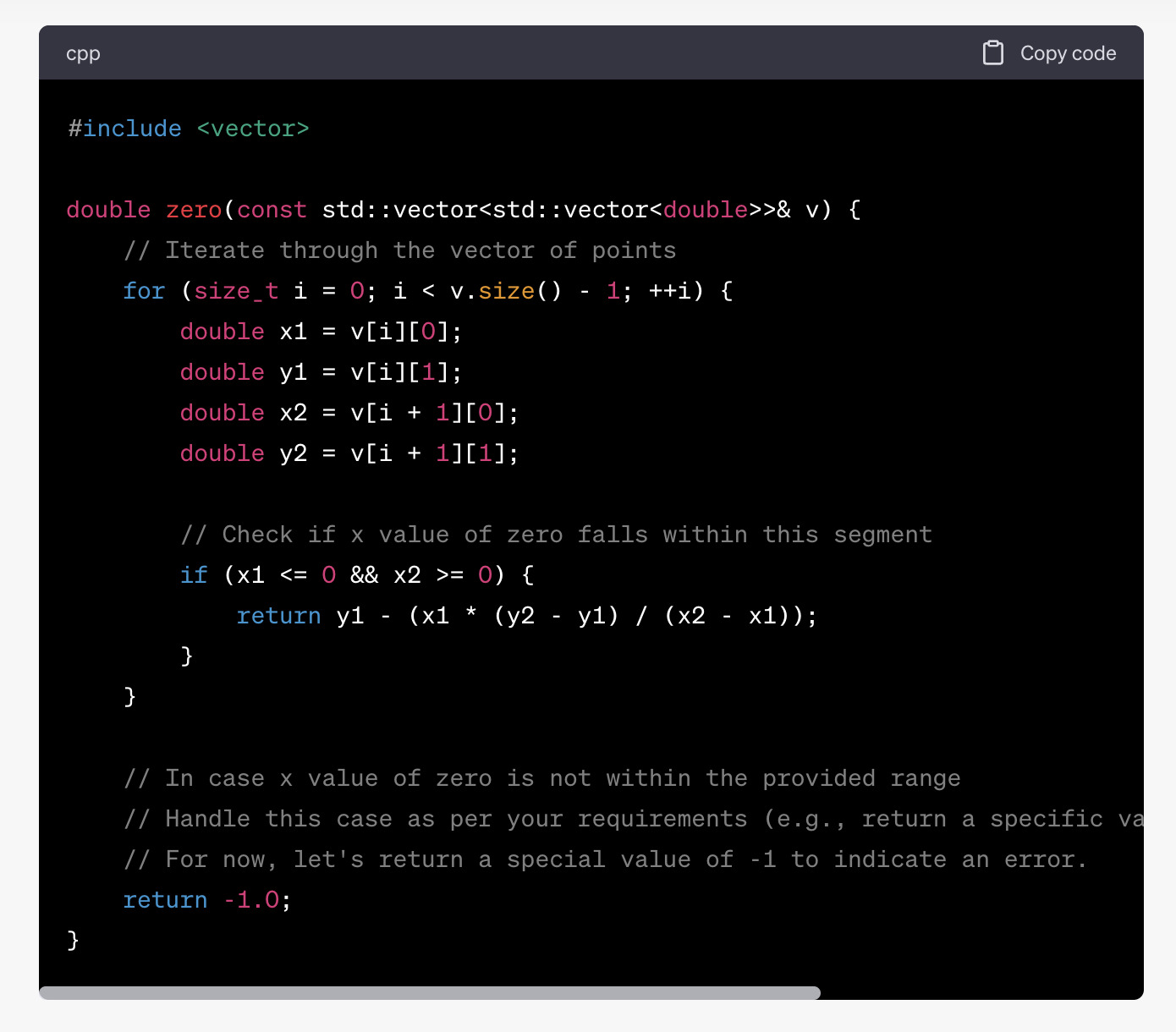I'm happy to report that no one used this solution, which would have received an 8.
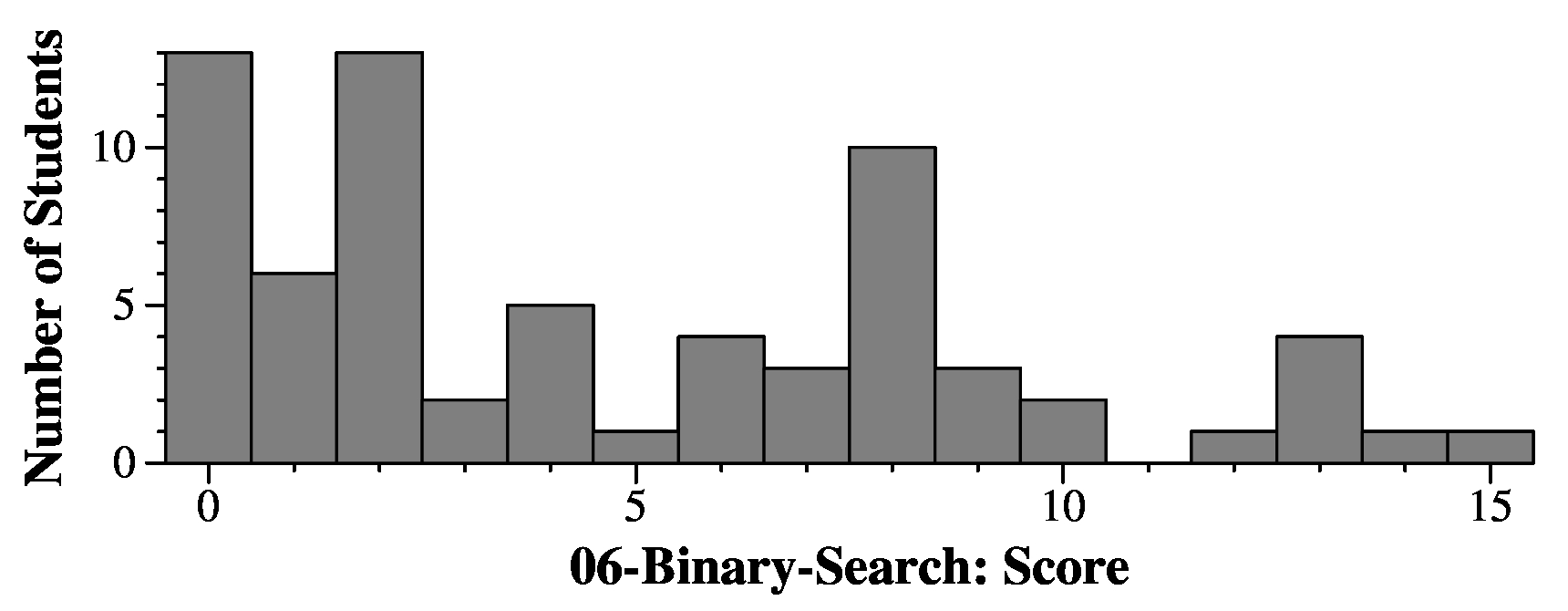