Question 1 (Six Points)
Part 1: What is the maximum flow of the graph to the right?(This is simply a number).
Part 2: What is the minimum cut of the graph to the right?
(This is not a number).
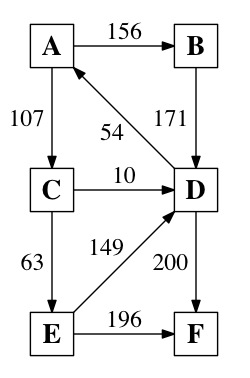 |
Question 1 (Six Points)Part 1: What is the maximum flow of the graph to the right?(This is simply a number).
Part 2: What is the minimum cut of the graph to the right?
|
|
|
(a): STL Sets and Maps.
(b): Insertion Sort. (c): Quicksort. (d): Bucket Sort (placing values in their approximate places and using insertion sort). (e): Depth-First Search. (f): Breadth-First Search on an Unweighted Graph. (g): Dijkstra's Algorithm. (h): Network Flow. (i): Minimum Spanning Tree. (j): Disjoint Sets. |
Problem 1: Finding the fastest driving route between two points, as in Mapquest or Yahoo maps.
Problem 2: Sorting 1,000,000 numbers uniformly distributed between 0 and 1.
Problem 3: Sorting 1,000,000 numbers distributed as an exponential whose mean is 3.500.
Problem 4: Sorting 1,000,000 numbers, where we have no idea about their distribution.
Problem 5: Determining the nodes in a graph reachable from a given node.
Problem 6: In Kruskal's algorithm, determining whether an edge connects two unconnected components.
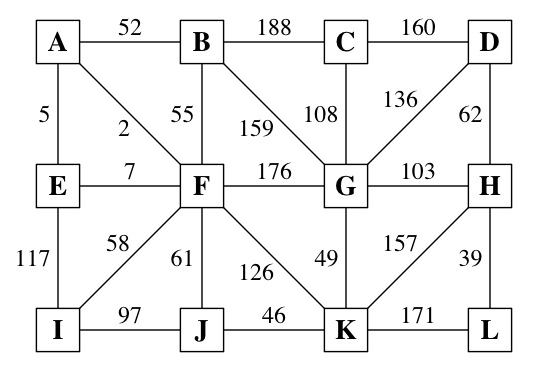 |
AF 2 AE 5 EF 7 HL 39 JK 46 GK 49 AB 52 BF 55 FI 58 FJ 61 DH 62 IJ 97 GH 103 CG 108 EI 117 FK 126 DG 136 HK 157 BG 159 CD 160 KL 171 FG 176 BC 188 |
Part 1: From the answers below, choose the one that shows the order in which edges are added to the Minimum Spanning Tree, using Kruskal's algorithm.
Part 2: From the answers below, choose the one that shows the order in which edges are added to the Minimum Spanning Tree, using Prim's algorithm.
If the algorithm requires a starting point, start from node A.
Answers: (Note, they are in alphabetical order, so you can find yours easily).
(a). AB, AE, AF, CG, DH, FI, FJ, GH, GK, HL, JK
(b). AF, AE, AB, BF, DH, EF, FI, FJ, GK, HL, JK
(c). AF, AE, AB, CG, DH, FI, FJ, GH, GK, HL, JK
(d). AF, AE, AB, FI, FJ, CG, DH, GH, GK, HL, JK
(e). AF, AE, AB, FI, FJ, JK, GK, GH, HL, DH, CG
(f). AF, AE, AB, HL, DH, JK, GK, GH, CG, FJ, FI
(g). AF, AE, DH, EF, AB, FJ, FI, JK, GK, BF, HL
(h). AF, AE, DH, EF, FI, HL, GK, BF, FJ, AB, JK
(i). AF, AE, DH, JK, HL, CG, GH, AB, FI, FJ, GK
(j). AF, AE, EF, HL, AB, BF, FI, DH, GK, JK, FJ
(k). AF, AE, EF, HL, JK, GK, AB, BF, FI, FJ, DH
(l). AF, AE, GH, JK, HL, AB, GK, FJ, CG, DH, FI
(m). AF, AE, HL, CG, AB, GK, DH, FJ, FI, GH, JK
(n). AF, AE, HL, JK, GK, AB, BF, FI, FJ, DH, GH
(o). AF, AE, HL, JK, GK, AB, FI, FJ, DH, GH, CG
|
This question concerns the directed graph to the right. For each of the
three augmenting path algorithms listed, state which of the answers gives
the first two augmenting paths for finding the network flow through the graph.
Included with each path is its flow, and that must be correct as well
(in other words, even though answers (a) and (b) have the same paths, they
specify different flows through the paths).
If an algorithm does not have a unique first two augmenting paths, simply give one answer that could result legally from that algorithm. For example, suppose both answers (a) and (e) could result as the first two paths of the Edmonds-Karp algorithm. Then either answer would be correct.
Part 1: The Edmonds-Karp algorithm. |
|
Answers
|
(a). ABCFBEFI (Flow 20), ADHFI (Flow 38). (b). ABCFBEFI (Flow 20), ADHFI (Flow 106). (c). ABCFBEFI (Flow 20), ADHI (Flow 26). (a). ABCFBEFI (Flow 20), ADHI (Flow 106). (e). ABCFI (Flow 82), ADHFI (Flow 24). (f). ABCFI (Flow 82), ADHFI (Flow 38). (g). ABCFI (Flow 82), ADHI (Flow 26). (h). ABCFI (Flow 147), ADHFI (Flow 24). (i). ABCFI (Flow 147), ADHFI (Flow 106). (j). ABCFI (Flow 147), ADHI (Flow 26). (k). ABCFI (Flow 147), ADHI (Flow 157). (l). ABEFI (Flow 20), ABCFI (Flow 38). (m). ABEFI (Flow 20), ADHFI (Flow 38). (n). ABEFI (Flow 20), ADHI (Flow 26). (o). ABEFI (Flow 179), ABCFI (Flow 147). |
(p). ABEFI (Flow 179), ADHFI (Flow 157). (q). ABEFI (Flow 179), ADHI (Flow 157). (r). ADBCFI (Flow 117), ABCFI (Flow 30). (s). ADBCFI (Flow 117), ABDFI (Flow 82). (t). ADGHI (Flow 138), ABCFI (Flow 147). (u). ADHFI (Flow 38), ABCFI (Flow 68). (v). ADHFI (Flow 38), ABCFI (Flow 82). (w). ADHFI (Flow 157), ABCFI (Flow 82). (x). ADHFI (Flow 157), ABCFI (Flow 147). (y). ADHI (Flow 26), ABEFI (Flow 20). (z). ADHI (Flow 26), ABFI (Flow 21). (1). ADHI (Flow 26), ADGHFI (Flow 38). (2). ADHI (Flow 26), ADGHFI (Flow 91). (3). ADHI (Flow 117), ABCFI (Flow 82). (4). ADHI (Flow 157), ABCFI (Flow 147). |
I have included work sheets for this question. Don't hand in the work sheet. Just the answer.
void insertion_sort(double *array, int size); int partition(double *array, int size, double value); |
insertion_sort() implements insertion sort.
partition() partitions an array, and works as follows: Suppose rv is the return value of a call to partition(). Then the first rv elements of array will contain values less than or equal to value, and the remaining (size-rv) elements of array will contain values greater than or equal to value.
Use these procedures to implement the fastest version of Quicksort that you can. And I mean the fastest. Don't be lazy - remember the sorting lecture and the things that make Quicksort run faster.
Here's the prototype:
void quick_sort(double *array, int size); |
Note, you are only to write quick_sort(). You are to assume that insertion_sort() and partition() are already written.
Question 6 (17 points)Behold the header file to the right:Implement the method Min_Hop_Path(), which finds the path from source to sink with the fewest number of hops. In other words, it finds the path that contains the fewest number of intermediate nodes. Obviously, if there is no path from source to sink, then it should return an empty list. You may assume that when Min_Hop_Path() is called, tmp equals zero for all nodes.
List routines to remember:
|
|
 |
AF 2 AE 5 EF 7 HL 39 JK 46 GK 49 AB 52 BF 55 FI 58 FJ 61 DH 62 IJ 97 GH 103 CG 108 EI 117 FK 126 DG 136 HK 157 BG 159 CD 160 KL 171 FG 176 BC 188 |
 |
AF 2 AE 5 EF 7 HL 39 JK 46 GK 49 AB 52 BF 55 FI 58 FJ 61 DH 62 IJ 97 GH 103 CG 108 EI 117 FK 126 DG 136 HK 157 BG 159 CD 160 KL 171 FG 176 BC 188 |
|
|