Question 1
- Part 1: The worst case running time of Quicksort is O(n2) while
Merge Sort is always O(n log(n)). A is faster.
- Part 2: DFS is O(n). Network Flow is much, slower, as each augmenting path
has to take at least
O(n). A is faster.
- Part 3: Unweighted shortest path is a simple BFS: O(n).
DFS is O(n). They are the same.
- Part 4:
Heap Sort is O(n log(n)). The worst (and average) case of Insertion sort
is O(n2). A is faster.
- Part 5: They are the same. Even though merge sort runs faster, their big-O complexity
is the same.
- Part 6:
Well, I had assumed that you knew the distribution of the data (or that the range of data is small)
so that bucket sort would be linear. However, if you don't know the distribution, bucket sort
defaults to insertion sort. That's a difficult one to analyze, so I gave full credit for any answer.
- Part 7:
Union operations are O(1). Find operations are O(α(n)), where α is
the inverse Ackerman function. So even though the inverse Ackerman of eight hundred bazillion is less than ten,
A is faster.
- Part 8:
Prim and Dijkstra's algorithms have the exact same mechanics -- they are both breadth-first searches
that grow a tree with an edge map. They are the same.
- Part 9:
Kruskal's algorithm has to sort the edges, so it is at least
O(n log(n)). Each Union operation is O(1), so n of them are O(n).
B is faster.
- Part A:
Heap Sort is O(n log(n)). Cycle detection is DFS, which is O(n): B is faster.
- Part B:
From part three -- A is O(n). Connected component determination is another DFS-based
algorithm. They are the same.
- Part C:
Matching on a bipartite graph is a network flow algorithm, which is way more expensive than
the O(n α(n)) operations required for n Find operations.
- Part D:
Both of these are linear: They are the same. Again, if you assumed that bucket sort didn't know
the distribution, then B would be faster, so I gave full credit for "B is faster".
- Part E:
Network flow is more expensive: B is faster. I gave .5 points for saying "A is faster", since
you may have considered that "Edmonds-Karp" meant finding the path and not the whole network
flow algorithm.
- Part F:
This is O(n), because it is ten iterations through an n element array.
Prim's algorithm is O(n log(n)). A is faster.
Grading
One point per part. I gave 0.2 points as partial credit for the following incorrect answers:
"Same" for Part 1. "B is faster" for Part 5. "Same" for Part 7.
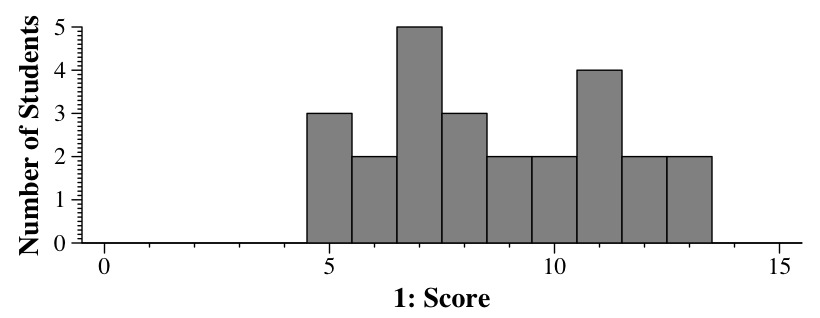
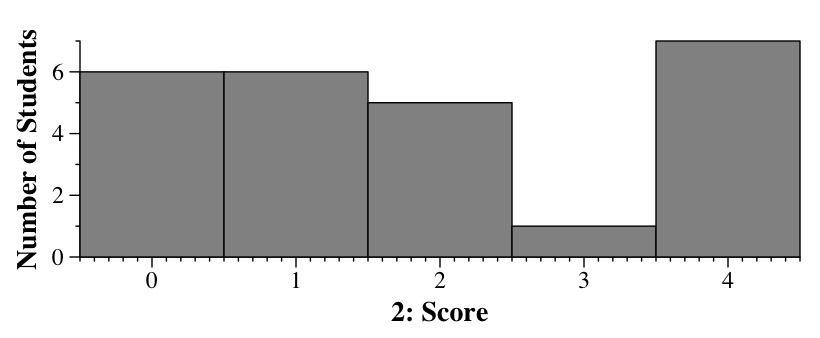
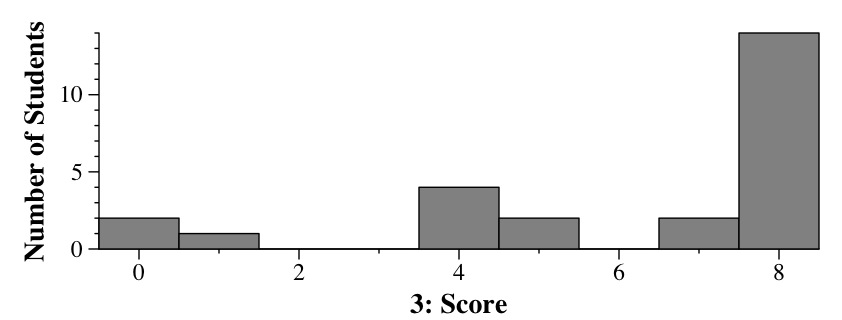
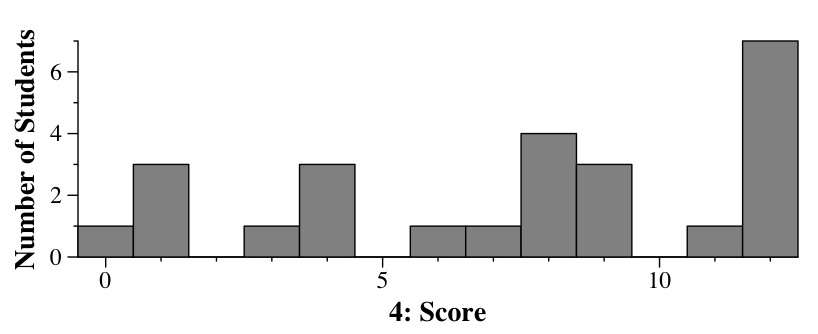
How Y'all Did
|
A |
B |
= |
| Part 1 |
5 |
3 |
17 |
| Part 2 |
19 |
4 |
2 |
| Part 3 |
3 |
6 |
16 |
| Part 4 |
21 |
1 |
3 |
| Part 5 |
1 |
9 |
13 |
| Part 6 |
17 |
6 |
1 |
| Part 7 |
15 |
6 |
4 |
| Part 8 |
12 |
7 |
6 |
| Part 9 |
6 |
14 |
5 |
| Part A |
11 |
12 |
2 |
| Part B |
5 |
7 |
13 |
| Part C |
15 |
7 |
3 |
| Part D |
4 |
10 |
11 |
| Part E |
4 |
15 |
5 |
| Part F |
8 |
15 |
2 |
Question 2
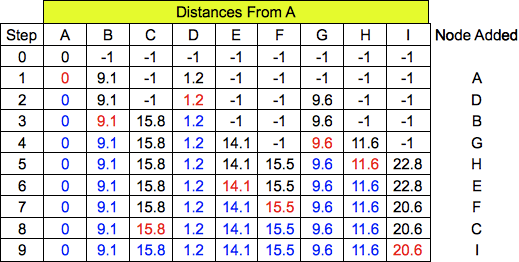
The answer is ADBGHEFCI. Here are the steps:
Grading
Four points -- I did give partial credit.
Question 3
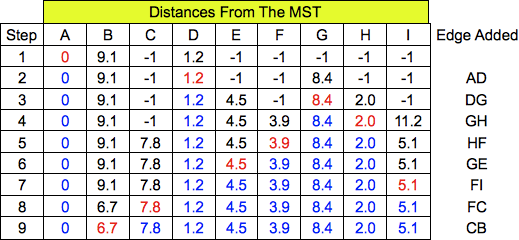
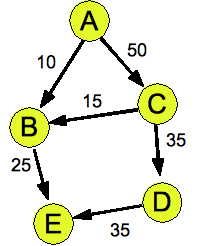
For Prim's algorithm, the answer is AD, DG, GH, HF, GE, FI, FC, CB. Prim's algorithm is a lot like
Dijkstra's algorithm -- here are the states at each step:
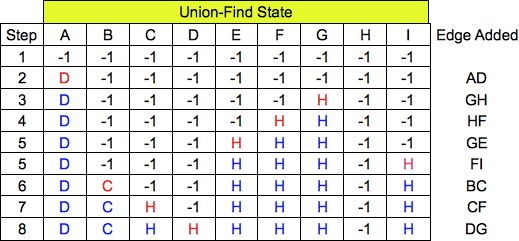
For Kruskal's algorithm, you first sort the edges, then use Union find to add edges to the MST.
If the edges connect nodes in different sets, then you add the edge to the tree and perform Union
on the two nodes' sets. Here are the states. The answer was a slow-pitch -- the first 8 edges in
their sorted order: AD, GH, HF, GE, FI, BC, CF, DG.
Grading
Four points each -- I did give partial credit.
Question 4
This is a simple BFS which uses a queue:
int Graph::Shortest_Path(Node *a, Node *b)
{
int i;
list <Node *> bfsq;
list <Node *>::iterator bit;
Node *n;
for (i = 0; i < nodes.size(); i++) nodes[i]->tmp = -1;
a->tmp = 0;
bfsq.push_back(a);
while (!bfsq.empty()) {
bit = bfsq.begin();
n = *bit;
bfsq.erase(bit);
if (n == b) return n->tmp;
for (i = 0; i < n->edges.size(); i++) {
if (n->edges[i]->tmp == -1) {
n->edges[i]->tmp = n->tmp+1;
bfsq.push_back(n->edges[i]);
}
}
}
return -1;
}
|
To test this, I hacked up a little main() which first creates a ten-node graph where node i has an
edge to node i+1. It then prints out the path distance from node 0 to node 9 (which should be 9) and
the path from node 9 to node 0 (which should be -1).
Then, for each node i I add edges to every node j such that j < i, and print out
the same path lengths. Node 0 to node 9 should still have a path length of 9. Node 9 to node 0 should
have a path length of 1. The code is in
bfs.cpp
main()
{
Graph g;
Node *n;
int i, j;
for (i = 0; i < 10; i++) {
n = new Node;
g.nodes.push_back(n);
}
for (i = 0; i < 9; i++) {
g.nodes[i]->edges.push_back(g.nodes[i+1]);
}
cout << g.Shortest_Path(g.nodes[0], g.nodes[9]) << endl;
cout << g.Shortest_Path(g.nodes[9], g.nodes[0]) << endl;
for (i = 0; i < 10; i++) {
for (j = 0; j < i; j++) {
g.nodes[i]->edges.push_back(g.nodes[j]);
}
}
cout << g.Shortest_Path(g.nodes[0], g.nodes[9]) << endl;
cout << g.Shortest_Path(g.nodes[9], g.nodes[0]) << endl;
}
|
UNIX> bfs
9
-1
9
1
UNIX>
Grading
Basically, you started at a certain maximum value, depending on how you structured your code.
These values were:
- Excellent/Good: A correct structure based on a BFSQ: 12 points
- Recursive structure that gave a correct answer: 9 points
- Used a BFSQ, but not well: 6 points
- No BFSQ/Just looping through a, incorrect recursive structure: 4 points.
After that, there were the following deductions:
- Needs a separate BFSQ -- you used nodes instead: 3 points.
- Lots of confused stuff going on: 3 points -- this was if you had too much nonsensical code.
- Length Calculated Incorrectly: 3 points -- this wasn't minor -- if you had this deduction, you
were not using the tmp field to calculate the shortest path, which means that you weren't using BFS
correctly.
- Too much incorrect syntax: 2 points -- similar to "confused stuff" above, but not as major.
- Returns 0 when there's no path: 1 point.
- Don't set tmp for any nodes: 1 points
Question 5
Re-read the lecture notes if you don't understand any of these answers.
- The maximum flow is 60. Here is a flow graph:
- From the flow graph, it is easy to see that the minimum cut is composed of the edges BE and DE.
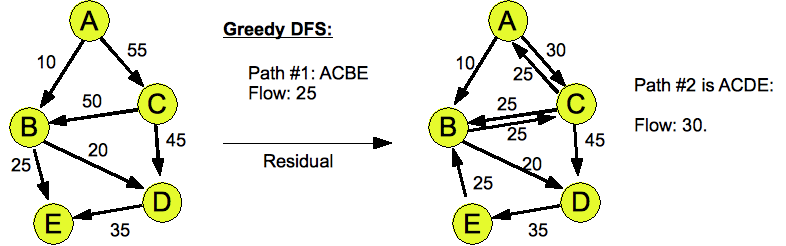
- Here are the answers for Greedy DFS:
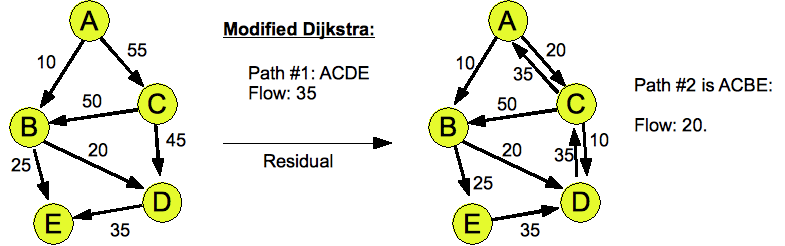
- Here are the answers for Modified Dijkstra:
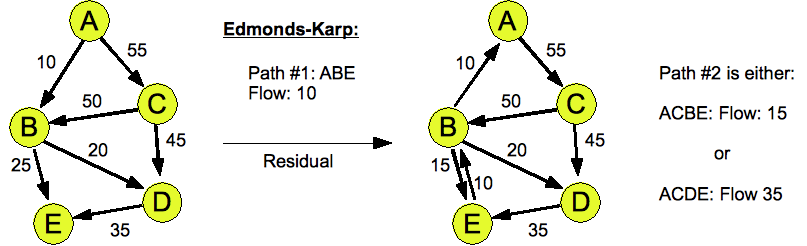
- Here are the answers for Edmonds-Karp:
Grading
One point for each of the 11 parts. I gave credit for the proper residual graph for your answer, even if your answer was wrong.
Question 6
The recursive definition maps directly to a recursive function. Simply use a cache to memoize it
(This is in q4.cpp):
double CalcX::X(int x, int y)
{
int i;
double retval, tmp;
// Set up the cache if need be.
if (cache.size() < x+1) {
cache.resize(x+1);
for (i = 0; i <= x; i++) {
if (cache[i].size() < y+1) cache[i].resize(y+1, -1);
}
}
// Return the value from the cache if it is there.
if (cache[x][y] != -1) return cache[x][y];
// Otherwise, do the recursive calculation
retval = 0;
if (x == 0 && y == 0) retval = 1;
if (x > 0) {
tmp = F1(x-1, y);
if (tmp > retval) retval = tmp;
}
if (y > 0) {
tmp = F2(x, y-1);
if (tmp > retval) retval = tmp;
}
// Put it into the cache and return
cache[x][y] = retval;
return retval;
}
|
Grading
As with Question 4, you started at a certain maximum value, depending on how you structured your code.
These values were:
- Excellent/Good: 12 points
- Zero: 0 points
After that, there were the following deductions:
- Dynamic program without a cache: 4 points. This was major, because setting up the cache was an
important part of the program.
- Uses a for loop to build the cache without recursion: 3 points. This was also major -- yes, you
can structure this as a doubly-nested for loop, but the question said to make it recursive with a cache.
- Cache not used as a vector, but some weird associative array: 3 points.
- Weird recursion -- set the cache for x,y-1 and y,x-1, never for x,y.: 2 points. These worked correctly,
but will perform a factor of two worse than doing it the right way (as in the answer above).
- Both loops and recursion -- performance is going to be terrible: 2 points.
- Never-Check-Cache: 2 points. This i when you never use the cache.
- Don't deal with X(0,y) or X(y,0) correctly. : 2 points. A lot of you got this deduction, and many of you
got it because you returned -1 when x or y was less than zero. Then you made a recursive call and didn't check that
you were calling with a negative value, and certainly having it return -1 isn't going to eliminate that case.
If you just said "negative infinity", I counted it as ok. I said that I don't care what you return when x or y is
negative, which is true -- I do care that you get the correct values when x or y is equal to zero, which many of
you failed to do.
- Don't Set Cache On Return: 2 points. This is when you forgot to set the value in the cache when you returned
from the procedure.
- Confused resizing of the cache: 2 points.
- Use Cache Before Resize : 1 point.
- The cache is too small: only resize to x and y: 1 point. The cache needs to be resized to x+1 and y+1.
- Forgot about x == 0 & y == 0 or got it wrong: 1 point.
- Cache never initialized: 1 point.